- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Введени е в астрономию
Содержание
- 4. Первобытный философ не проводил экспериментов, он созерцал
- 5. движутся Солнце и Луна, и множество Звездсветят
- 6. а над Океаном опрокинуто Небо, как некая
- 7. полусферой, в которую вкрапленыЗвезды. Но дальнейшие его
- 8. Звезды также продолжают быть вкрапленными в Небесную
- 9. Столь оригинальное представление о Большом мире, сформировавшееся
- 10. Центр ее в зависимости от решаемой задачи
- 11. Но, введя в обиход понятие “Небесная сфера”,
- 12. О перемещении Солнца можно было судить по
- 13. И для реализации столь грандиозного замысла люди
- 14. Выбор направлений отсчета.Положение точки в пространстве можно
- 15. Все происходящее во внешнем мире, мы воспринимаем
- 16. Представление о сферичности внешнего мира на прямую
- 17. Отвесная линияДругое чувство – чувство равновесия
- 18. Отвесная линияПроконтролировать направление “ВЕРХ – НИЗ”
- 19. Плоскость математического горизонтаВторое базовое направление должно
- 20. Плоскость математического горизонтаЛиния второго базового направления,
- 21. Эту плоскость мы представляем лишь в своем
- 22. Плоскость математического горизонта Итак, плоскость, перпендикулярную
- 23. Направление Восток – Запад. Естественная смена дня
- 24. Восход Солнца. Но давайте внимательно понаблюдаем за
- 25. Движение Солнца по небу. Теперь проследим за
- 26. Движение Солнца по небуУТРОВыйдя из-за горизонта, Солнце
- 27. Движение Солнца по небуДЕНЬ. В какой-то момент
- 28. Движение Солнца по небуВЕЧЕРСолнце уже близко к
- 29. Движение Солнца по небуТочно так же, как
- 30. Но наиболее важно то, что внимательный наблюдатель
- 31. ГномонНо это только предположение, и его надо
- 32. ГномонЭтот метод опирается на свойство предметов отбрасывать
- 33. ГномонПо тени, отбрасываемой гномоном, можно судить о
- 34. Полуденная линияНаблюдая за траекторией движения тени гномона,
- 35. Полуденная линияАргументировал он это тем, что направление,
- 36. Горизонтальная система координат Небесная сфера, центр которой
- 37. Плоскость математического горизонта. Плоскость математического горизонта –
- 38. Плоскость математического горизонта. Линия пересечения сферы плоскостью
- 39. Горизонтальная система координат Линия Восток – Запад.
- 40. Горизонтальная система координат Линия Восток – Запад.
- 41. Если продолжить линию Восток - Запад до
- 42. Плоскость меридианаЧерез отвесную линию и полуденную линию
- 43. Плоскость Первого вертикалаЧерез отвесную линию и
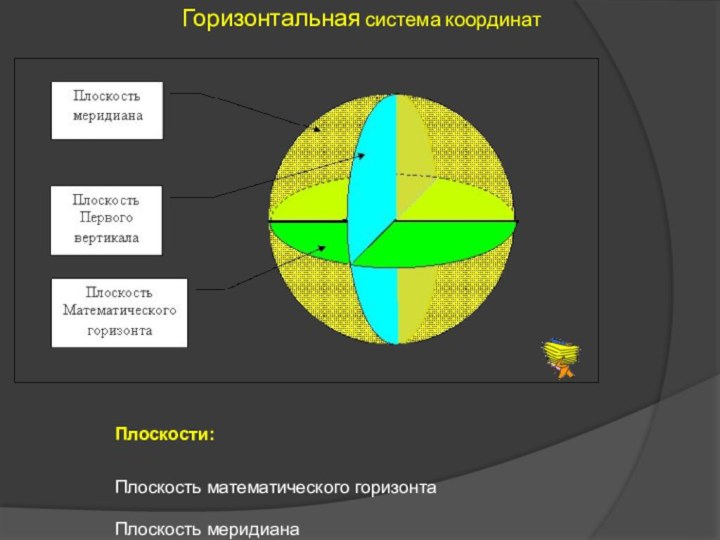
- 44. Горизонтальная система координатПлоскости: a. Плоскость математического горизонта b. Плоскость меридиана
- 45. Горизонтальная система координатЛинииПолуденная линия Отвесная линия Линия Восток Запад
- 46. Горизонтальная система координатПлоскости: Плоскость математического горизонта Плоскость меридиана
- 47. ТочкиТочка отсчета, она же – центр Небесной
- 48. Скачать презентацию
- 49. Похожие презентации



































Слайд 4
Первобытный философ не
проводил экспериментов,
он созерцал окружающий
его мир,
него недоумение
Слайд 5
движутся Солнце и Луна, и множество Звезд
светят ночью,
и ничто из них не собирается
падать.
Правда, некоторые звезды
все же падают,оставляя за собой яркий след. И первобытный
философ попытался объяснить это.
Он знал, что, если выронить какой-нибудь
предмет из рук, то этот предмет всегда
падает вниз, но он видел, что, по
непонятным для него причинам, над ним
Слайд 6 а над Океаном опрокинуто Небо, как некая хрустальная
полусфера, в которую вкраплены Звезды. На этой полусфере есть
дорога, по которой движутся Солнце, Луна и некоторые Звезды, которые он назвал Планетами.Пути Солнца, Луны и Планет – называются траекториями движения.
И у него все выглядело просто и логично –
Земля окружена Океаном,
Слайд 7
полусферой, в которую вкраплены
Звезды. Но дальнейшие его созерцания
указали
ему на его заблуждение. Он
заметил, что и Звезды перемещаются
по
небу – медленно, но все жедостаточно для того, чтобы это заметить.
И тогда философ пересматривает свои
выводы.
Итак, наш философ пришел к выводу, что Земля накрыта неподвижной хрустальной
Слайд 8 Звезды также продолжают быть вкрапленными в Небесную сферу
и движутся вместе с ней. Размеры Небесной сферы, считал
наш философ, настолько огромны, что этого даже нельзя себе вообразитьТеперь у него Земля окружена сферой, которую он назвал Небесной сферой, и эта Небесная сфера вращается вокруг Земли.
Слайд 9 Столь оригинальное представление о Большом мире, сформировавшееся у
древнего философа, было, как видно, настолько удачным, что оно
дошло и до наших дней. С некоторыми изменениями и мы пользуемся понятием “Небесная сфера”.Слайд 10 Центр ее в зависимости от решаемой задачи совмещают
с той или иной точкой пространства.
В частности, о
видимой нами небесной сфере можно сказать, что это воображаемая сфера сколь угодно большого радиуса, в центре которой находится глаз наблюдателя Дадим определение этому понятию:
Небесная сфера – это воображаемая сфера произвольного радиуса.
Слайд 11 Но, введя в обиход понятие “Небесная сфера”, наш
философ столкнулся с очередной трудностью, которую он пока что
не мог разрешить.Если принять за основу понятие о небесной сфере, то получается, что Солнце, Луна и Планеты должны были бы быть так же прикреплены к ней, однако наш наблюдатель отчетливо видел, особенно это касалось Луны, что каждую ночь Луна, например, появляется вблизи различных звезд. При более настойчивых наблюдениях, это можно было сказать и о Планетах.
Слайд 12 О перемещении Солнца можно было судить по косвенным
признакам. Значит, сказал философ, надо попробовать определить закономерности в
движении этих светил, иначе представление о Мире у нас будет не полным.Слайд 13 И для реализации столь грандиозного замысла люди начали
вести систематические наблюдения за движением Солнца, Луны и Планет
среди Звезд. Но чтобы эти наблюдения не пропадали даром и были понятны другим наблюдателям, ученые договорились о способах фиксации увиденного или, другими словами, были определены:Единицы, в которых проводились измерения положения светил.
Системы отсчета, относительно которых проводились измерения.
Слайд 14
Выбор направлений отсчета.
Положение точки в пространстве можно однозначно
определить, используя только ДВЕ координаты, если считать, что эта
точка располагается на поверхности СФЕРЫ фиксированного радиуса. Эти координаты представляют собой дуги больших кругов и измеряются величиной центральных углов между направлением на точку пространства и ДВУМЯ, заранее выбранными БАЗОВЫМИ направлениями.Слайд 15 Все происходящее во внешнем мире, мы воспринимаем через
ВРОЖДЕННЫЕ чувства или, через ЧУВСТВЕННЫЙ ОПЫТ. Одним из врожденных
чувств является ЗРЕНИЕ. Посмотрите ночью на ясное небо. Каким оно Вам покажется? А покажется оно нам опрокинутой полусферой со множеством светящихся объектов. Но попытайтесь определить, который из объектов к нам ближе, а какой дальше. Ваши усилия ни к чему не приведут.Эти объекты будут казаться равноудаленными от нас.
Слайд 16 Представление о сферичности внешнего мира на прямую связано
со строением наших органов зрения.
Мир - сферичен, что
все небесные объекты вкраплены в эту сферу, а раз это так, то положение небесных объектов можно однозначно определить, если мы определим всего лишь ДВА БАЗОВЫХ направления, относительно которых и будут отсчитываться координаты небесных объектов
Слайд 17
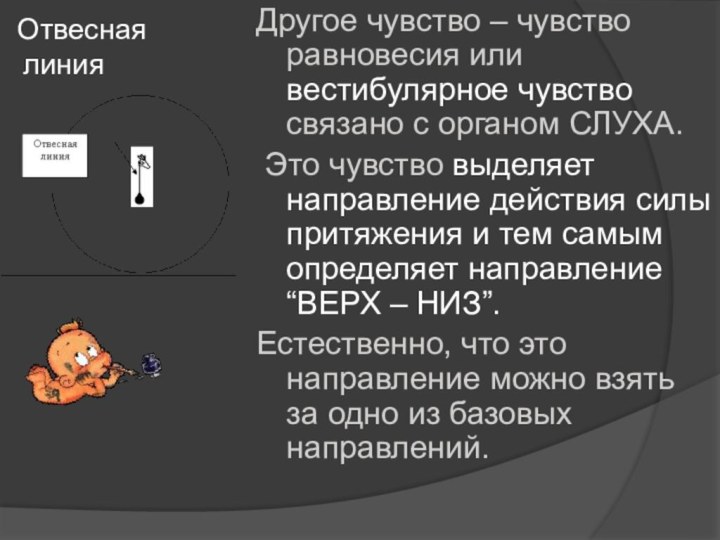
Отвесная
линия
Другое чувство – чувство равновесия или вестибулярное
чувство связано с органом СЛУХА.
Это чувство выделяет направление
действия силы притяжения и тем самым определяет направление “ВЕРХ – НИЗ”. Естественно, что это направление можно взять за одно из базовых направлений.
Слайд 18
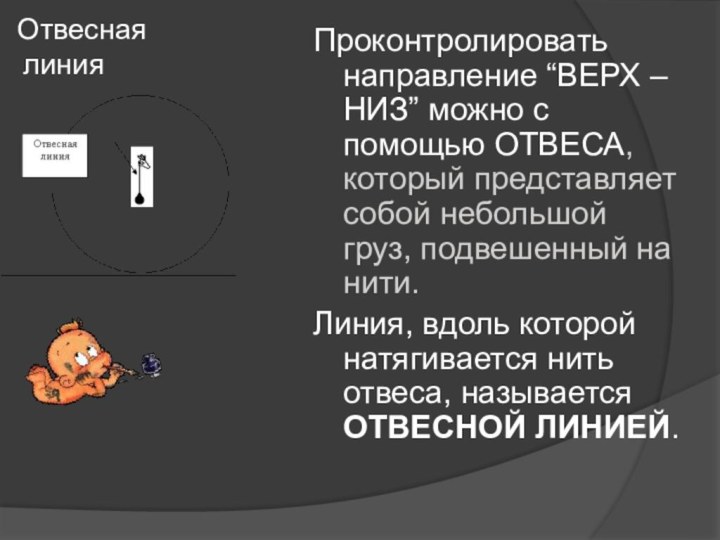
Отвесная
линия
Проконтролировать направление “ВЕРХ – НИЗ” можно с
помощью ОТВЕСА, который представляет собой небольшой груз, подвешенный на
нити.Линия, вдоль которой натягивается нить отвеса, называется ОТВЕСНОЙ ЛИНИЕЙ.
Слайд 19
Плоскость математического горизонта
Второе базовое направление должно быть ПЕРПЕНДИКУЛЯРНО
отвесной линии, следовательно, некоторая линия, отображающее это базовое направление,
должна находиться в плоскости, перпендикулярной отвесной линии.
Слайд 20
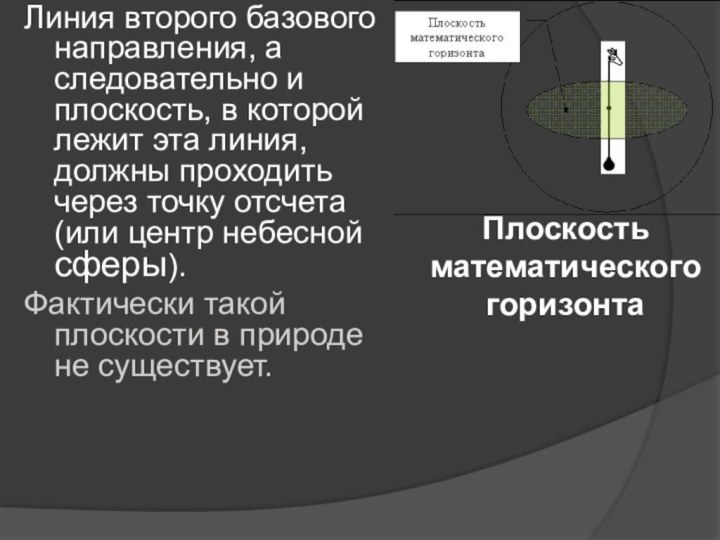
Плоскость математического горизонта
Линия второго базового направления, а следовательно
и плоскость, в которой лежит эта линия, должны проходить
через точку отсчета (или центр небесной сферы).Фактически такой плоскости в природе не существует.
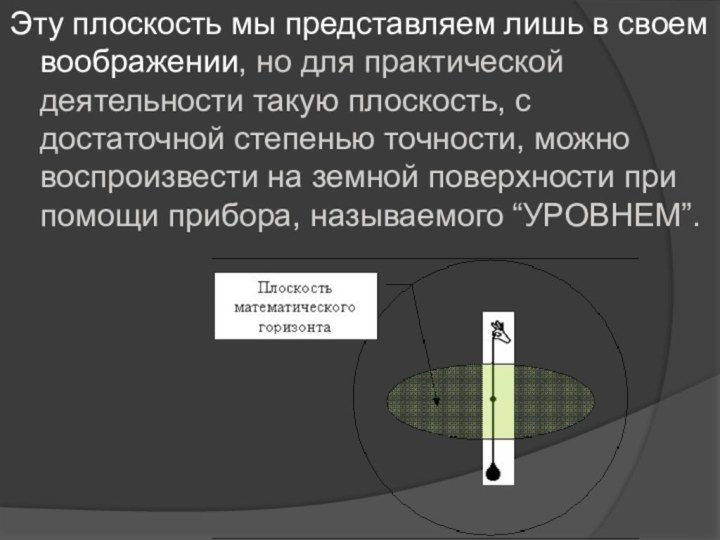
Слайд 21 Эту плоскость мы представляем лишь в своем воображении,
но для практической деятельности такую плоскость, с достаточной степенью
точности, можно воспроизвести на земной поверхности при помощи прибора, называемого “УРОВНЕМ”.
Слайд 22
Плоскость математического горизонта
Итак, плоскость, перпендикулярную отвесной линии,
мы будем называть ПЛОСКОСТЬЮ МАТЕМАТИЧЕСКОГО ГОРИЗОНТА.
Определившись с плоскостью,
в которой должна находиться линия второго базового направления, приступим к отысканию этого самого направления.
Слайд 23
Направление Восток – Запад
. Естественная смена дня и
ночи определяет направление Восток – Запад. Появляется мысль, что
это направление и можно взять за второе базовое направление, то есть определить направление из точки наблюдения на точку восхода Солнца. Кстати сказать. На латинском языке слово “ВОСТОК” звучит, как “ОРИЕНС”. Отсюда произошло понятие и слово “ОРИЕНТАЦИЯ”
Слайд 24
Восход Солнца
. Но давайте внимательно понаблюдаем за восходом
Солнца и попытаемся определить точку восхода. Мы, к своему
сожалению, убедимся, что точка восхода передвигается вдоль горизонта. И, если бы мы выбрали базовое направление на точку восхода, то это привело бы к неопределенности.
Слайд 25
Движение Солнца по небу
. Теперь проследим за движением
Солнца по небу. В любой день, но тогда, когда
небо ясное, мы увидим привычную для нас картинку.
Слайд 26
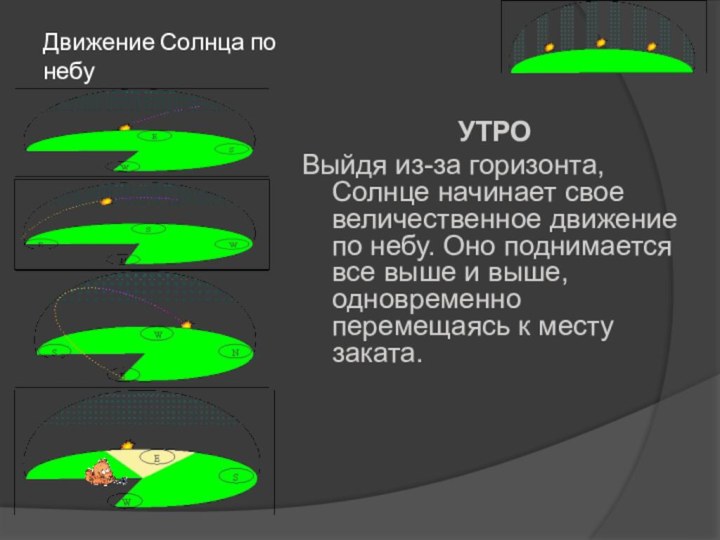
Движение Солнца по небу
УТРО
Выйдя из-за горизонта, Солнце начинает
свое величественное движение по небу. Оно поднимается все выше
и выше, одновременно перемещаясь к месту заката.
Слайд 27
Движение Солнца по небу
ДЕНЬ.
В какой-то момент Солнце
занимает наивысшее для этого дня положение на небе. Этот
момент мы называем ПОЛДНЕМ. Миновав полдень, Солнце начинает опускаться, продолжая движение к месту заката
Слайд 28
Движение Солнца по небу
ВЕЧЕР
Солнце уже близко к горизонту.
Вот оно уже коснулось своим краем этой недостижимой линии.
Ещё немножко и диск Солнца плавно скрывается за ней. Внимательный наблюдатель заметит, что и закат Солнца в разные дни происходит в различных местах.
Слайд 29
Движение Солнца по небу
Точно так же, как точка
восхода день ото дня, меняет своё положение, точка заката
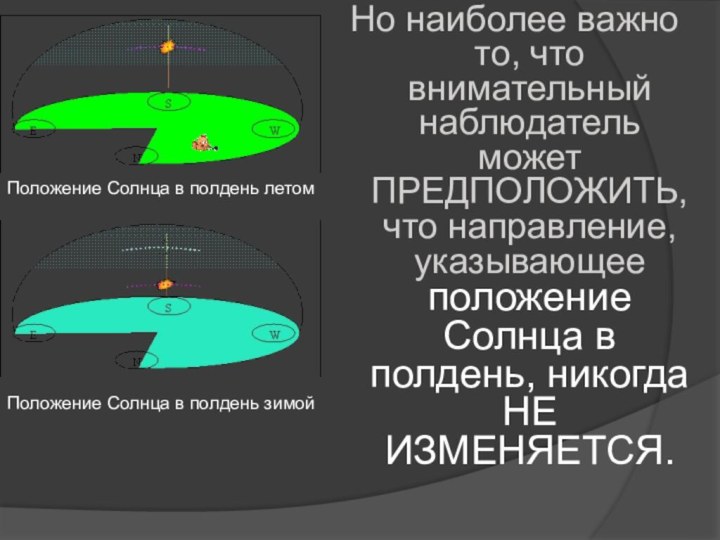
не остается на одном и том же месте. Ещё внимательный наблюдатель отметит у себя и то, что, хотя точка восхода и захода перемещаются вдоль линии горизонта, но они никогда на выходят за границы некоторого сектора).Слайд 30 Но наиболее важно то, что внимательный наблюдатель может
ПРЕДПОЛОЖИТЬ, что направление, указывающее положение Солнца в полдень, никогда
НЕ ИЗМЕНЯЕТСЯ.Положение Солнца в полдень летом
Положение Солнца в полдень зимой
Слайд 31
Гномон
Но это только предположение, и его надо либо
подтвердить, либо опровергнуть, а для этого необходимо определить траекторию
движения Солнца в различные дни, а затем сравнить результаты этих наблюдений.Непосредственно наблюдать за движением Солнца у нас нет никакой возможности из-за того, что Солнце нас просто-напросто ослепит, и тогда был предложен метод косвенного наблюдения.
Слайд 32
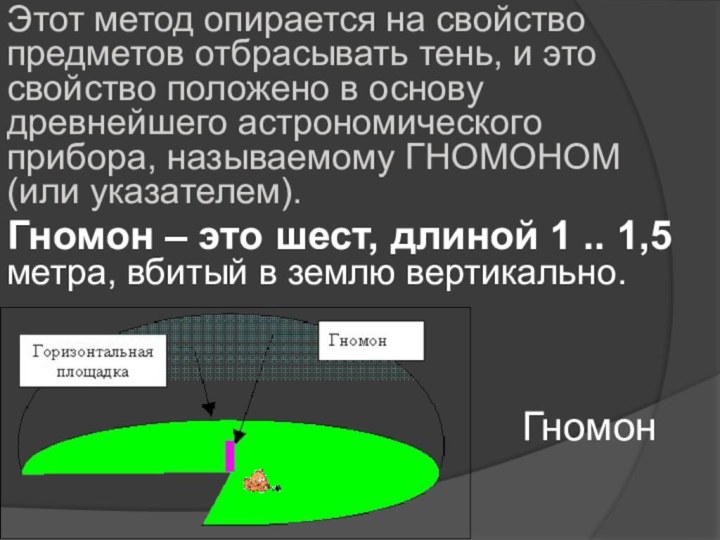
Гномон
Этот метод опирается на свойство предметов отбрасывать тень,
и это свойство положено в основу древнейшего астрономического прибора,
называемому ГНОМОНОМ (или указателем).Гномон – это шест, длиной 1 .. 1,5 метра, вбитый в землю вертикально.
Слайд 33
Гномон
По тени, отбрасываемой гномоном, можно судить о положении
Солнца на небе. Следует, однако, учесть очень важный момент
- при определении положения Солнца на небе, тень от гномона должна падать на ГОРИЗОНТАЛЬНУЮ площадку.Если немножко подумать, то эту горизонтальную площадку мы можем ассоциировать с ПЛОСКОСТЬЮ МАТЕМАТИЧЕСКОГО ГОРИЗОНТА, а сам гномон – с ОТВЕСНОЙ ЛИНИЕЙ
Слайд 34
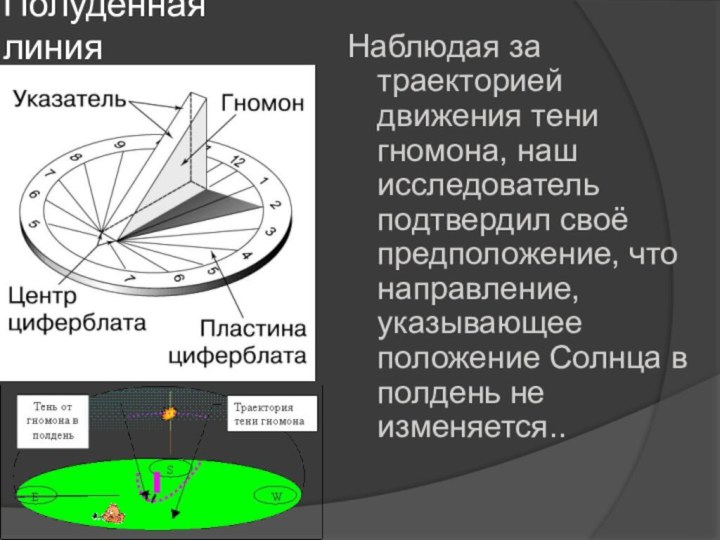
Полуденная линия
Наблюдая за траекторией движения тени гномона, наш
исследователь подтвердил своё предположение, что направление, указывающее положение Солнца
в полдень не изменяется..
Слайд 35
Полуденная линия
Аргументировал он это тем, что направление, по
которому отбрасывается тень гномона в полдень, всегда ОДНО И
ТОЖЕ, хотя, как мы понимаем, длина тени в различные дни будет не одинаковой.Полученное направление носит название ПОЛУДЕННОЙ ЛИНИИ, и оно принято за ВТОРОЕ БАЗОВОЕ НАПРАВЛЕНИЕ.
Слайд 36
Горизонтальная система координат
Небесная сфера, центр которой является
точкой наблюдения. Отвесная линия, проходящая через центр небесной сферы
(или точку наблюдения).Если продолжить отвесную линию до пересечения ею небесной сферы, то мы получим две точки –
одна из которых будет находиться прямо над нами, другая – прямо под нами.
Точка, находящаяся прямо над нами, называется точкой ЗЕНИТА (обозначается как Z).
Точка, находящаяся прямо под нами, называется точкой НАДИРА (обозначается как Na)
Слайд 37
Плоскость математического горизонта.
Плоскость математического горизонта – плоскость
перпендикулярная отвесной линии и пересекающая её в точке наблюдения
(или центре небесной сферы).Плоскость математического горизонта разделяет сферу на два полушария – СЕВЕРНОЕ и ЮЖНОЕ.
Слайд 38
Плоскость математического горизонта.
Линия пересечения сферы плоскостью математического
горизонта называется ЛИНИЕЙ МАТЕМАТИЧЕСКОГО ГОРИЗОНТА
или просто
МАТЕМАТИЧЕСКИМ ГОРИЗОНТОМ.
Слайд 39
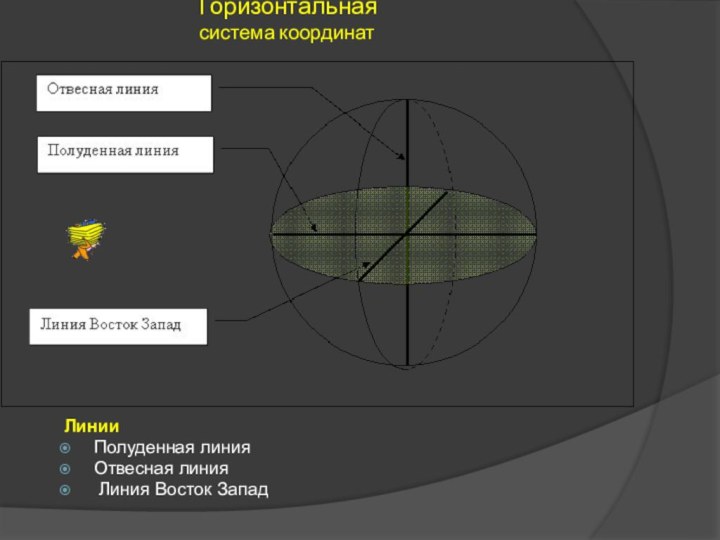
Горизонтальная система координат
Линия Восток – Запад.
Но для
лучшего восприятия этой системы координат, сделаем ряд вспомогательных построений.
Проведем в плоскости математического горизонта через точку отсчета линию, перпендикулярную полуденной линии.
Эта линия носит название ЛИНИИ ВОСТОК – ЗАПАД.
Слайд 40
Горизонтальная система координат
Линия Восток – Запад.
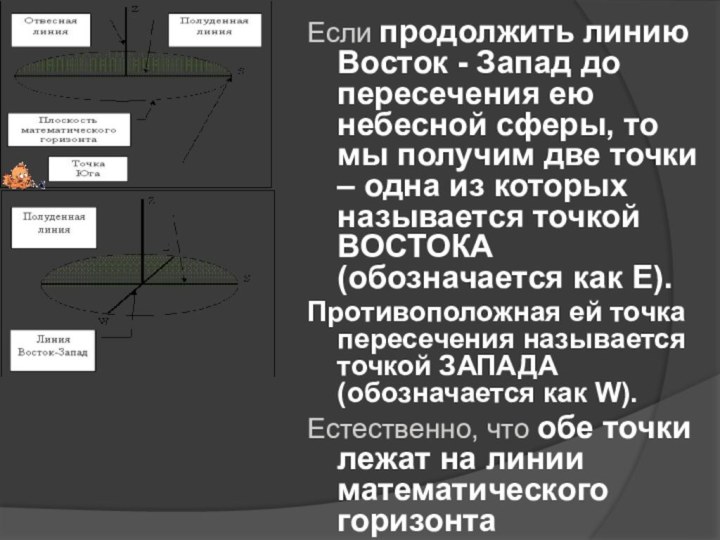
Фактически, определив
два базовых направления – отвесную линию и полуденную линию,
мы создали систему отсчета, называемую Горизонтальной системой координат.Слайд 41 Если продолжить линию Восток - Запад до пересечения
ею небесной сферы, то мы получим две точки –
одна из которых называется точкой ВОСТОКА (обозначается как Е).Противоположная ей точка пересечения называется точкой ЗАПАДА (обозначается как W).
Естественно, что обе точки лежат на линии математического горизонта
Слайд 42
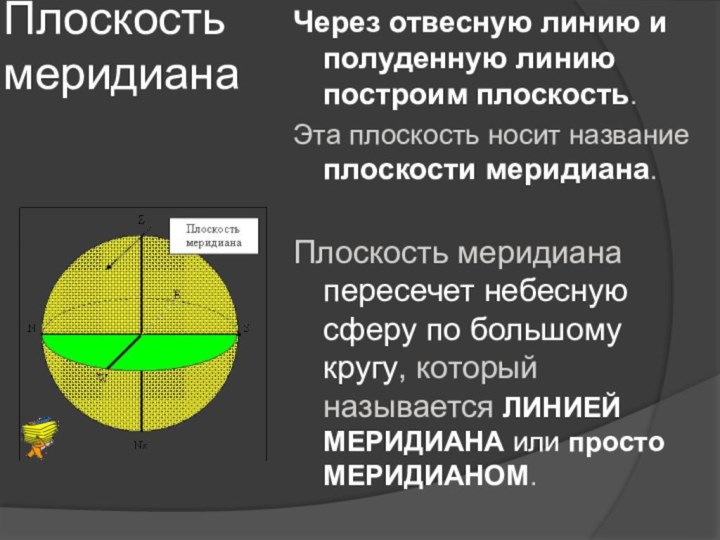
Плоскость меридиана
Через отвесную линию и полуденную линию построим
плоскость.
Эта плоскость носит название плоскости меридиана.
Плоскость меридиана
пересечет небесную сферу по большому кругу, который называется ЛИНИЕЙ МЕРИДИАНА или просто МЕРИДИАНОМ.
Слайд 43
Плоскость
Первого вертикала
Через отвесную линию и линию ВОСТОК
_ ЗАПАД построим плоскость.
Эта плоскость носит название плоскости
Первого вертикала. Плоскость Первого Вертикала пересечет небесную сферу по большому кругу, который называется
ЛИНИЕЙ ПЕРВОГО ВЕРТИКАЛА или просто ПЕРВЫМ ВЕРТИКАЛОМ.
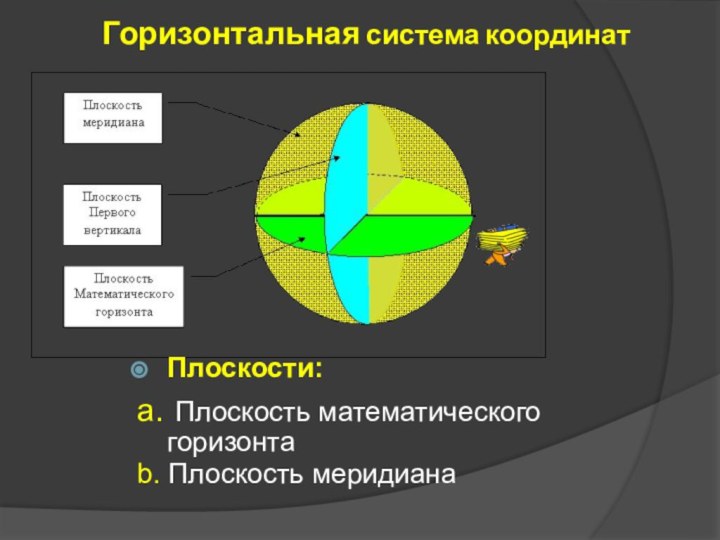
Слайд 44
Горизонтальная система координат
Плоскости:
a. Плоскость математического горизонта
b.
Плоскость меридиана
Слайд 46
Горизонтальная система координат
Плоскости:
Плоскость математического горизонта
Плоскость меридиана
Слайд 47
Точки
Точка отсчета, она же – центр Небесной сферы.
b. Точки Зенита (Z) и Надира (Na), получаемые при
пересечении небесной сферы отвесной линией. Точки Зенита и Надира принадлежат как Кругу Меридиана, так и Кругу Первого вертикала. c. Точки Юга (S) и Севера (N), получаемые при пересечении небесной сферы полуденной линией. Точки Юга и Севера принадлежат как Кругу Меридиана, так и Кругу Математического Горизонта.
d. Точки Востока (Е) и Запада (W), получаемые при пересечении небесной сферы линией ВОСТОК - ЗАПАД. Точки Востока и Запада принадлежат как Кругу Математического горизонта, так и Кругу Первого вертикала.





























