Презентация на тему Движение космических аппаратов

КА С ИДЕАЛЬНО РЕГУЛИРУЕМЫМ ДВИГАТЕЛЕМ МАЛОЙ ТЯГИ
3. ОПТИМИЗАЦИЯ

ТРАЕКТОРИИ ПЕРЕЛЕТА НА ОРБИТУ ВОКРУГ ЛУНЫ КА С ИДЕАЛЬНО РЕГУЛИРУЕМЫМ ДВИГАТЕЛЕМ МАЛОЙ ТЯГИ
4. ОПТИМИЗАЦИЯ МНОГОВИТКОВЫХ ПЕРЕЛЕТОВ МЕЖДУ ЭЛЛИПТИЧЕСКИМИ НЕКОМПЛАНАРНЫМИ ОРБИТАМИ КА С ДВИГАТЕЛЕМ ПОСТОЯННОЙ СКОРОСТИ ИСТЕЧЕНИЯ
ЗАКЛЮЧЕНИЕ

2

численной оптимизации траекторий КА с малой тягой. Основой этого

подхода является формальная редукция краевой задачи принципа максимума к задаче Коши. Такая редукция достигается применением метода продолжения по параметру.

3

Егоров, В.В. Белецкий, Г.Б. Ефимов, М.С. Константинов, Г.Г. Федотов, Ю.А.

Захаров,
Ю.Н. Иванов, В.В. Токарев, В.Н. Лебедев, В.В. Салмин, С.А. Ишков, В.В. Васильев,
T.N. Edelbaum, F.W. Gobetz, J.P. Marec, N.X. Vinh, K.D. Mease, C.G. Sauer, C. Kluever, V. Coverstone-Carroll, S.N. Williams, M. Hechler и др.

Метод продолжения:
M. Kubicek, T.Y. Na и др.

4

вычислительная неустойчивость;
необходимость подбора начального приближения в условиях отсутствия

априорной информации о решении задачи.

Часть этих явлений связана с физической сущностью задачи оптимизации (вопросы устойчивости, существования и ветвления решений). Однако, большинство численных методов вносят свои - методические - ограничения, не имеющие непосредственного отношения к свойствам математической задачи. Так, область сходимости практически всех численных методов существенно меньше области притяжения конкретной экстремальной точки в пространстве неизвестных параметров краевой задачи.

Методические сложности связаны с вычислительной неустойчивостью и с ограниченностью области сходимости численных методов решения, а в некоторых случаях - например при использовании ряда прямых методов оптимизации - с большой размерностью задачи.

5

то есть устранение, по возможности, методических недостатков численной оптимизации. В

частности, была поставлена и решена задача определения оптимальной траектории при использовании тривиального начального приближения (например, пассивного движения КА по начальной орбите).

Рассматриваемые прикладные задач оптимизации траекторий

1. Оптимизация межпланетных траекторий КА с идеально регулируемым двигателем малой тяги;

2. Оптимизация траекторий перелета к Луне КА с идеально регулируемым двигателем малой тяги в рамках ограниченной задачи трех тел;

3. Оптимизация перелетов между некомпланарными эллиптическими орбитами КА с двигательной установкой с постоянной скоростью истечения.

6

ДВИГАТЕЛЕМ МАЛОЙ ТЯГИ
10

СОЛНЕЧНОЙ ЭРДУ
18

ИДЕАЛЬНО РЕГУЛИРУЕМЫМ ДВИГАТЕЛЕМ МАЛОЙ ТЯГИ
Рассматривается задача перелета КА с

идеально регулируемым двигателем малой тяги с геоцентрической орбиты на орбиту спутника Луны. Траектория перелета разбивается на 4 участка:

1) Траектория геоцентрической спиральной раскрутки с начальной орбиты до некоторой промежуточной геоцентрической орбиты;

2) Траектория сопровождения точки либрации L2 системы Земля-Луна;

3) Траектория перелета из точки L2 на некоторую промежуточную селеноцентрическую орбиту;

4) Траектория селеноцентрической скрутки до целевой орбиты.

1-й и 4-й участок могут отсутствовать в случае достаточно высоких начальной геоцентрической и конечной селеноцентрической орбит.

Траектории 2-го и 3-го участков определяются с помощью метода продолжения по параметру.

24

не имеющих особенностей при нулевом наклонении и эксцентриситете. Задача

оптимального управления редуцируется к двухточечной краевой задаче применением принципа максимума Л.С. Понтрягина.

Эта краевая задача, в свою очередь, формально редуцируется к задаче Коши с помощью метода продолжения по параметру. Для вычисления правых частей дифференциальных уравнений метода продолжения необходимо проинтегрировать систему дифференциальных уравнений оптимального движения (П-систему) и вычислить частные производные от конечного фазового вектора П-системы по начальным значениям сопряженных переменных.

При численном интегрировании П-системы ее правые части численно осредняются по истинной долготе КА. Частные производные от конечного фазового вектора П-системы по начальным значениям сопряженных переменных определяются по конечно-разностным соотношениям.

В результате первого интегрирования П-системы формируется вектор невязок решения краевой задачи. Для определения матрицы чувствительности с помощью конечных разностей требуется 6 дополнительных интегрирований П-системы. В результате, после решения системы линейных алгебраических уравнений формируется вектор правых частей системы дифференциальных уравнений метода продолжения.

Система дифференциальных уравнений метода продолжения численно интегрируется по параметру продолжения от 0 до 1, в результате чего определяется оптимальное решения.

32

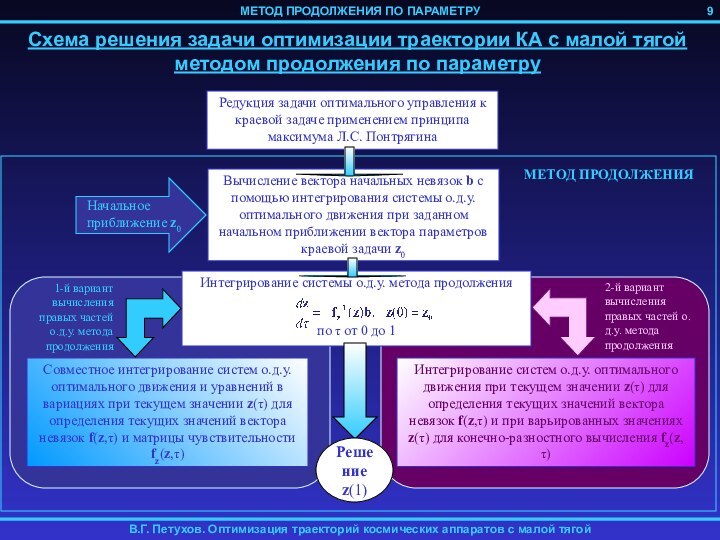
продолжения по параметру.

Для вычисления невязок f интегрируются осредненные по

истинной долготе F уравнения оптимального движения. Эти уравнения имеют особенность при p=0, поэтому использовать нулевое начальное приближение для вектора сопряженных переменных нельзя.

В задаче оптимального быстродействия при использовании метода продолжения по параметру в качестве начального приближения для p(0) выбиралось ph=1, если большая полуось конечной орбиты превышает большую полуось начальной орбиты и ph=-1 в противном случае. Остальные компоненты вектора p выбирались равными 0, а начальное приближение для безразмерного времени перелета T|τ=0=1 (в единицах начальной орбиты). С таким начальным приближением удалось решить задачи об оптимальном по быстродействию перелете с высокоэллиптической промежуточной орбиты (ПО) на ГСО при наклонении ПО 0°-75° и высоте апогея ПО 10000-120000 км. Если высота апогея ПО находилась вне этого диапазона, для решения задачи в качестве начального приближения приходилось использовать предварительно полученное решение задачи перелета с ПО с достаточно близкой высотой апогея.

Осреднение уравнений оптимального движения по истинной долготе F осуществляется численно в процессе интегрирования этих уравнений.

Вычисление частных производных от функции невязок f по параметрам краевой задачи p(0), T, необходимых для применения метода продолжения, производится также численно по конечно-разностным формулам первого порядка.

Таким образом, для вычисления правых частей дифференциальных уравнений метода продолжение используется численное интегрирование численно осредненных уравнений оптимального движения и полученные численным дифференцированием частные производные от функции невязок краевой задачи по ее параметрам.

38

ускорения (по сравнению с гравитационным) обуславливает близость эволюции орбитальных

элементов в осредненном и неосредненном движении в эллиптическом случае.

Для проверки применимости найденного для осредненных уравнений движения оптимального управления, найденные оптимальные начальные значения параметров краевой задачи подставлялись в неосредненные уравнения оптимального движения, и эти уравнения численно интегрировались. Начальное значение истинной долготы F выбиралось достаточно произвольно (обычно соответствующее перигею или апогею начальной орбиты), а начальное значение сопряженной к ней переменной pF принималось равной 0 (см. замечание выше).

В результате этого численного интегрирования определялись фактические невязки на правым конце траектории и программа оптимального управления. Для перелетов на ГСО с высокоэллиптических промежуточных орбит при уровне реактивного ускорения 0.1-0.5 мм/с2 разница в невязках при решении осредненной и неосредненной задач имела величину порядка 0.1%.

Примеры использования оптимального управления, полученного для осредненной задачи к неосредненным уравнениям движения приводятся в следующем разделе.

39

использовать для оптимизации многовитковых перелетов с малой тягой, что

продемонстрировано на примере оптимизации по быстродействию перелетов с эллиптической промежуточной орбиты на ГСО.

2. В настоящее время не обнаружено каких-либо существенных ограничений на возможность использования разработанного метода в задачах с фиксированным временем и с различными краевыми условиями (межорбитальный перелет, набор заданной орбитальной энергии, разворот плоскости орбиты и т.д.).

3. Не обнаружено каких-либо ограничений на возможность учета внешних возмущающих сил при оптимизации траектории КА разработанным методом. Возмущающие силы, выраженные как через орбитальные элементы, так и через фазовый вектор КА, относительно легко могут быть введены в уравнения разработанного метода так как операции осреднения уравнений движения и вычисления производных от невязок краевой задачи по ее параметрам реализованы в рамках этого метода численно. Для учета возмущающих ускорений в уравнениях движения необходимы выражения для частных производных первого порядка от компонент этих ускорений по орбитальным элементам.

4. Разработанный метод позволил провести исчерпывающий анализ оптимальных по быстродействию перелетов с эллиптической промежуточной орбиты на ГСО, включая анализ влияния параметров промежуточной орбиты и основных проектных параметров КА на характеристики перелета и определение номинальных программ управления вектором тяги электроракетной двигательной установки КА.

48