- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Закони Кеплера
Содержание
- 2. Закони Кеплера - три емпіричні залежності, що
- 3. Перший закон КеплераВсі планети обертаються навколо Сонця
- 4. Найближча до Сонця точка орбіти називається перигелієм, а найдальша від нього точка — афелієм.
- 5. Ступінь витягнутості еліпса характеризується його ексцентриситетом. Ексцентриситет
- 6. Другий закон КеплераРадіус-вектор планети (тіла Сонячної системи) за рівні проміжки часу описує рівновеликі площі.
- 7. Лінійна швидкість руху планети неоднакова в різних
- 8. Таким чином, другий закон Кеплера кількісно визначає
- 9. Третій закон КеплераНа відміну від двох перших
- 10. Оа2F2Квадрати зоряних періодів обертання планет відносяться, як куби великих півосей їхніх орбіт.
- 11. Цей закон Кеплера пов'язує середні відстані планет
- 12. Відношення кубу півосі до квадрата періоду обертання
- 13. Третій закон Кеплера відіграє важливу роль в
- 14. Відхилення від законів КеплераЗ погляду фізики, закони
- 15. Скачать презентацию
- 16. Похожие презентации
Закони Кеплера - три емпіричні залежності, що описують рух планет навколо Сонця. Названо на честь німецького астронома Йоганеса Кеплера, який відкрив їх шляхом аналізу спостережень руху Марса навколо Сонця, здійснених данським астрономом Тихо Браге.












Слайд 3
Перший закон Кеплера
Всі планети обертаються навколо Сонця еліптичними
орбітами, в одному з фокусів яких перебуває Сонце (всі
орбіти планет і тіл Сонячної системи мають один спільний фокус, в якому, власне, і розташовано Сонце).Слайд 4 Найближча до Сонця точка орбіти називається перигелієм, а
найдальша від нього точка — афелієм.
Слайд 5 Ступінь витягнутості еліпса характеризується його ексцентриситетом. Ексцентриситет дорівнює
відношенню відстані фокуса від центра до довжини великої півосі
(середньої відстані планети до Сонця). Коли фокуси й центр збігаються, еліпс перетворюється на коло. Орбіти планет — еліпси, які мало відрізняються від кіл; їх ексцентриситети малі. Наприклад, ексцентриситет орбіти Землі е = 0,017.
Слайд 6
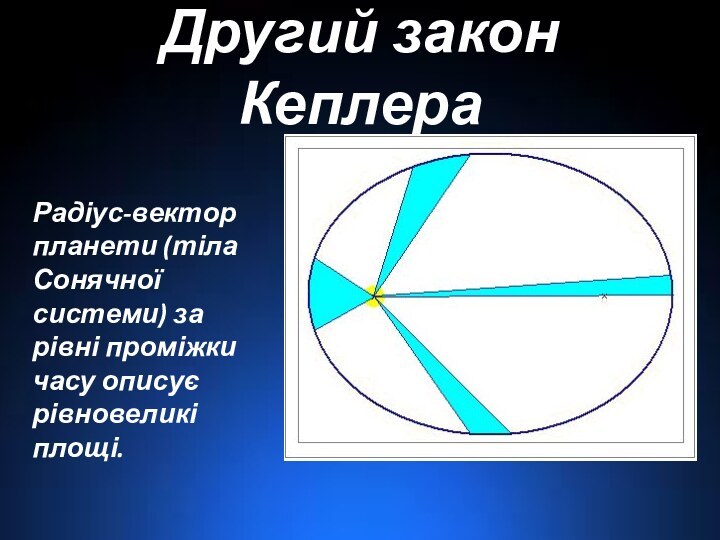
Другий закон Кеплера
Радіус-вектор планети (тіла Сонячної системи) за
рівні проміжки часу описує рівновеликі площі.
Слайд 7 Лінійна швидкість руху планети неоднакова в різних точках
її орбіти: що ближча планета до Сонця, то більша
її швидкість. Швидкість руху планети у перигелії найбільша, а в афелії — найменша. Однак площа, яку "замітає" радіус-вектор за певний проміжок часу, не залежить від того, в якій частині орбіти перебуває планета. Площа, яку "замітає" радіус вектор за одиницю часу називається секторною (сегментною) швидкістю.Слайд 8 Таким чином, другий закон Кеплера кількісно визначає зміну
швидкості руху планети орбітою.
З погляду класичної механіки, другий закон
Кеплера є проявом закону збереження моменту імпульсу.
Слайд 9
Третій закон Кеплера
На відміну від двох перших законів
Кеплера, що стосуються властивостей орбіти кожної окремо взятої планети,
третій закон пов'язує властивості орбіт різних планет між собою. Якщо періоди обертання двох планет та , а довжини великих півосей їхніх орбіт, відповідно, а1 та а2 , то виконується співвідношення:
Слайд 10
О
а
2
F
2
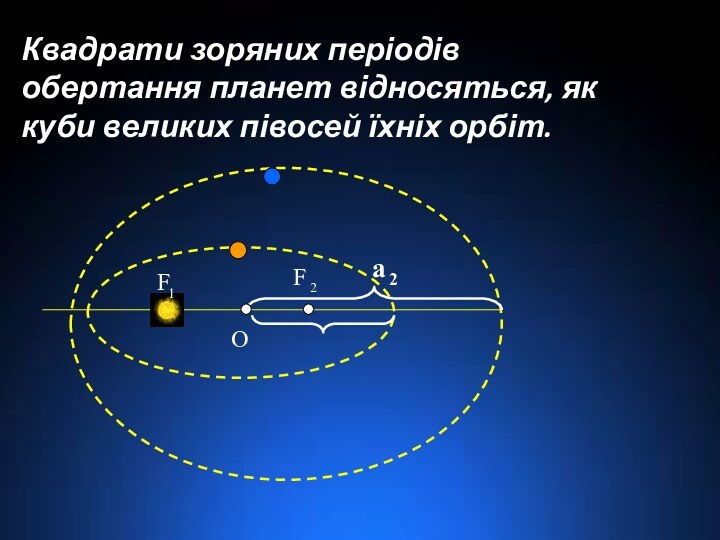
Квадрати зоряних періодів обертання планет відносяться, як куби
великих півосей їхніх орбіт.
Слайд 11 Цей закон Кеплера пов'язує середні відстані планет від
Сонця з їхніми зоряними періодами обертання і надає змогу
встановити відносні відстані планет від Сонця, інакше кажучи, дає змогу подати великі півосі всіх планетних орбіт в одиницях великої півосі земної орбіти.Велику піввісь земної орбіти взято за астрономічну одиницю відстаней, але її абсолютне значення було визначено пізніше, лише у XVIII столітті.
Слайд 12 Відношення кубу півосі до квадрата періоду обертання є
сталою для всіх планет Сонячної системи і залежить лише
від маси Сонця і гравітаційної сталої, як довів пізніше Ньютон:Таким чином, це співвідношення дає можливість «зважити» Сонце.





























