Слайд 2
Взаимодействие между молекулами в реальном газе
Обобщая теорию и
эксперимент можно резюмировать, что силы притяжения между молекулами, также
как и силы отталкивания убывают с расстоянием r между молекулами и очень быстро. Но по разному! Наиболее быстро убывают именно силы отталкивания. Приближенно можно считать, что те и другие обратно пропорциональны некоторой степени r:
Для сил притяжения показатель степени n ≈ 7. Для сил отталкивания показатель m>n и очень существенно зависит от природы взаимодействующих молекул: m может изменяться в диапазоне от 9 до 15.
Слайд 3
Взаимодействие между молекулами в реальном газе
Обычно в теории
реальных газов взаимодействие между молекулами описывают с помощью потенциальной
энергии взаимодействия как функции от расстояния r между центрами
молекул. Расстояние ro на рисунке приблизительно равно диаметру молекулы. Заметим, кстати, что с учетом вероятностного, квантовомеханического движения электронов в молекуле понятие диаметра молекулы определяется не вполне четко.
Слайд 4
Диаметр молекулы
Наиболее удовлетворительные результаты дает следующая аппроксимация кривой
потенциальной энергии:
где а1 и а2 - константы. Первое слагаемое
соответствует силам отталкивания, второе – силам притяжения. Отметим, что для последних шестая степень не противоречит седьмой степени n ≈ 7, потому что потенциал и сила связаны известным соотношением:
Выражение для потенциала называется потенциалом Леннарда-Джонса.
Слайд 5
Диаметр молекулы
Для реальных газов (и жидкостей) часто вводится
модельное понятие сферы молекулярного действия rм.д , логически обоснованное
быстрым уменьшением сил взаимодействия с расстоянием. Считается, что взаимодействуют молекулы только внутри сферы с радиусом rм.д , а вне этой сферы взаимодействие принимается равным нулю. Указать точно величину rм.д невозможно, все зависит от нужной нам точности оценок. Обычно rм.д равен нескольким диаметрам молекул.
Слайд 6
Уравнение Ван-дер-Ваальса
Уравнение состояния для реальных газов можно
получить из соответствующего уравнения для идеальных газов, если правильно
учесть собственный объем молекул и их взаимодействие, то есть то, чем пренебрегают в идеальном газе. Знаки этих двух поправок легко установить с помощью простой логики.
В объеме V молекулы реального газа занимают хотя и небольшой, но конечный объемчик, который несколько уменьшает область свободного движения молекул. Поэтому объемная поправка отрицательна.
Слайд 7
Уравнение Ван-дер-Ваальса
Взаимодействие между молекулами приводит к
дополнительному давлению «самосжатия» реального газа, то есть если вдруг
исчезнет взаимодействие, то потребуется некоторое добавочное внешнее давление, чтобы сохранить газ в прежнем объеме. Таким образом, поправка к давлению положительна.
С конкретным видом поправок дело сложнее, их предлагалось много. Наиболее удачно с точки зрения обобщения многочисленных экспериментальных данных оказалось предложение Ван-дер-Ваальса в 1873 г.
Слайд 8
Уравнение Ван-дер-Ваальса
Для моля газа Vм уравнение
Ван-дер-Ваальса записывается так:
где а и b –
постоянные Ван-дер-Ваальса, определяемые для каждого газа экспериментально.
Поправка b не равна собственному объему молекул. Оценки показывают, что b примерно в четыре раза больше объема молекул.
Слайд 9
Уравнение Ван-дер-Ваальса
Уравнение Ван-дер-Ваальса является кубическим относительно объема, в
чем легко убедиться с помощью элементарных преобразований (для простоты
записи опустим индекс «м» у объема, суть дела от этого не изменится):
В общем случае это уравнение имеет три корня, причем в зависимости от значений коэффициентов либо все три корня вещественны, либо одно вещественное, а два – комплексные. Так как объем может быть только вещественным, то комплексные решения не имеют физического смысла.
Слайд 10
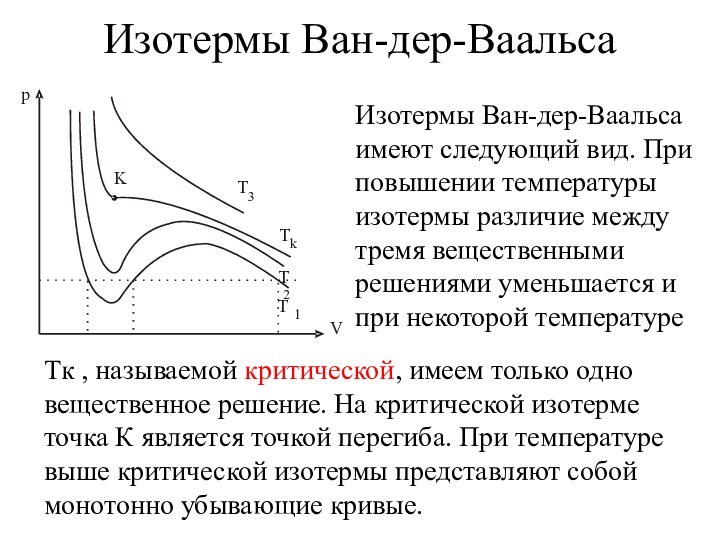
Изотермы Ван-дер-Ваальса
Изотермы Ван-дер-Ваальса имеют следующий вид. При
повышении температуры изотермы различие между тремя вещественными решениями уменьшается
и при некоторой температуре
Tк , называемой критической, имеем только одно вещественное решение. На критической изотерме точка К является точкой перегиба. При температуре выше критической изотермы представляют собой монотонно убывающие кривые.
Слайд 11
Критическая температура
Напомним понятие критической температуры, которое впервые было
введено Менделеевым. На графике зависимости плотности жидкости ρ и
ее насыщенного пара при некоторой температуре
Tк становятся равными и вещество переходит из двухфазного состояния в однородное, однофазное. Жидкость превращается в пар независимо от ее давления и объема. Менделеев называл температуру Tк температурой абсолютного кипения жидкости. Для воды Tк=374оС.
Слайд 12
Сверхкритическое состояние
Экспедиция немецких ученых исследует
в Атлантическом океане глубоководный источник с очень высокой температурой.
Жидкость в нем находятся в необычном, сверхкритическом состоянии.
Зонд опускается в очень горячую воду, почти пар. Это немецкие ученые изучают в южных водах Атлантического океана так называемый «гидротермальный вентиль» с температурой 407 градусов по Цельсию. Пока это самое горячее местечко, обнаруженное на дне океана, хотя всего на пять градусов выше, чем прежний рекорд в 402 градуса, зарегистрированный в Тихом океане. Ученые столкнулись с интересным случаем, когда морская вода в источнике находится в сверхкритическом состоянии.
Слайд 13
«Черный курильщик»
Гидротермальный вентиль, известный также под названием «черный
курильщик», ученые нашли на юге от экватора на глубине
2990 метров. При высокой температуре и давлении выше 298 бар вода в нем переходит в сверхкритическое состояние типа плотного пара.
В этом состоянии она может проникать через твердые тела как газ и растворять материалы подобно жидкости.
Слайд 14
«Черный курильщик»
В промышленности, например, сверхкритическую углекислоту
и воду используют в качестве растворителя именно из-за таких
необычных свойств. На дне океана сверхкритическая морская вода может растворять и перемещать минералы из камней по- другому, чем в других горячих вентилях. Исследователи собрали образцы чистой сверхкритической жидкости, полный химический анализ которой проведут в лабораторных условиях.
Может быть, нам удастся узнать нечто новое о том, как могут переносить такие необычные условия живые организмы?
Слайд 15
Силы адгезии
Индийских ученых лягушка вдохновила
на создание клейкой ленты, которая прилипает в тридцать раз
сильнее, чем современные аналоги. Адгезия (от латинского «прилипание») – это сцепление поверхностей различных твердых или жидких тел. На ее силу влияют межмолекулярные взаимодействия (силы Ван-дер-Ваальса) в поверхностном слое материалов.
Адгезия оказывает значительное влияние на природу трения контактирующих тел: чем ниже адгезия, тем меньше трение.
Слайд 16
Силы адгезии
Когда обычную клейкую ленту отрывают
от поверхности, клеящий слой разрушается, а пыль и другие
прилипшие частицы ухудшают ее способность к прилипанию. Строение подушечек пальцев древесной лягушки и сверчка вдохновили индийских исследователей на создание клейкой ленты, которая была бы, с одной стороны, прочной, с другой стороны, ее можно было бы использовать много раз. Ведь обычную ленту можно использовать один или два раза, а ящерицы и жабы используют свои конечности постоянно.
Прилипающие подушечки пальцев у древесной лягушки устроены особым образом.
Слайд 17
Силы адгезии
Под прилипающими подушечками пальцев древесной лягушки прячутся
сосудики с жидкостью, железы и кровеносные сосуды. Следуя примеру
природы,
ученые изготовили клейкую ленту, которая представляет собой эластичный материал с микроканалами, заполненными воздухом или маслом. Такая конструкция, обнаружили авторы, делает материал намного более «прилипчивым».
Слайд 18
Силы адгезии
«Из-за капиллярного давления силы адгезии увеличиваются в
тридцать раз», - объясняют японские ученые. Кроме того, они
показали, что на адгезивные свойства влияет толщина самого слоя, диаметр канальцев и другие параметры.
Ученые планируют использовать новую технологию для многократно используемых адгезивных устройств и для наклеивания стикеров. «Одно из применений – для стикеров на посуде, фруктах, когда вы хотите удалить их без остатка, чтобы не оставался клеящий слой», - говорят ученые.
Слайд 19
Абсолютный нуль и ниже
Рассмотрим понятие температуры
несколько глубже и шире, чем это принято в кратких
курсах общей физики. Подойдем к вопросу с позиций, так скажем, Большой физики.
Обычно температуру связывают со средней кинетической энергией частиц. Которая, естественно, не может быть отрицательной. Поэтому и говорят, что отрицательных абсолютных (то есть по шкале Кельвина) температур не может быть никогда.
Но такое понятие температуры вводится лишь для термодинамически равновесных состояний.
Физика не ограничивается изучением только термодинамически равновесных состояний.
Слайд 20
Абсолютный нуль и ниже
Запишем распределение Больцмана в виде:
Доля n/n0 частиц с данной энергией U в
силовом поле любой природы зависит только от температуры. Это и позволяет придать температуре более универсальную трактовку – как меры, от которой зависит распределение частиц по энергиям. Чем ниже температура, тем быстрее убывает доля n/n0 с возрастанием энергии U.
При таком подходе ничто не мешает некоторым физическим системам иметь и отрицательные температуры: если n0, но если n>n0 , то T<0.
Слайд 21
Абсолютный нуль и ниже
В классических системах
отрицательные температуры не реализуются. Но с 1926 г. известен
такой раздел физики, как квантовая механика, которая изучает, разумеется, квантовые системы.
В квантовой системе распределение частиц по разрешенным квантовыми законами энергетическим уровням определяется формулой Больцмана. При положительных температурах на нижних уровнях будет больше частиц, чем на верхних. Если температуру увеличивать, подводя энергию, то количество частиц на верхних уровнях будет возрастать и при стремлении температуры к бесконечности распределение стремится к равномерному по всем уровням: n=n0 , при T= ∞.
Слайд 22
Абсолютный нуль и ниже
В простейшем случае
двухуровневой системы если подводить энергию к системе уже достигшей
равнораспределения, то получим состояние с n>n0 , то есть отрицательные абсолютные температуры! Только по сравнению с обычными классическими системами пришлось не охлаждать систему, отводя энергию, а нагревать. Говорят, что при n>n0 имеем состояние с инверсной населенностью уровней.
Состояния с отрицательными абсолютными температурами крайне неравновесны, для их поддержания необходим непрерывный подвод энергии. Если прекратить этот подвод, система быстро перейдет в состояние с нормальным больцмановским распределением (при T>0).
Слайд 23
Ожижение газов
Для того чтобы ожижить газ, необходимо
охладить его ниже критической температуры Тк . Перевод таких
газов, как кислород, азот, водород и гелий, в жидкое состояние требует сильного понижения их температуры. Один из промышленных методов ожижения газов (метод Ливде) использует для охлаждения газа эффект Джоуля — Томсона.
Эффект Джоуля-Томсона заключается в следующем: пропуская газ по теплоизолированной трубке с пористой перегородкой, Джоуль и Томсон обнаружили, что при расширении, которым сопровождается прохождение газа через перегородку, температура его несколько изменяется.
Слайд 24
Эффект Джоуля-Томсона
В зависимости от начальных давления и температуры
изменение температуры ΔT имеет тот или иной знак и,
в частности, может оказаться равным нулю. Это явление получило название эффекта Джоуля — Томсона. Если температура газа понижается (ΔT <0), эффект считается положительным; если газ нагревается (ΔT ,>0), эффект считается отрицательным.
Эффект Джоуля — Томсона всецело обусловлен отклонениями газа от идеальности.
Слайд 25
Метода Линде
Сжатый компрессором К газ проходит через холодильник
X, в котором охлаждается до температуры, лежащей ниже точки
инверсии. Это нужно для
того, чтобы при последующем расширении газ в результате эффекта Джоуля — Томсона не нагревался, а охлаждался. Затем газ течет по внутренней трубке теплообменника Т.О. и, пройдя через дроссель Д сильно расширяется и охлаждается.