- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по физики на тему: Волны
Содержание
- 2. Продольные и поперечные волны
- 3. Продольные и поперечные волны. Волны на поверхности
- 4. Продольные и поперечные волны. Волны на поверхности
- 5. Продольные и поперечные волны. Волны на поверхности
- 6. Продольные и поперечные волны. Волны на поверхности
- 7. Продольные и поперечные волны. Волны на поверхности
- 8. Интерференция волн
- 9. Интерференция волн на поверхности жидкости.Круговая волна на
- 10. Интерференция волн на поверхности жидкости.Интерференция между двумя
- 11. Интерференция волн на поверхности жидкости.Интерференция круговой волны
- 12. Интерференция волн на поверхности жидкости.Интерференция круговой волны
- 13. Интерференция волн на поверхности жидкости.Дифракция круговой волны
- 14. Интерференция волн на поверхности жидкости.Стоячая волна, образующаяся
- 15. Отражение ударных волн
- 16. Отражение ударных волн.Ударная волна образуется в точечном
- 17. Отражение ударных волн.Ударная волна образуется в точечном
- 18. Возможные типы колебаний атомов в кристалле.
- 19. Генерация акустической волны громкоговорителем.
- 20. Эффект Доплера
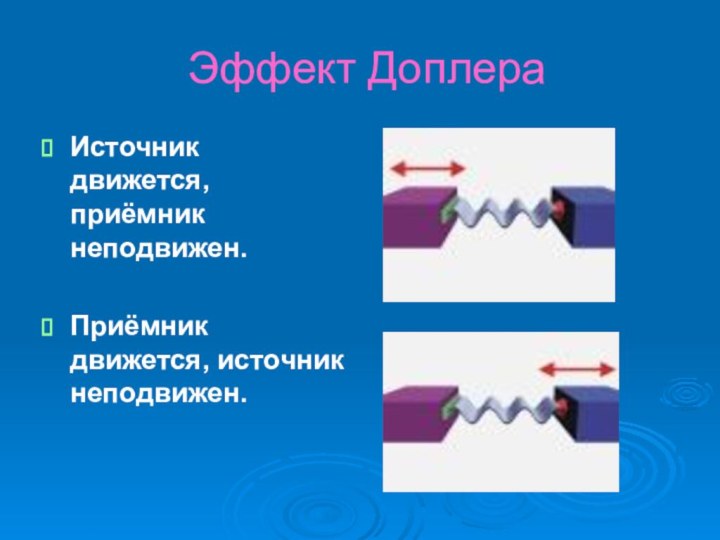
- 21. Эффект ДоплераЭффект Доплера в акустике. Частота регистрируемого
- 22. Эффект ДоплераИсточник движется, приёмник неподвижен. Приёмник движется, источник неподвижен.
- 23. Разложение сигнала в ряд Фурье.Анимация показывает сумму
- 24. Разложение сигнала в ряд Фурье.Анимация показывает сумму
- 25. Ударные волныУдарные волны. Источник звука движется со звуковой скоростью. Впереди источника формируется ударная волна.
- 26. Ударные волныИсточник движется с дозвуковой скоростью. Наблюдается эффект Доплера
- 27. Скачать презентацию
- 28. Похожие презентации
Продольные и поперечные волны


























Слайд 4
Продольные и поперечные волны. Волны на поверхности жидкости
Поперечная
волна в сетке, состоящей из шариков, скреплённых пружинками. Колебания
масс происходят перпендикулярно направлению распространения волны.