- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Дифракция света
Содержание
- 2. Дифракцией света называется явление отклонения света от
- 3. Если на пути параллельного
- 4. Если препятствие имеет линейный
- 5. Условия наблюдения Для наблюдения дифракции света
- 6. Дифракцию света наблюдал в 1802 г.
- 7. Принцип Гюйгенса-ФренеляВолновая поверхность в любой момент времени
- 8. Для того, чтобы дифракционная картина была достаточно
- 9. Дифракционная решетка Этот оптический прибор представляет
- 10. Дифракционная решеткаПластинка с большим числом чередующихся прозрачных и непрозрачных полос
- 11. Дифракционная решетка увеличена
- 12. Решетки представляют собой периодические
- 13. Простейшая дифракционная решетка состоит из прозрачных участков
- 14. При прохождении через дифракционную решетку пучок белого
- 15. На рис. изображены спектры различных порядков для
- 16. Формула дифракционной решеткиdsinφ=kλ,где k=0,1,2,3,... называется порядком главного максимума
- 17. ПрименениеИсследование спектрального состава веществаИзмерение длины волны
- 18. Дифракционные решетки применялись для спектрального анализа уже
- 19. Он наносил до 300 линий на 1
- 20. Дифракция в природеЕсли рассмотреть под микроскопом крылья
- 21. Что такое голография?Среди разнообразных практических применений волновых
- 22. Скачать презентацию
- 23. Похожие презентации
Дифракцией света называется явление отклонения света от прямолинейного направления распространения при прохождении вблизи препятствий. Как показывает опыт, свет при определенных условиях может заходить в область геометрической тени.




















Слайд 3 Если на пути параллельного светового
пучка расположено круглое препятствие (круглый диск, шарик или круглое
отверстие в непрозрачном экране), то на экране, расположенном на достаточно большом расстоянии от препятствия, появляется дифракционная картина – система чередующихся светлых и темных колец.Слайд 4 Если препятствие имеет линейный характер
(щель, нить, край экрана), то на экране возникает система
параллельных дифракционных полос.
Слайд 5
Условия наблюдения
Для наблюдения дифракции света необходимо
создать определенные условия: длина волны должна быть сравнима с
размерами препятствий.На расстоянии L от препятствия дифракция наблюдается, если
L≈D²/4λ, D – линейные размеры препятствия, λ – длина волны.
Слайд 6 Дифракцию света наблюдал в 1802 г. англ.физик
Томас Юнг, открывший интерференцию.
Исследование дифракции световых волн получило свое
завершение в работах фран.физика Огюстена Жана Френеля (1788-1827) в 1816-1827г.г. В своем труде «Мемуар о дифракции света», опубликованном в 1819 году, Френель продемонстрировал, что итоговая волна не просто огибающая, а результат интерференции вторичных волн. Это уточненная формулировка называется сейчас принципом Гюйгенса-Френеля.
Слайд 7
Принцип Гюйгенса-Френеля
Волновая поверхность в любой момент времени представляет
собой не просто огибающую вторичных волн, а результат их
интерференции.Слайд 8 Для того, чтобы дифракционная картина была достаточно яркой,
нужно пропускать свет через несколько параллельных щелей.
Оптический прибор,
представляющий собой совокупность большого числа препятствий и отверстий, сосредоточенных в ограниченном пространстве, на которых происходит дифракция света, называется дифракционной решеткой.
Слайд 9
Дифракционная решетка
Этот оптический прибор представляет собой
отражающую или прозрачную пластинку с нанесенными на нее параллельными
штрихами. В 1786 году американский астроном Дэвид Риттенхаус (1732-1796) обнаружил, что, пропуская через такую решетку белый свет, можно получить его спектр. Причем, в отличие от призмы, решетка дает не один, а несколько спектров.
Слайд 10
Дифракционная решетка
Пластинка с большим числом чередующихся прозрачных и
непрозрачных полос
Слайд 11
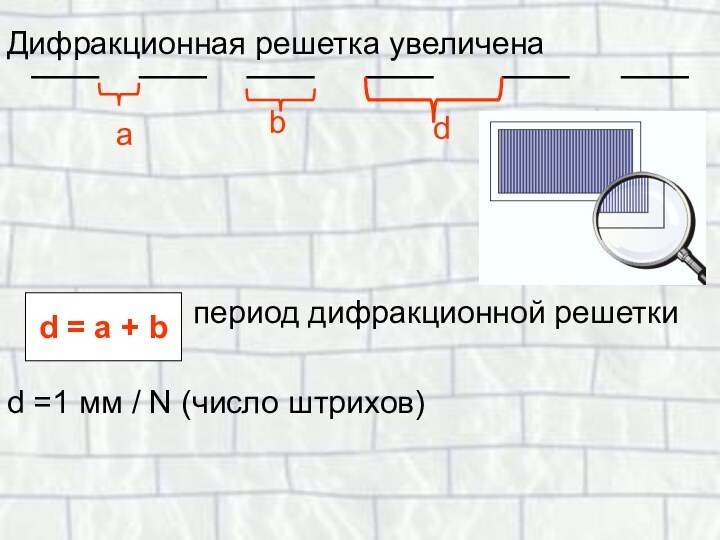
Дифракционная решетка увеличена
период дифракционной решетки
d =1
мм / N (число штрихов)а
b
d
d = a + b
Слайд 12 Решетки представляют собой периодические структуры,
выгравированные специальной делительной машиной на поверхности стеклянной или металлической
пластинки. У хороших решеток параллельные друг другу штрихи имеют длину порядка 10 см, а на каждый миллиметр приходится до 2000 штрихов. При этом общая длина решетки достигает 10–15 см. Изготовление таких решеток требует применения самых высоких технологий. На практике применяются также и более грубые решетки с 50 – 100 штрихами на миллиметр, нанесенными на поверхность прозрачной пленки. В качестве дифракционной решетки может быть использован кусочек компакт-диска или даже осколок граммофонной пластинки. Ваши ресницы также могут играть роль дифракционной решетки.Слайд 13 Простейшая дифракционная решетка состоит из прозрачных участков (щелей),
разделенных непрозрачными промежутками. Если на решетку падает свет, то
в каждом порядке дифракции возникает спектр исследуемого излучения, причем фиолетовая часть спектра располагается ближе к максимуму нулевого порядка.Слайд 14 При прохождении через дифракционную решетку пучок белого света
разлагается в спектр. Наибольшее значение угол дифракции имеет для
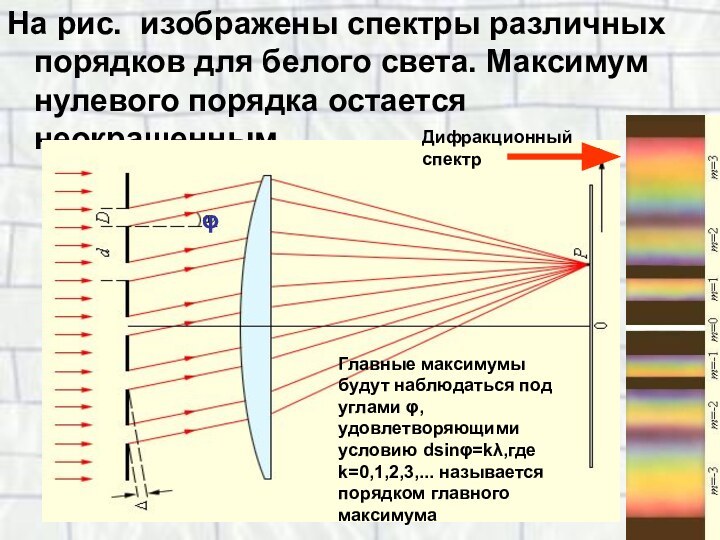
красного света. Наименьшее значение – для фиолетового.Слайд 15 На рис. изображены спектры различных порядков для белого
света. Максимум нулевого порядка остается неокрашенным.
φ
Главные максимумы будут наблюдаться
под углами φ, удовлетворяющими условию dsinφ=kλ,где k=0,1,2,3,... называется порядком главного максимумаДифракционный спектр
Слайд 16
Формула дифракционной решетки
dsinφ=kλ,
где k=0,1,2,3,... называется порядком главного максимума
Слайд 18 Дифракционные решетки применялись для спектрального анализа уже в
начале XIX века.
Первым с этой целью их использовал
немецкий оптик Йозеф Фраунгофер (1787-1826).
Слайд 19 Он наносил до 300 линий на 1 мм
поверхности пластины.
А сейчас самые, пожалуй, распространенные решетки –
лазерные диски. Области, на которых зафиксирована информация, имеют микроскопические бугорки, а запись производится по концентрическим окружностям. В результате поверхность компакт-диска образует одну большую решетку. В современных дифракционных решетках до 2400 линий на 1 мм. Изготовлять их механически невозможно, поэтому используется другой метод: фотографируют картину интерференции двух световых пучков, пересекающихся под углом. Она имеет вид параллельных полос, расстояние между которыми порядка длины волны падающего света.
Слайд 20
Дифракция в природе
Если рассмотреть под микроскопом крылья бабочек,
то можно заметить, что они состоят из большого числа
элементов, размер которых имеет порядок длины видимого света. Таким образом, крыло бабочки представляет собой своеобразную дифракционную решетку. Радужная полоска видна в глазах стрекоз и других насекомых. Она образуется благодаря тому, что их сложные глаза состоят из большого числа отдельных «глазков» -фасеток, т.е тоже являются «живыми» дифракционными решетками.
Слайд 21
Что такое голография?
Среди разнообразных практических применений волновых свойств
света одно из наиболее интересных – голография.
Идеи и принципы
голографии сформулировал в 1948 г. венгерский физик Деннис Габор. Голографический метод получения изображения состоит из двух этапов. Сначала получают голограмму – интерференционную картину, возникающую на фотопластинке при сложении двух когерентных пучков света. Один из них отражается от зеркала, другой от предмета. Эти пучки света образуют на фотопластинке интерференционную картину, представляющую собой чередование светлых и темных пятен. Процесс получения изображения с помощью голограммы называют восстановлением. Для восстановления голограммы на неё направляют опорный пучок когерентного света. Опорный пучок, падая на голограмму, возбуждает в прозрачных ее местах колебание вторичных источников. По принципу Гюйгенса-Френеля вторичные источники создают в окружающем пространстве такую же картину волновых полей, какая была в сигнальном пучке от предмета. Точное совпадение восстановленного волнового фронта с сигнальным приводит к тому, что воспринимаемое зрением изображение по внешнему виду неотличимо от предмета.