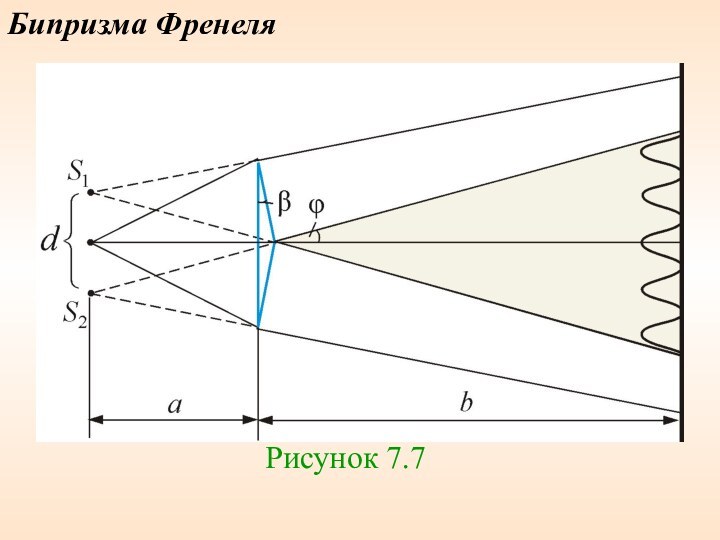
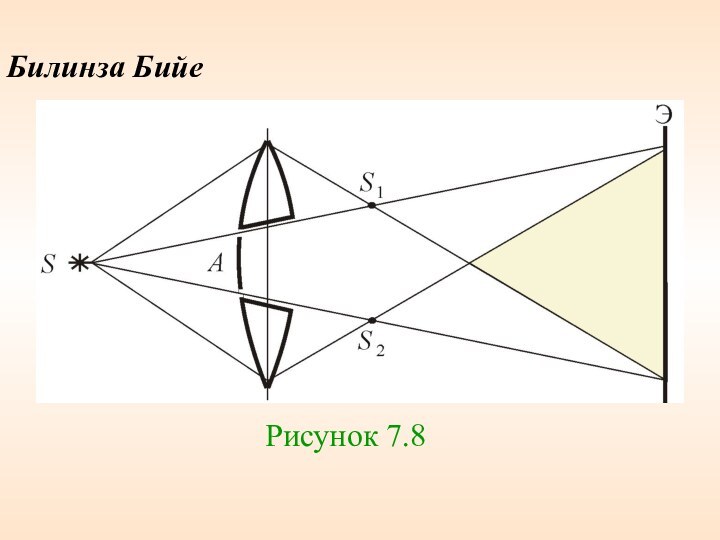
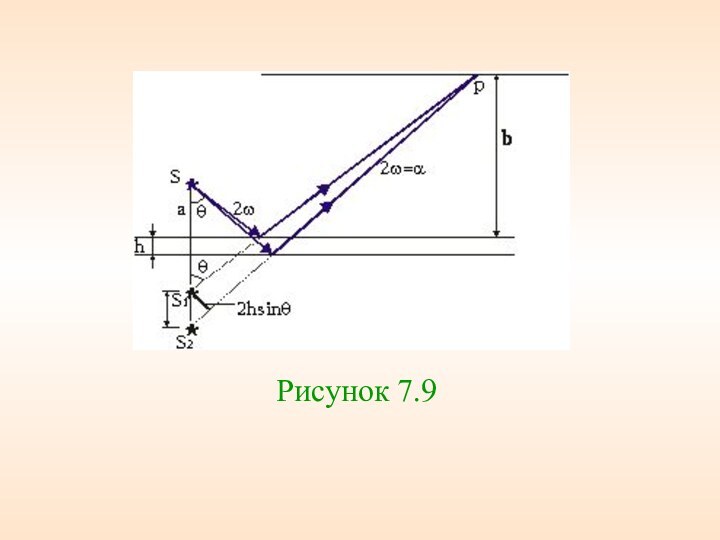
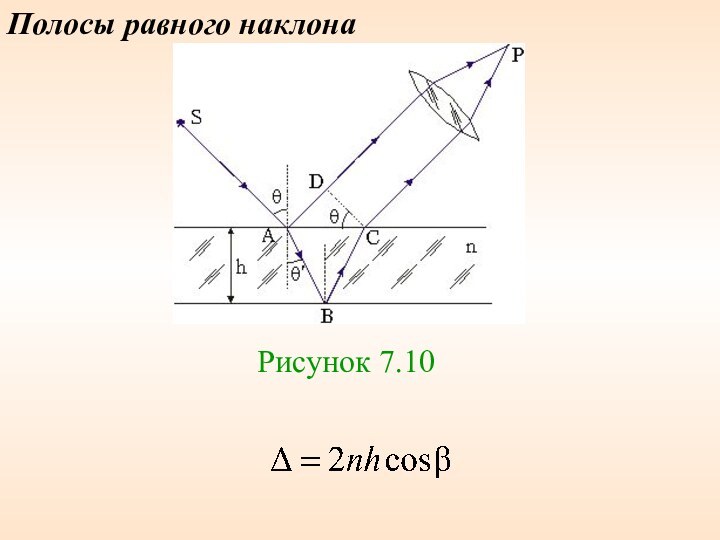
физик, член Эдинбургского королевского общества (с 1855 года) и
Лондонского королевского общества (13.VI.1831 - 5.XI.1879) - английский физик, член Эдинбургского королевского общества (с 1855 года) и Лондонского королевского общества (с 1861 года). Под руководством Максвелла создана известная Кавендишская
лабораториялаборатория в Кембридже, которую и возглавлял до конца жизни. Научные труды посвящены электродинамикелаборатория в Кембридже, которую и возглавлял до конца жизни. Научные труды посвящены электродинамике, молекулярной физикелаборатория в Кембридже, которую и возглавлял до конца жизни. Научные труды посвящены электродинамике, молекулярной физике, общей статистикелаборатория в Кембридже, которую и возглавлял до конца жизни. Научные труды посвящены электродинамике, молекулярной физике, общей статистике, оптикелаборатория в Кембридже, которую и возглавлял до конца жизни. Научные труды посвящены электродинамике, молекулярной физике, общей статистике, оптике, механикелаборатория в Кембридже, которую и возглавлял до конца жизни. Научные труды посвящены электродинамике, молекулярной физике, общей статистике, оптике, механике, теории упругостилаборатория в Кембридже, которую и возглавлял до конца жизни. Научные труды посвящены электродинамике, молекулярной физике, общей статистике, оптике, механике, теории упругости. Самым большим достижением Максвелла является созданная им в 1860-1865 годах теория электромагнитного полялаборатория в Кембридже, которую и возглавлял до конца жизни. Научные труды посвящены электродинамике, молекулярной физике, общей статистике, оптике, механике, теории упругости. Самым большим достижением Максвелла является созданная им в 1860-1865 годах теория электромагнитного поля, которую он сформулировал в виде системы нескольких уравнений, выражающих все основные закономерности электромагнитных явлений.