- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Вопросы по статике
Содержание
- 2. Отчего присохшую пробку с резьбой легче отвернуть,
- 3. Длинный стержень легче удерживать в горизонтальном положении
- 4. Что труднее переломить — целую спичку или
- 5. Почему мяч не остается в покое на
- 6. Почему конькобежцы, разгоняясь, размахивают руками? Резкие
- 7. Лестница, центр тяжести которой находится посередине, опирается
- 8. В какую сторону будут двигаться катушки с
- 9. Мальчик подтягивается вверх, используя неподвижный блок. Выигрывает
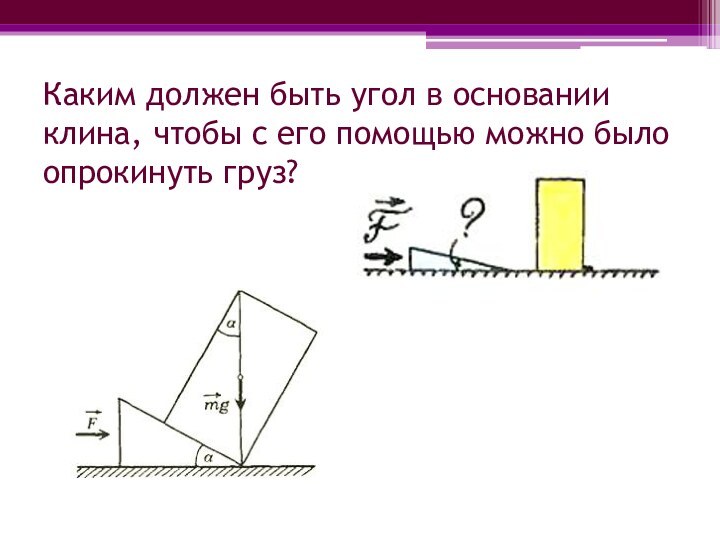
- 10. Каким должен быть угол в основании клина, чтобы с его помощью можно было опрокинуть груз?
- 11. Бруски пытаются сдвинуть с места рычагом. Какой
- 12. На невесомом рычаге уравновешены стальные шары. Нарушится ли равновесие, если шары погрузить в воду? Не нарушится?
- 13. Два мальчика стоят на противоположных сторонах канавы
- 14. По наклонной плоскости при помощи веревки поднимают
- 15. Почему доска обычно плавает в воде широкой
- 16. Для чего к воздушному змею приделывают хвост?
- 17. Почему значительно легче удерживать на пальце швабру,
- 18. Поставьте неваляшку (Ваньку-встаньку) на шероховатую доску и
- 19. Как объяснить сохранение равновесия в данных случаях?Центр
- 20. Однородный стержень согнули посередине под прямым углом.
- 21. Найдите центр тяжести системы шаров, находящихся в
- 22. Можно ли найти центр тяжести «гантели», состоящей
- 23. Почему трудно передвигаться на ходулях?Центр тяжести человека
- 24. Когда канатоходцу легче удержать равновесие — при
- 25. Занимательные опыты по статике
- 26. Сложи две вилки так, чтобы зубья одной
- 27. Положи одну спичку на стол, а на
- 28. Если стол совершенно горизонтален и прочно стоит
- 29. Скачать презентацию
- 30. Похожие презентации






















Слайд 2 Отчего присохшую пробку с резьбой легче отвернуть, если
плотно обмотать ее несколькими слоями ткани?
захвата, во-вторых, слой материи, намотанной на пробку, увеличивает плечо сил, отвертывающих пробку, в то время как момент сил сцепления пробки со стенками сосуда не изменяется.Слайд 3 Длинный стержень легче удерживать в горизонтальном положении за
середину, чем за конец. Почему?
Если стержень удерживать за
середину, необходимо приложить силу, равную силе тяжести стержня. Если же удерживать его за конец, надо создать момент, уравновешивающий, момент силы тяжести стержня. Так как плечо удерживающей силы меньше половины длины стержня, то эта сила будет больше силы тяжести. Слайд 4 Что труднее переломить — целую спичку или ее
половинку?
Половинку. Меньше плечо, больше сила.
А можно так: чем
меньше длина, тем жесткость больше?Слайд 5 Почему мяч не остается в покое на наклонной
плоскости?
Если угол α наклонной плоскости к горизонту таков,
что tg α < k, где k — коэффициент трения между плоскостью и мячом, то точка соприкосновения мяча с плоскостью не скользит по ней. Сила тяжести мяча создает момент, который заставляет мяч поворачиваться вокруг этой точки. При tg α > k мяч катится по наклонной плоскости с проскальзыванием. По абсолютно гладкой поверхности мяч скользил бы не вращаясь.
Слайд 6
Почему конькобежцы, разгоняясь, размахивают руками?
Резкие движения ног
конькобежца вызывают появление моментов сил, стремящихся повернуть его корпус
вокруг вертикальной оси. Поэтому конькобежец в такт движению ног размахивает руками так, чтобы движением рук создать компенсирующие моменты сил.Слайд 7 Лестница, центр тяжести которой находится посередине, опирается на
абсолютно гладкие пол и стену. Какой должна быть сила
натяжения веревки, привязанной к середине лестницы, чтобы удержать ее от падения?Моменты сил реакции пола и стены, а также момент силы натяжения веревки относительно точки О равны нулю при любой силе натяжения. Момент силы тяжести относительно той же точки отличен от нуля. Лестница упадет.
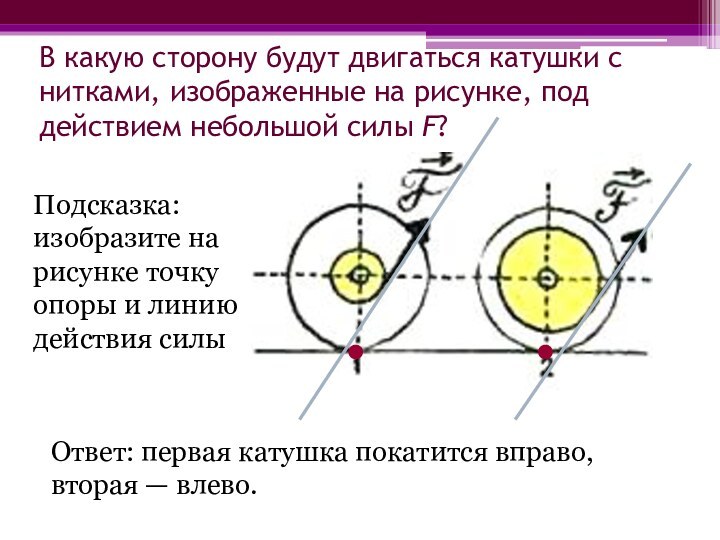
Слайд 8 В какую сторону будут двигаться катушки с нитками,
изображенные на рисунке, под действием небольшой силы F?
Ответ:
первая катушка покатится вправо, вторая — влево.Подсказка: изобразите на рисунке точку опоры и линию действия силы
Слайд 9 Мальчик подтягивается вверх, используя неподвижный блок. Выигрывает ли
он при этом в силе?
Да, примерно в два
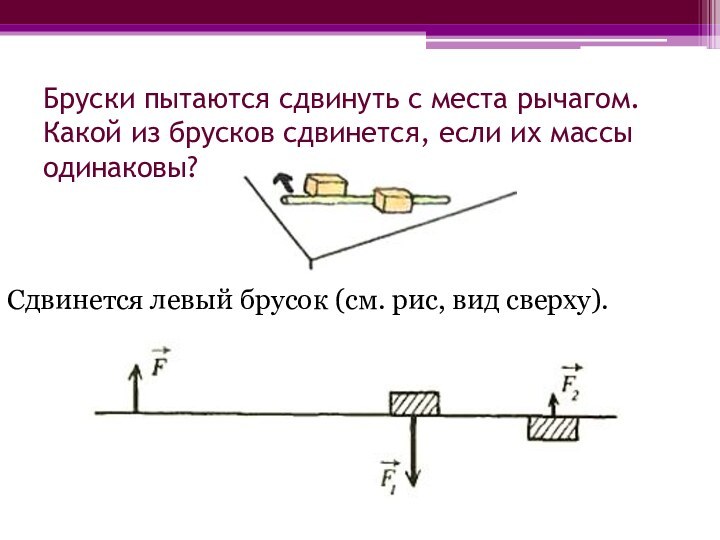
раза? Слайд 11 Бруски пытаются сдвинуть с места рычагом. Какой из
брусков сдвинется, если их массы одинаковы?
Сдвинется левый брусок
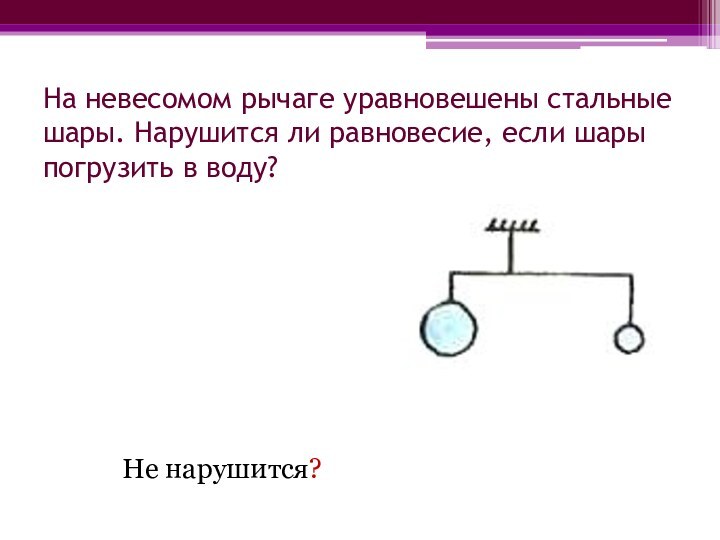
(см. рис, вид сверху). Слайд 12 На невесомом рычаге уравновешены стальные шары. Нарушится ли
равновесие, если шары погрузить в воду?
Не нарушится?
Слайд 13 Два мальчика стоят на противоположных сторонах канавы с
водой. У каждого из них — доска, длина которой
немного меньше ширины канавы. Как им с помощью досок перебраться через канаву?Слайд 14 По наклонной плоскости при помощи веревки поднимают бочку.
Какой выигрыш в силе получают при таком подъеме?
Применение веревки,
перекинутой через бочку, дает выигрыш в силе в два раза (подвижный блок), наклонная плоскость (при α = 30°) — также в два раза; следовательно, общий выигрыш в силе — в четыре раза. Слайд 15 Почему доска обычно плавает в воде широкой гранью
горизонтально, а не вертикально, хотя оба положения доски равновесные?
При
малейшем отклонении доски от вертикали момент выталкивающей силы относительно центра тяжести доски увеличивает отклонение доски, и она опрокидывается в устойчивое горизонтальное положение. Я бы сравнила положение центра тяжести в этих двух ситуациях. Можно составить отдельную задачу.
Слайд 16
Для чего к воздушному змею приделывают хвост?
Хвост
обеспечивает устойчивость змея относительно вращений около вертикальной оси, проходящей
через его центр тяжести.Слайд 17 Почему значительно легче удерживать на пальце швабру, перевернутую
«вверх ногами», чем палку той же длины?
Для удержания щвабры
или палки нужно при их отклонении успевать двигать пальцем так, чтобы они вновь оказывались в положении равновесия, так как равновесие неустойчивое. Щвабра будет отклоняться медленнее, чем палка той же длины, так как центр тяжести щвабры лежит выше центра тяжести палки. Я бы вспомнила инертные свойства.
Слайд 18 Поставьте неваляшку (Ваньку-встаньку) на шероховатую доску и слегка
приподнимите один из концов доски. Как Вы думаете, в
какую сторону отклонится голова игрушки при сохранении её равновесия?Центр тяжести С неваляшки находится ниже геометрического центра О шарообразной поверхности «туловища». В положении равновесия точка С и точка касания А игрушки с наклонной плоскостью должны находиться на одной вертикали; следовательно «голова» неваляшки отклонится влево.
Слайд 19
Как объяснить сохранение равновесия в данных случаях?
Центр тяжести
системы карандаш – нож (линейка – молоток) лежит ниже
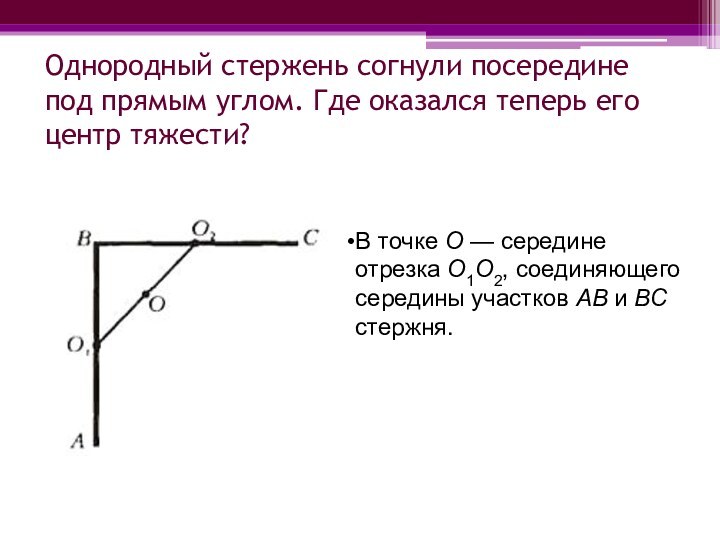
точки опоры.Слайд 20 Однородный стержень согнули посередине под прямым углом. Где
оказался теперь его центр тяжести?
В точке O — середине
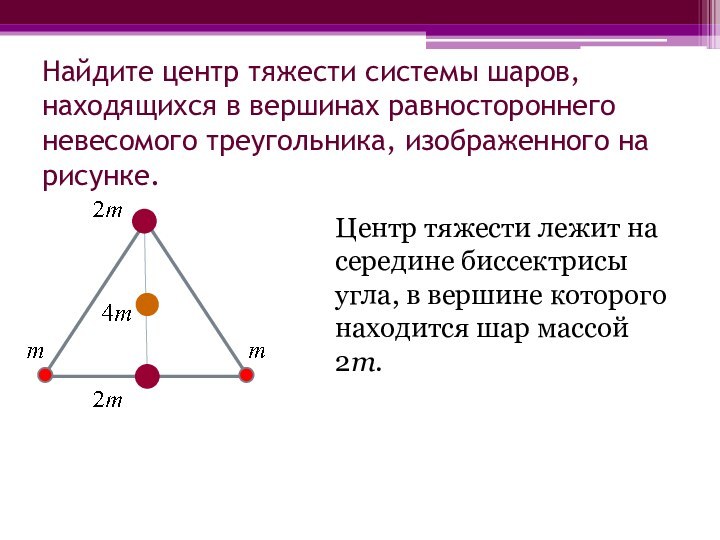
отрезка O1O2, соединяющего середины участков АВ и ВС стержня. Слайд 21 Найдите центр тяжести системы шаров, находящихся в вершинах
равностороннего невесомого треугольника, изображенного на рисунке.
Центр тяжести лежит на
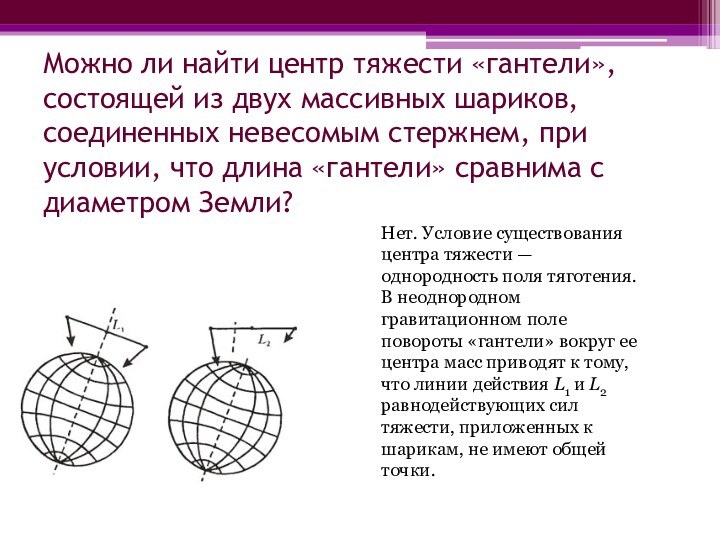
середине биссектрисы угла, в вершине которого находится шар массой 2m.Слайд 22 Можно ли найти центр тяжести «гантели», состоящей из
двух массивных шариков, соединенных невесомым стержнем, при условии, что
длина «гантели» сравнима с диаметром Земли?Нет. Условие существования центра тяжести — однородность поля тяготения. В неоднородном гравитационном поле повороты «гантели» вокруг ее центра масс приводят к тому, что линии действия L1 и L2 равнодействующих сил тяжести, приложенных к шарикам, не имеют общей точки.
Слайд 23
Почему трудно передвигаться на ходулях?
Центр тяжести человека на
ходулях значительно повышается, а площадь его опоры на землю
уменьшается. Значит устойчивость уменьшается.Слайд 24 Когда канатоходцу легче удержать равновесие — при обычном
передвижении по канату или при переносе сильно изогнутого коромысла,
нагруженного ведрами с водой?Во втором случае, так как центр масс канатоходца с ведрами лежит ниже, т.е. ближе к опоре — канату.





























