Слайд 2
Содержание
1) философия зеркал
2) математика зазеркалья
3) физика зеркал
- плоские
зеркала
- отражение в плоском зеркале
- законы отражения
-расположение под углом
друг к другу
- применение плоских зеркал
- сферические зеркала
- вогнутые зеркала
- выпуклые зеркала
- фокусное расстояние
- построение изображения в вогнутом зеркале
- формула сферического зеркала
- линейное увеличение
- применение сферических зеркал
- процесс отражения
4) волшебные зеркала
- способы производства волшебных зеркал
5) решение задач
6) задачи
7) список литературы
Слайд 3
Всю свою историю человек пытается познать мир. Но
познание мира - это, в первую очередь, познание себя.
Зеркало можно назвать техническим инструментом нашей самоидентификации, которая является основой в нашем познании мира. Наше самосознание, представление о себе и мире формируются с помощью и под влиянием зеркала. Иногда мы принимаем зазеркалье как отдельный мир, живущий по своим законам, населенный нашими двойниками и дубликатами окружающих нас вещей. Так что же, собственно говоря, происходит в зазеркалье? По каким законам оно живет?
философия зеркал
Слайд 4
Название это очень условно. И выбрано в честь

Льюиса Кэрролла, который был математиком и описал законы зазеркалья.
В зеркале все предметы "переворачиваются", предстают обращенными. Если вы протянете своему отражению правую руку, то увидите, что оно протягивает вам левую. Законы движения в зазеркалье так же вывернуты, как и неподвижные отражения. В самом деле, в ответ на помахивание правой рукой отражение машет левой, а если вы желаете попасть в какое-то место в зазеркалье, нужно идти прямо в противоположную сторону. В нашем мире скорость это частное от деления расстояния на время, то есть v = S/t. В зазеркальном мире все наоборот! Там v = t/S! Кэрролл был не просто сказочником, а математиком, рассказывающим сказку, и смог предвосхитить Эйнштейна. "Самое удивительное было то, что деревья не бежали, как следовало ожидать, им навстречу; как ни стремительно неслись Алиса и Королева, они не оставляли их позади... Сложно двигаться в зазеркальном мире тому, кто привык к законам "предзеркалья". Это следствие закона движения, приведенного выше, - при большой скорости время велико, а расстояние мало. Чем выше скорость, тем меньше пройденное расстояние. Неудивительно, что пространство, имеющее такие законы, представляется загадочным.
математика зазеркалья
v = S/t ?
v = t/S !
Слайд 5
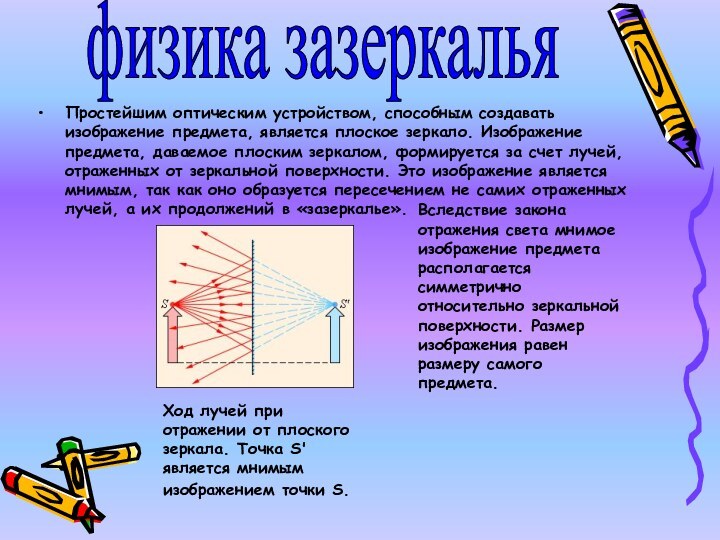
Простейшим оптическим устройством, способным создавать изображение предмета, является
плоское зеркало. Изображение предмета, даваемое плоским зеркалом, формируется за
счет лучей, отраженных от зеркальной поверхности. Это изображение является мнимым, так как оно образуется пересечением не самих отраженных лучей, а их продолжений в «зазеркалье».
физика зазеркалья
Ход лучей при отражении от плоского зеркала. Точка S' является мнимым изображением точки S.
Вследствие закона отражения света мнимое изображение предмета располагается симметрично относительно зеркальной поверхности. Размер изображения равен размеру самого предмета.
Слайд 6
Рассмотрим, как располагаются источник света и его мнимое
изображение относительно зеркала.
Укрепим на подставке кусок плоского стекла в
вертикальном положении. Поставив перед стеклом зажжённую свечу, мы увидим в стекле, как в зеркале, изображение свечи. Возьмём теперь вторую такую же, но незажжённую свечу и расположим её по другую сторону стекла. Передвигая вторую свечу, найдём такое положение, при котором вторая свеча будет казаться тоже зажжённой. Это значит, что незажжённая свеча находится на том же месте, где наблюдается изображение зажжённой свечи. Измерив расстояния от свечи до стекла и от её изображения до стекла, убедимся, что эти расстояния одинаковы. Таким образом, мнимое изображение предмета в плоском зеркале находится на таком же расстоянии от зеркала, на каком находится сам предмет. Предмет и его изображение в зеркале представляют собой не тождественные, а симметричные фигуры.
Отражение в плоском зеркале
Слайд 7
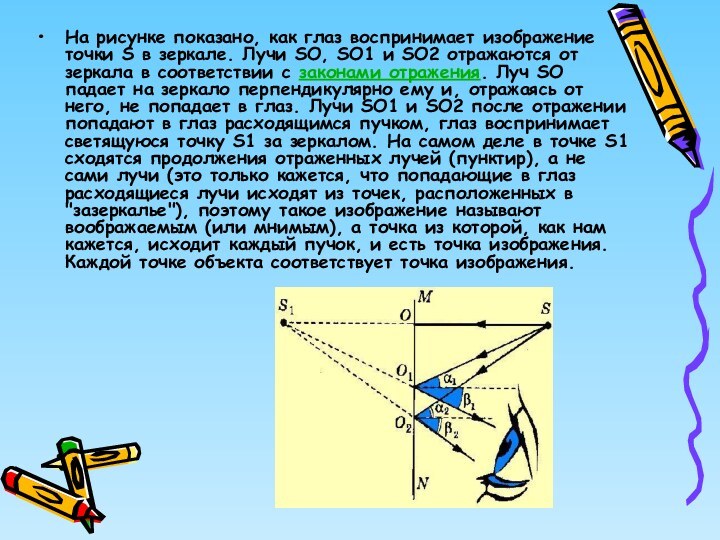
На рисунке показано, как глаз воспринимает изображение точки
S в зеркале. Лучи SО, SО1 и SО2 отражаются
от зеркала в соответствии с законами отражения. Луч SО падает на зеркало перпендикулярно ему и, отражаясь от него, не попадает в глаз. Лучи SО1 и SО2 после отражении попадают в глаз расходящимся пучком, глаз воспринимает светящуюся точку S1 за зеркалом. На самом деле в точке S1 сходятся продолжения отраженных лучей (пунктир), а не сами лучи (это только кажется, что попадающие в глаз расходящиеся лучи исходят из точек, расположенных в "зазеркалье"), поэтому такое изображение называют воображаемым (или мнимым), а точка из которой, как нам кажется, исходит каждый пучок, и есть точка изображения. Каждой точке объекта соответствует точка изображения.
Слайд 8
Если два плоских зеркала расположены под углом φ
друг к другу, то количество изображений N источника света,
расположенного между зеркалами, зависит от угла между ними и может быть определено по формуле:
Плоские зеркала, расположенные под углом
друг к другу
Из этой формулы следует, что если угол φ=0º, то изображений источника будет бесконечно много, а если φ=180º, то изображение будет только одно. Соответственно, если φ=90º, то изображений будет 3, и т.д.
Слайд 9
Построение изображений в плоских зеркалах,
расположенных под углом друг
к другу
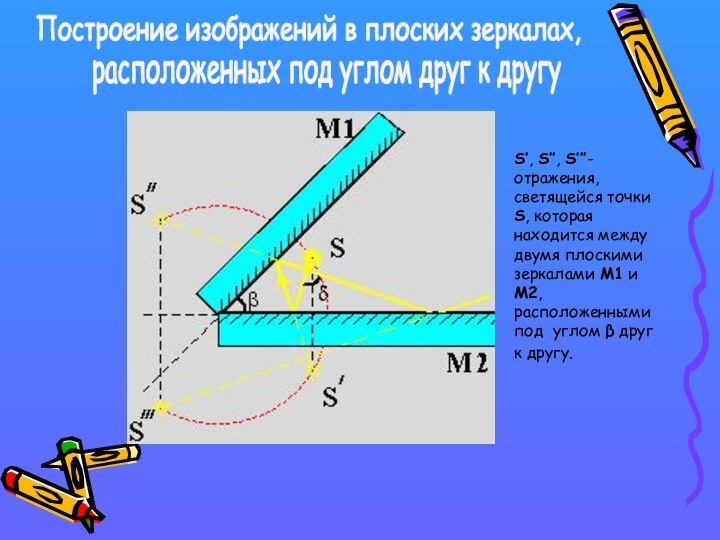
S′, S″, S′″- отражения, светящейся точки S, которая
находится между двумя плоскими зеркалами M1 и M2, расположенными под углом β друг к другу.
Слайд 10
Мы даже не замечаем, что постоянна используем плоские
зеркала в обиходе начиная от маленьких зеркал на точилках
и заканчивая большими трюмо.
Благодаря отражению светового луча, от плоского зеркала можно осуществлять световую сигнализацию. Приемник излучения улавливает отраженный луч. Если этого не происходит (что-то помешало ходу светового луча), то срабатывает тревога.
Прямые зеркала используются в перископах подводных лодок. Это позволяет наблюдать из под воды за тем, что происходит на поверхности.
Применение плоских зеркал
Многократные отражения света параллельными зеркалами используется в интерферометрах Фабри-Перо, где зеркалами служат параллельные кварцевые пластины с нанесенными на них металлическими или многослойными диэлектрическими отражающими покрытиями.
Слайд 11
Сферическим зеркалом называют зеркально отражающую поверхность, имеющую форму
сферического сегмента. Центр сферы, из которой вырезан сегмент, называют
оптическим центром зеркала (с). Вершину сферического сегмента называют полюсом (о). Прямая, проходящая через оптический центр и полюс зеркала, называется главной оптической осью (ос) сферического зеркала. Главная оптическая ось выделена из всех других прямых, проходящих через оптический центр, только тем, что она является осью симметрии зеркала.
Сферические зеркала
Слайд 12
Сферические зеркала бывают вогнутыми и выпуклыми. Если на
вогнутое сферическое зеркало падает пучок лучей, параллельный главной оптической
оси, то после отражения от зеркала лучи пересекутся в точке, которая называется главным фокусом зеркала F. Расстояние от фокуса до полюса зеркала называют фокусным расстоянием и обозначают той же буквой F.
Слайд 13
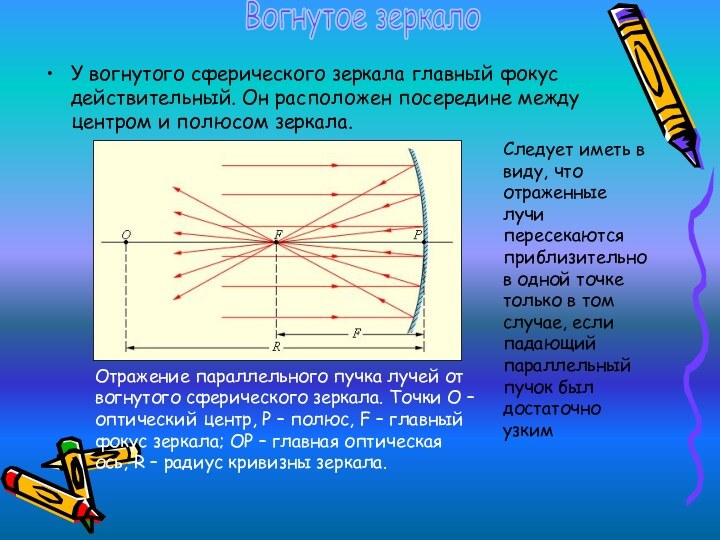
У вогнутого сферического зеркала главный фокус действительный. Он
расположен посередине между центром и полюсом зеркала.
Отражение параллельного
пучка лучей от вогнутого сферического зеркала. Точки O – оптический центр, P – полюс, F – главный фокус зеркала; OP – главная оптическая ось, R – радиус кривизны зеркала.
Следует иметь в виду, что отраженные лучи пересекаются приблизительно в одной точке только в том случае, если падающий параллельный пучок был достаточно узким
Вогнутое зеркало
Слайд 14
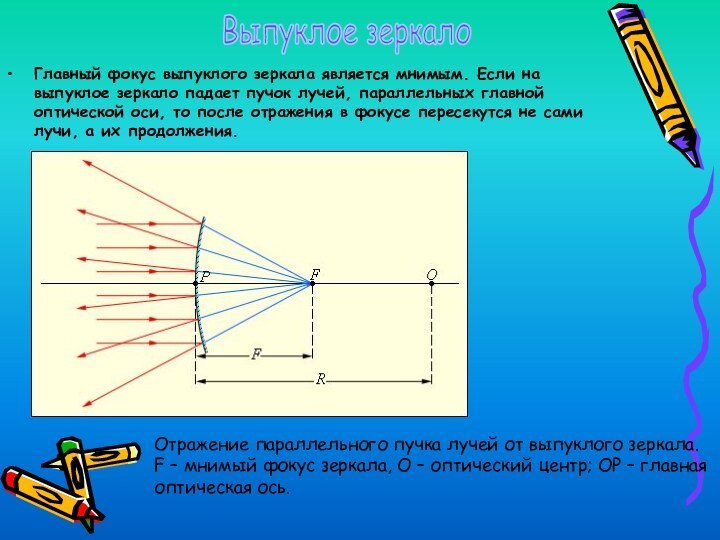
Главный фокус выпуклого зеркала является мнимым. Если на
выпуклое зеркало падает пучок лучей, параллельных главной оптической оси,
то после отражения в фокусе пересекутся не сами лучи, а их продолжения.
Отражение параллельного пучка лучей от выпуклого зеркала. F – мнимый фокус зеркала, O – оптический центр; OP – главная оптическая ось.
Выпуклое зеркало
Слайд 15
Фокусным расстояниям сферических зеркал приписывается определенный знак:
для
вогнутого зеркала и :
для выпуклого зеркала,
где R –
радиус кривизны зеркала.
Фокусное расстояние
Слайд 16
Изображение какой-либо точки A предмета в сферическом зеркале
можно построить с помощью любой пары стандартных лучей:
луч
AOC, проходящий через оптический центр зеркала; отраженный луч COA идет по той же прямой;
луч AFD, идущий через фокус зеркала; отраженный луч идет параллельно главной оптической оси;
луч AP, падающий на зеркало в его полюсе; отраженный луч симметричен с падающим относительно главной оптической оси.
луч AE, параллельный главной оптической оси; отраженный луч EFA1 проходит через фокус зеркала.
Построение изображения в вогнутом сферическом зеркале
Слайд 17
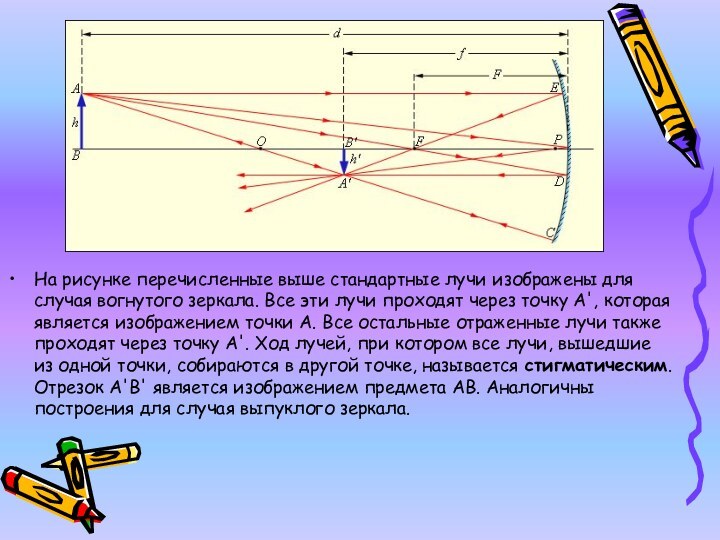
На рисунке перечисленные выше стандартные лучи изображены для
случая вогнутого зеркала. Все эти лучи проходят через точку
A', которая является изображением точки A. Все остальные отраженные лучи также проходят через точку A'. Ход лучей, при котором все лучи, вышедшие из одной точки, собираются в другой точке, называется стигматическим. Отрезок A'B' является изображением предмета AB. Аналогичны построения для случая выпуклого зеркала.
Слайд 18
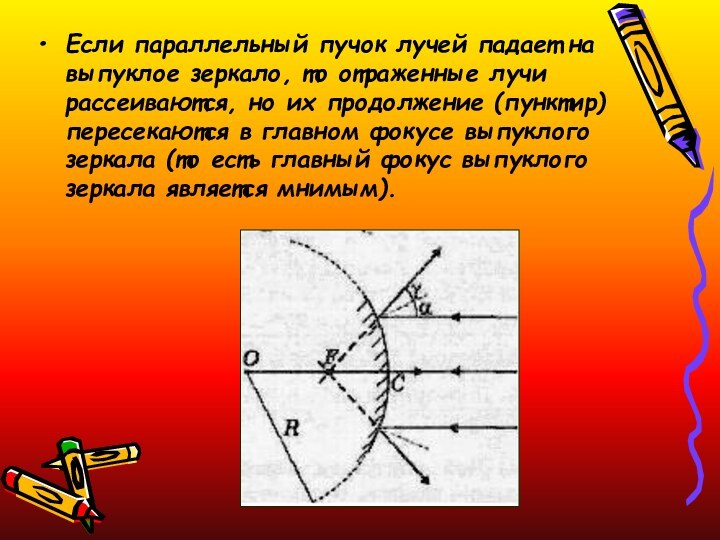
Если параллельный пучок лучей падает на выпуклое зеркало,
то отраженные лучи рассеиваются, но их продолжение (пунктир) пересекаются
в главном фокусе выпуклого зеркала (то есть главный фокус выпуклого зеркала является мнимым).
Слайд 19
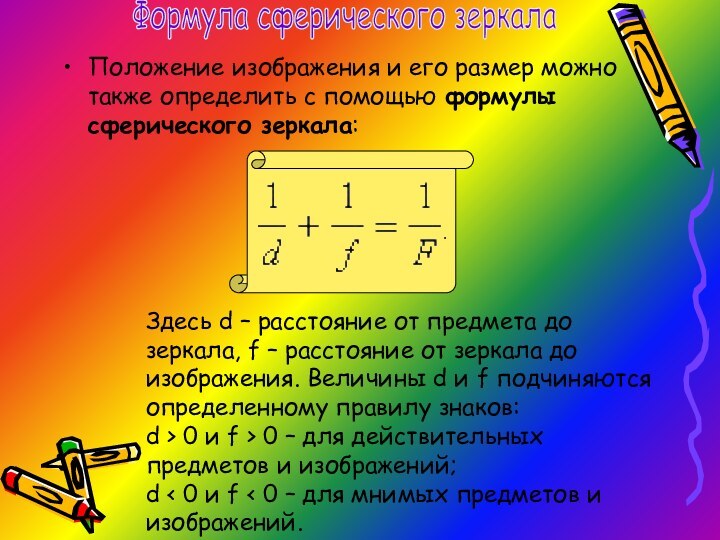
Положение изображения и его размер можно также определить
с помощью формулы сферического зеркала:
Здесь d – расстояние
от предмета до зеркала, f – расстояние от зеркала до изображения. Величины d и f подчиняются определенному правилу знаков:
d > 0 и f > 0 – для действительных предметов и изображений;
d < 0 и f < 0 – для мнимых предметов и изображений.
Формула сферического зеркала
Слайд 20
Линейное увеличение сферического зеркала Γ определяется как отношение
линейных размеров изображения h' и предмета h.
Величине h'
удобно приписывать определенный знак в зависимости от того, является изображение прямым (h' > 0) или перевернутым (h' < 0). Величина h всегда считается положительной. При таком определении линейное увеличение сферического зеркала выражается следующей формулой:
Линейное увеличение сферического зеркала
Слайд 21
Если поместить в фокус параболического зеркала небольшую лампу,
то вследствие обратимости лучей весь падающий на зеркало от
лампы расходящийся световой пучок отразится в виде пучка параллельных лучей.
При конструировании лазеров рубиновый стержень и лампу оптической накачки располагают в фокусах зеркального оптического цилиндра. В этом случае свет, излученный лампой весь попадет на стержень.
Применение сферических зеркал
Вогнутые зеркала применяются в телескопах- рефлекторах, которые используют для изучения глубин вселенной
Слайд 22
Рассмотрим обычный процесс отражения. Существует падающая волна, отражающая
поверхность и отраженная волна. Как известно, падающая волна не
идентична отраженной. Отраженная волна – это совсем другая волна с другими свойствами и характеристиками. Проще говоря, что-то осталось внутри зеркала, а что-то пришло к нам из зазеркалья. Следует учесть также и тот момент, что падающая волна –излучение не только в видимом диапазоне частот. Человек излучает еще и в невидимом диапазоне, поэтому отраженная волна – это не только видимый свет. Так что если изменения между падающей и отраженной волной происходят в невидимой части спектра, то человек, смотрящийся в зеркало их попросту не замечает.
Процесс отражения
Слайд 23
На параметры отраженного света влияют тончайшие (вплоть до
мономолекулярных) поверхностные слои зеркала и их особенности. Любое зеркало
имеет свой набор дефектов, потому что зеркала делают поточным методом, и никто еще не создал зеркало с идеально отражающей поверхностью, с абсолютно точно выверенным составом отражающего слоя, с тщательно проверенной на наличие дефектов кристаллической решеткой, идеально гладкое и бескрайнее (чтобы исключить дефекты края). А каждый дефект влияет на «обработку» поглощенной световой волны. Значит, чем больше дефектов, тем больше отличается отраженная волна от падающей. А небольшое изменение падающей волны может привести к большим изменениям волны отраженной.
Слайд 24
Возможно, обыкновенное зеркало, знакомое и привычное нам с
детства, это первый волшебный предмет, созданный человеком. Свойство показывать
окружающий мир и, прежде всего, то, что мы не можем видеть - свое собственное лицо, разве это не чудо? Но существуют зеркала, обладающие свойствами, в какие трудно поверить, пока не увидишь их собственными глазами.
Еще давно было известно, что на территории Китая в древних храмах хранятся зеркала, которые могут показывать, где живет Будда. Если на такие зеркала направить солнце, а отраженный «зайчик» - на белую стену или лист бумаги, то на них появится изображение, которого нет на полированной лицевой стороне зеркала, и если не знать секрет, то этой стороной вполне можно пользоваться как обычным зеркалом.
Волшебные зеркала
Слайд 25
В начале XX века в Китае были
обнаружены зеркала, у которых рисунок в "солнечном зайчике" не
соответствовал рельефу на обратной стороне зеркала! Например, в одном буддийском храме хранилось зеркало, на тыльной стороне которого изображена луна, сияющая над морем, а в отраженном солнечном луче на стене храма возникала фигура Будды в цветке лотоса.
Слайд 26
Возможные способы производства волшебных зеркал:
1.
При литье более тонкие части зеркала остывают быстрее, чем
толстые, что приводит к деформациям поверхности. Поскольку этот процесс зависит от очень многих факторов, только одно-два из сотни зеркал как бы сами собой становятся "волшебными".
2. На лицевой стороне зеркала гравируется рисунок, который затем заполняется бронзой другого сорта и полируется.
3. На лицевой стороне зеркала вырезается рисунок, затем поверхность покрывается амальгамой ртути и полируется.
4. Рисунок на лицевой стороне зеркала протравливается кислотой или другими химикатами, а затем полируется.
5. Рисунок прорезается на тыльной стороне зеркала, что вызывает появление неровностей при полировке лицевой поверхности.
6. Рисунок штампуется на лицевой стороне зеркала, а затем поверхность полируется.
Слайд 27
Если кто -то захочет сам проникнуть в секрет

волшебных зеркал, то один из путей исследований - это
попытаться самому изготовить волшебное зеркало из... монеты или медали. Ведь отштампованный, а затем сошлифованный рисунок можно увидеть в отраженном свете. И если полировать монету до момента исчезновения рисунка, то, может быть, он снова станет виден в "солнечном зайчике" . Можно шлифовать лицевую сторону монеты до тех пор, пока не начнет проявлять себя рисунок с обратной стороны, и получить "волшебную прозрачную монету", у которой герб России будет "виден" через слой металла. В обоих случаях поверхность монеты должна быть слегка выпуклой, так же как немного выпуклы все волшебные зеркала. При полировке верхнего рисунка не следует прилагать больших усилий. А если попытаться сделать "прозрачную монету", то при шлифовке нужно сильнее давить на обрабатываемую поверхность, особенно в конце работы. Проверять монету следует солнечным лучом, а экран располагать на разных расстояниях от нее.
Слайд 28
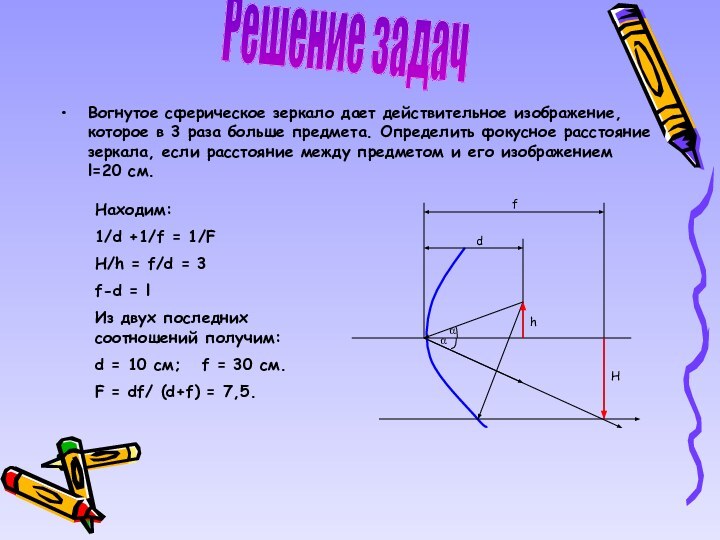
Вогнутое сферическое зеркало дает действительное изображение, которое в
3 раза больше предмета. Определить фокусное расстояние зеркала, если
расстояние между предметом и его изображением l=20 см.
Решение задач
Находим:
1/d +1/f = 1/F
H/h = f/d = 3
f-d = l
Из двух последних соотношений получим:
d = 10 см; f = 30 см.
F = df/ (d+f) = 7,5.
Слайд 29
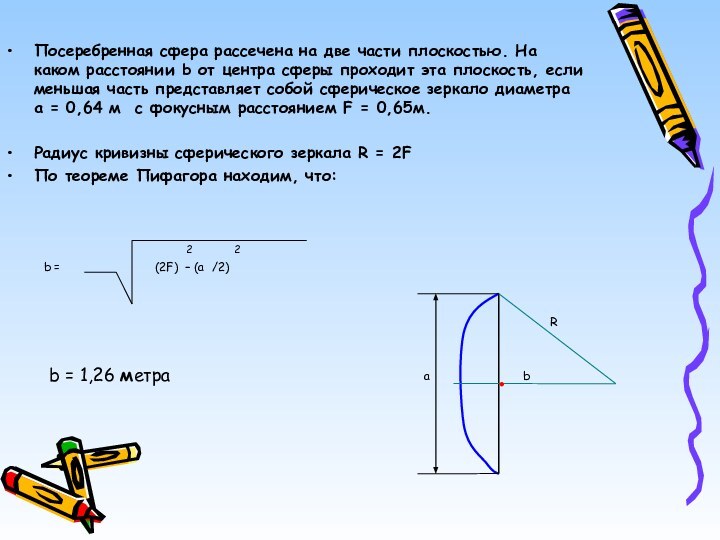
Посеребренная сфера рассечена на две части плоскостью. На
каком расстоянии b от центра сферы проходит эта плоскость,
если меньшая часть представляет собой сферическое зеркало диаметра a = 0,64 м с фокусным расстоянием F = 0,65м.
Радиус кривизны сферического зеркала R = 2F
По теореме Пифагора находим, что:
b = 1,26 метра
Слайд 30
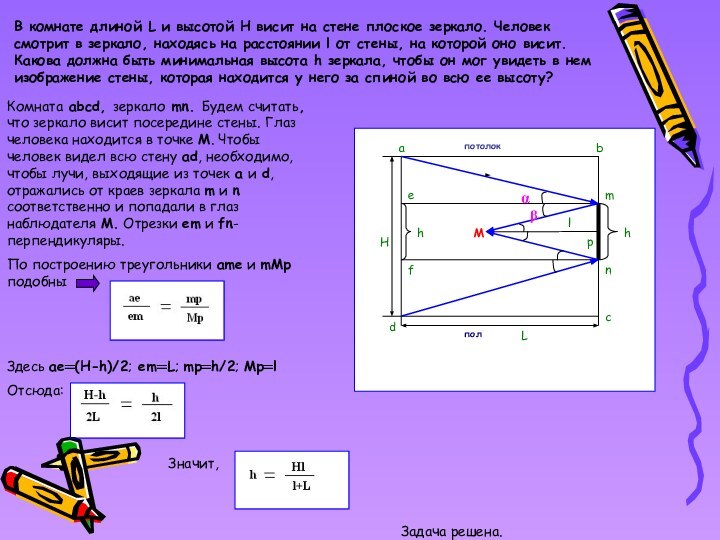
В комнате длиной L и высотой H висит
на стене плоское зеркало. Человек смотрит в зеркало, находясь
на расстоянии l от стены, на которой оно висит. Какова должна быть минимальная высота h зеркала, чтобы он мог увидеть в нем изображение стены, которая находится у него за спиной во всю ее высоту?
Комната abcd, зеркало mn. Будем считать,что зеркало висит посередине стены. Глаз человека находится в точке M. Чтобы человек видел всю стену ad, необходимо, чтобы лучи, выходящие из точек a и d, отражались от краев зеркала m и n соответственно и попадали в глаз наблюдателя M. Отрезки em и fn- перпендикуляры.
По построению треугольники ame и mMp подобны
Здесь ae═(H-h)/2; em═L; mp═h/2; Mp═l
Отсюда:
Значит,
Задача решена.
Слайд 31
Светящаяся точка S расположена на расстоянии r=12см от
линии пересечения двух плоских зеркал mn и mp, расположенных
под углом α=30° друг к другу, на биссектрисе mq этого угла. На каком расстоянии l находятся друг от друга два первых изображения S׳ и S˝этой точки?
d= d׳, т. к. изображение расположено на том же расстоянии от зеркала, что и сам предмет.
Так как mq-биссектриса, то SS׳=SS˝
Угол S׳=α/2
Отсюда S׳C- катет в прямоугольном ΔSS׳C- равен (d+d׳)cosα/2= 2dcosα/2
С другой стороны, d=r·sinα/2
Таким образом, S׳C=2r·sinα/2·cosα/2= r·sinα
l = 2S׳C = 2r·sinα
l = 2·12·sin30°= 12см.
l=12см.
№1
На каком расстоянии d от вогнутого зеркала с фокусным расстоянием F = 1м необходимо поместить источник света, чтобы его изображение совпало с самим источником?
(ответ: d=2м)
№2
Предмет находится на расстоянии d = 0,48 м от вогнутого зеркала. Зеркало дает действительное изображение предмета с уменьшением k=4. Найти радиус кривизны R зеркала.
(ответ: R=19,2 см)
Задачи
№3
Вогнутое зеркало дает изображение предмета с увеличением k=2. Найти радиус кривизны зеркала R , если расстояние между предметом и изображением a=18 см.
(ответ: R=24 см)
№4
Пучок лучей от бесконечно удаленного источника света падает на экран, имеющий отверстие диаметра d=7см. Плоскость экрана перпендикулярна к лучам. На расстоянии a=68 см за экраном расположено вогнутое зеркало с фокусным расстоянием F=0,28 м, главная оптическая ось которого совпадает с осью пучка. Найдите диаметр D светлого круга на экране.
(ответ: D=0,1м)
Слайд 34
№5
Два плоских зеркала расположены под углом друг к
другу. Между ними помещен точечный источник света S. Изображение
источника света S в первом зеркале находится на расстоянии d1 =6см, а во втором зеркале d2 =8см от источника S. Найти угол φ между зеркалами, если расстояние между изображениями l=10см.
( ответ: 90°)