Слайд 2
Задача 1
Укажите наибольшее число, двоичная запись которого содержит
ровно три значащих нуля и две единицы.
Ответ запишите
в десятичной системе счисления.
Решение
1) Значащие нули не могут располагаться в самом начале числа.
Значит, число должно начинаться хотя бы с одной единицы.
2) Чем левее в двоичном числе единица, тем бóльшая степень двойки
ей соответствует. Максимальное значение двоичного числа получится,
если все единицы будут «собраны» в старших разрядах.
3) В записи числа ровно три значащих нуля и две единицы.
Следовательно, число – 5-разрядное. Если все единицы размещаются
в старших разрядах, то это число 110002.
4) Ответ в десятичной форме: 110002 = 24 + 23 = 16 + 8 = 2410.
Ответ: 24.
Слайд 3
Задача 2
Даны числа, записанные в разных системах счисления
и в том числе
в виде арифметических выражений. Укажите
среди них то, в двоичной записи которого имеется ровно четыре единицы. Если таких чисел несколько,
то укажите наибольшее из них.
1) B816 2) 1101112 3) 2168 + 3516 4) 2910 * 108
Решение
1
B816
184
10111000
4
184
2
1101112
–
110111
5
55
3
2168+3516
142+53=195
11000011
4
195
4
2910*108
29*8=232
11101000
4
232
4
4
4
Наибольшее из трех чисел – 2910 * 108
Слайд 4
Задача 3
Между населенными пунктами A, B, C, D,
E, F, Z построены дороги
с односторонним движением. В
таблице указана протяженность каждой дороги. Отсутствие числа в таблице означает, что прямой дороги между пунктами нет. Например, из А в В есть дорога длиной 4 км, а из В в А дороги нет.
Сколько существует таких маршрутов из A в Z, которые проходят через
6 и более населенных пунктов? Пункты A и Z при подсчете учитывать.
Два раза проходить через один пункт нельзя.
Слайд 5
Задача 3
Решение
Строим по таблице ориентированный граф:
Слайд 6
Задача 3
Рисуем дерево всех возможных путей из А
в Z, при этом конечные точки маршрута (Z) выделяем
цветом и рамкой. Не забываем о запрете
на повторное посещение вершин: обратный путь FE нельзя рисовать
в тех ветвях дерева, где уже где-то ранее фигурировали буквы E и F
(такие ветви в графе, где из Е допускается только один путь в Z, отметим синими пунктирными стрелками):
Слайд 7
Задача 3
Остается подсчитать количество ветвей в этом графе,
включающих в себя
6 и более вершин (т.е. когда
запись последовательности имен проходимых вершин состоит из 6 и более букв).
Это ветви (пути):
ABCDFZ,
ABCDFEZ,
ABCDEZ,
ABCDEFZ,
ACDFEZ,
ACDEFZ.
Всего – 6 путей.
Ответ: 6.
АZ
AC
AB
ACZ
ACD
ACDZ
ACDF
ACDE
ACDFZ
ACDFEZ
ACDEZ
ACDEFZ
ABC
ABCZ
ABCD
ABCDZ
ABCDF
ABCDE
ABCDFZ
ABCDFEZ
ABCDEZ
ABCDEFZ
Слайд 8
Задача 4
Каждое из логических выражений F и G
содержит 6 переменных.
В таблицах истинности выражений F и
G есть ровно 10 одинаковых строк, причем ровно в 5 из них в столбце значений стоит 1.
Сколько строк таблицы истинности для выражения F G содержит 1
в столбце значений?
Слайд 9
Задача 4
Решение
1) В каждом из логических выражений имеется
6 переменных, следовательно,
для каждого выражения возможно
26 = 64 различных набора значений
переменных.
2) В таблицах истинности выражений есть 10 одинаковых строк
(когда обе функции имеют значение 1 или значение 0).
Значит, строк, в которых значения функций не совпадают, будет 64 – 10 = 54.
3) Выражение F G равно 1, если хотя бы одно из значений (F или G)
равно единице, и равно нулю тогда и только тогда, когда оба значения
(и F, и G) равны нулю. Cреди одинаковых строк в таблицах истинности
F и G есть ровно 5 строк, в которых значения равны 1. Значит, таких строк,
где и для F, и для G значения равны нулю, будет 10 – 5 = 5 штук.
Слайд 10
Задача 4
Решение
4) Итак, имеем:
54 строки, в которых
значения F и G различны (одно равно 0,
другое равно 1), т.е. значение выражения F G равно 1;
5 строк, в которых значения F и G одинаковы и равны 1,
т.е. значение выражения F G также равно 1;
5 строк, в которых значения F и G одинаковы и равны 0,
т.е. значение выражения F G равно 0.
Условиям задачи соответствует, таким образом, 54 + 5 = 59 строк.
Ответ: 59.
Слайд 11
Задача 5
Для групповых операций с файлами используются маски
имён файлов.
Маска представляет собой последовательность букв, цифр и
прочих допустимых в именах файлов символов, в которых также могут встречаться следующие символы:
Символ «?» (вопросительный знак) означает ровно один произвольный символ.
Символ «*» (звёздочка) означает любую последовательность символов
произвольной длины, в том числе пустую последовательность.
В каталоге находится 6 файлов:
maverick.map maverick.mp3 taverna.mp4
revolver.mp4 vera.mp3 zveri.mp3
Ниже представлено восемь масок. Сколько из них таких, которым соответствуют ровно три файла из данного каталога?
Слайд 12
Задача 5
Решение
1) Маска *ver*.mp* предполагает, что где-то в
имени файла содержится набор
символов ver, а
расширение начинается с символов mp. Значит, такая
маска отберет файлы maverick.mp3, taverna.mp4, revolver.mp4, vera.mp3,
zveri.mp3 – всего 5 файлов. Значит, эта маска нам не годится.
6 файлов:
maverick.map maverick.mp3 taverna.mp4
revolver.mp4 vera.mp3 zveri.mp3
2) Маска *?ver?*.mp? отличается от предыдущей тем, что до и после
символов ver обязательно должны стоять минимум по одному символу,
а в расширении после символов mp может быть только один символ.
Значит, такая маска отберет файлы maverick.mp3, taverna.mp4 и zveri.mp3
(а имена revolver.mp4 и vera.mp3 не удовлетворяют этой маске, так как
в них группа символов ver располагается с краю имен). Всего – 3 файла.
Значит, эта маска подходит.
Слайд 13
Задача 4
Решение
3) Маска ?*ver*.mp?* – минимум один символ
должен быть перед ver,
а в
расширении после mp должно быть не менее одного символа.
Такая маска отберет файлы maverick.mp3, taverna.mp4, revolver.mp4
и zveri.mp3 – 4 файла. Данная маска не годится.
6 файлов:
maverick.map maverick.mp3 taverna.mp4
revolver.mp4 vera.mp3 zveri.mp3
4) Маска *v*r*?.m?p* – не обращая внимания на маску имени, заметим:
в расширении между m и p должен стоять хотя бы один какой-то символ.
А у нас этому условию соответствует единственный файл maverick.map.
Значит, эта маска тоже не годится.
Слайд 14
Задача 4
Решение
5) Маска ???*???.mp* – ей удовлетворяют файлы
с любыми именами
не менее чем
из 6 букв и с расширениями, начинающимися с mp.
Значит, будут отобраны файлы maverick.mp3, taverna.mp4 и revolver.mp4
(у файлов vera.mp3 и zveri.mp3 имена слишком короткие, а расширение
файла maverick.map не соответствует расширению в маске).
Значит, данная маска тоже подходит.
6 файлов:
maverick.map maverick.mp3 taverna.mp4
revolver.mp4 vera.mp3 zveri.mp3
6) Маска ???*???.m* – отличается от предыдущей тем, что здесь расширение
может быть любым, лишь бы оно начиналось с m. Тогда в дополнение
к файлам maverick.mp3, taverna.mp4 и revolver.mp4 в подборку попадет
и файл maverick.map. Всего – 4 файла. Значит, эта маска не годится.
Слайд 15
Задача 4
Решение
7) Маска *a*.*a* – соответствует любым файлам,
у которых и в имени,
и
в расширении есть хотя бы одна буква a. Этому условию соответствует
только один файл – maverick.map. Значит, эта маска тоже не годится.
6 файлов:
maverick.map maverick.mp3 taverna.mp4
revolver.mp4 vera.mp3 zveri.mp3
8) Маска *a*.*p* – здесь в имени требуется хотя бы одна буква a,
а в расширении – хотя бы одна буква p. Этому условию соответствуют
файлы: maverick.map, maverick.mp3, taverna.mp4 и vera.mp3.
В этой подборке 4 файла, значит, данная маска тоже не годится.
Итого нам подошло две маски – *?ver?*.mp? и ???*???.mp*.
Ответ: 2.
Слайд 16
Задача 6
Автомат получает на вход четырехзначное число. По
этому числу строится новое число по следующим правилам.
1. Складываются первая и вторая, а также третья и четвертая цифры
исходного числа.
2. Полученные два числа записываются друг за другом в порядке возрастания
(без разделителей).
Пример. Исходное число: 6531. Суммы: 6+5 = 11, 3+1 = 4. Результат: 411.
Укажите наибольшее число, в результате обработки которого автомат выдаст число 1113.
Слайд 17
Задача 6
Решение
1) Числа (по умолчанию) десятичные. Значит, суммы
цифр могут быть
в диапазоне от 0
(0+0) до 18 (9+9).
2) Автомат выдал число 1113. Значит, оно состоит из двух значений сумм,
записанных по возрастанию: 11 и 13.
3) Число 11 может быть суммой цифр: 2+9, 3+8, 4+7 или 5+6.
Число 13 может быть суммой цифр: 4+9, 5+8, 6+7.
Значит, пары цифр в исходном числе могут быть такими:
одна пара – 29, 92, 38, 83, 47, 74, 56, 65 и другая пара – 49, 94, 58, 85, 67, 76
(соответствующие цифры могут меняться местами в суммах).
4) Наибольшим является число, в которое входят наибольшие цифры,
причем они по возможности располагаются слева направо по убыванию
(чем старше разряд, тем больше «вес» цифры). Тогда из доступных наборов
пар цифр выберем две наибольшие (по одной из каждого набора): 92 и 94
и запишем их по убыванию: 9492.
Ответ: 9492.
Слайд 18
Задача 7
В фрагменте базы данных представлены сведения
о
родственных отношениях.
На основании приведенных данных определите, сколько прямых
потомков
(то есть детей
и внуков)
Кривич Л.П. упомянуты
в таблице.
Слайд 19
Задача 7
Решение
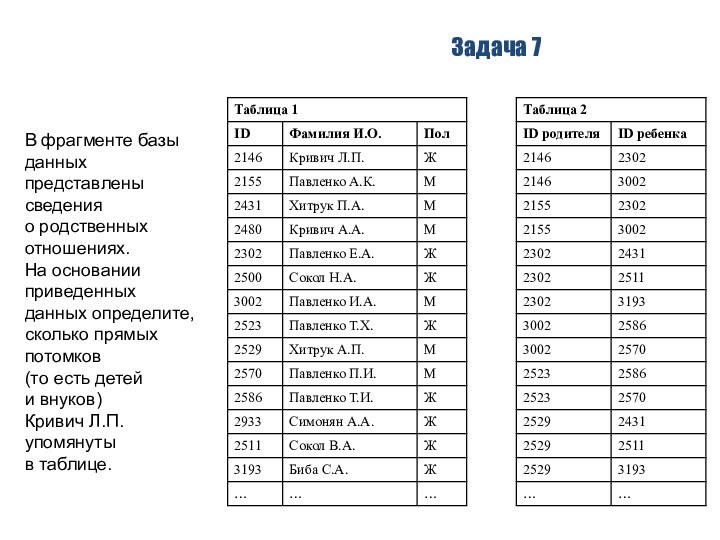
1) В табл. 1 ищем Кривич Л.П.
и определяем ее ID: 2146.
Слайд 20
Задача 7
Решение
2) В правой таблице ищем все пары
ID, в которых первое число (в левой колонке) равно
2146. Для них в правой колонке записаны ID 2302 и 3002.
Это – дети Кривич Л.П.
Слайд 21
Задача 7
Решение
3) В правой таблице ищем все пары
ID, в которых первое число (в левой колонке) равно
2302 или 3002. Это – внуки Кривич Л.П.
Слайд 22
Задача 7
Решение
4) Подсчитываем количество закрашенных в табл. 2
строк: 7
(двое детей и пятеро внуков).
Ответ: 7.
Слайд 23
Задача 8
В ячейке K12 электронной таблицы была записана
некая формула.
Затем ее скопировали в ячейку H15. Тогда
в соответствии с формулой
в ячейке H15 ее значение стало равно произведению значений в ячейках С10
и F7. Укажите, сколько из приведенных ниже высказываний не противоречат сказанному.
1. Значение в ячейке K12 равно a*b, где a – значение ячейки С10,
а b – значение ячейки F7.
2. Значение в ячейке K12 равно a*b, где a – значение ячейки С10,
а b – значение ячейки I4.
3. Значение в ячейке K12 равно a*b, где a – значение ячейки F10,
а b – значение ячейки F4.
4. Значение в ячейке K12 равно a2, где a – значение ячейки F7.
1) 1 2) 2 3) 3 4) 4
Слайд 24
Задача 8
Решение
Высказывание 1. Значение в ячейке K12

равно a*b, где a – значение ячейки С10,
а b – значение ячейки F7.
При копировании формулы из одной ячейки в другую используемые в формуле ячейки не изменяются только в одном случае – если это абсолютные ссылки. Если формула в ячейке K12 имела вид =$С$10*$F$7, то в ячейке H15 формула такой и останется, – что нам и требовалось (произведение значений ячеек
С10 и F7). Значит, первое высказывание условию задачи не противоречит.
Высказывание 2. Значение в ячейке K12 равно a*b, где a – значение ячейки С10, а b – значение ячейки I4
При копировании формулы первый сомножитель не изменился (значит, ссылка на данную ячейку – абсолютная), а второй сомножитель при переносе формулы из ячейки K12 в ячейку H15 должен был измениться с I4 на F7.
Если второй сомножитель был выражен в формуле относительной ссылкой,
то при таком копировании формулы буква должна «уменьшиться» на три позиции латинского алфавита, а цифра – наоборот, увеличиться на 3. Что мы
и наблюдаем. Значит, формула в ячейке K12 имела вид =$С$10*I4, а в ячейке H15 стала такой: =$С$10*F7. Значит, второе высказывание условию задачи тоже не противоречит.
Слайд 25
Задача 8
Решение
Высказывание 3. Значение в ячейке K12 равно
a*b, где a – значение ячейки F10,
а b – значение ячейки F4
После копирования формулы изменились оба сомножителя: первый в ячейке K12 соответствовал ячейке F10, а после копирования формулы в H15 предположительно изменился на C10. Второй сомножитель должен был измениться с F4 на F7. Может ли такое быть? Да, если в первом сомножителе было относительное имя столбца и абсолютный номер строки, а во втором – наоборот, относительный номер строки и абсолютное имя столбца.
То есть, если формула в ячейке K12 была записана как =F$10*$F4, то в ячейке H15 она примет вид: =С$10*$F7 (в относительных частях этих смешанных ссылок буква «уменьшается» на три позиции латинского алфавита, а цифра увеличивается на 3). В любом случае третье высказывание тоже непротиворечиво.
Слайд 26
Задача 8
Решение
Высказывание 4. Значение в ячейке K12 равно
a2, где a – значение ячейки F7.
Наконец, может ли
быть, что произведение до копирования формулы было квадратом?
Возведение в квадрат – это умножение значения само на себя. Значит,
в четвертом высказывании речь идет о следующем изменении ссылок
на ячейки-сомножители при копировании формулы из K12 в H15: произведение F7 на F7 превратилось в произведение С10 на F7.
В этом случае одна из «исходных» ссылок на F7 была абсолютной, а вторая – относительной: если формула в ячейке K12 имела вид, например, =&F$7*F7, то в ячейке H15 она станет такой: =$F$7*С10 (во второй ссылке буква «уменьшается» на три позиции латинского алфавита, а цифра увеличивается на 3). Поэтому четвертое высказывание тоже не содержит никаких противоречий с условием задачи.
Вывод: не противоречащих высказываний в данном случае – четыре (т.е. все имеющиеся).
Ответ 4
Слайд 27
Задача 9
Производилась двухканальная (стерео) звукозапись с частотой дискретизации
64 кГц и 24-битным разрешением. В результате был получен
файл размером 480 Мбайт, сжатие данных не производилось. Определите приблизительно, сколько времени (в минутах) проводилась запись. В качестве ответа укажите ближайшее к времени записи целое число, кратное 10.
Слайд 28
Задача 9
Решение
1) Разрешение равно 24 бит.
2) Частота дискретизации
равна 64 кГц – 64000 измерений в секунду.
3) Длительность
записи (в секундах) примем равной x.
4) Запись двухканальная – объем информации умножается на 2.
5) Результирующий объем файла равен 480 Мб, или 480223 бит.
(Не забываем, что все расчеты ведутся в битах и в секундах.)
6) Составляем уравнение: 24 64000 x 2 = 480223.
Для удобства вычислений по возможности выделяем степени двойки.
Решаем уравнение, получаем: x = 1310,72 (секунд).
7) Переводим x в минуты: x 1311 / 60 21,85 (минут).
8) Округляем до ближайшего значения, кратного 10: x 21,85 20 (минут).
Ответ: 20.
Слайд 29
Задача 10
По каналу связи передаются сообщения, содержащие только
4 буквы П, О, С, Т. Для передачи используется
двоичный код, допускающий однозначное декодирование. Для букв Т, О, П используются такие кодовые слова:
Т – 101, О – 0, П – 100.
Укажите кратчайшее кодовое слово для буквы С, при котором код будет допускать однозначное декодирование. Если таких кодов несколько,
укажите код с наименьшим числовым значением.
Слайд 30
Задача 10
Решение
Условие Фано:
Неравномерный код может быть однозначно декодирован,
если никакой из кодов не совпадает с началом (префиксом)
какого-либо другого,
более длинного кода.
Таким образом, требуется найти кратчайший код, не совпадающий
ни с одним имеющимся кодом или с началом ни одного из имеющихся кодов
(Т – 101, О – 0, П – 100). Поиск решения ведем простым перебором
от однобитовых кодов к кодам большей разрядности:
код 0 – не годится (совпадает с кодом буквы О);
код 1 – не годится (совпадает с началом кодов 100 и 101);
код 10 – не годится (совпадает с началом кодов 100 и 101);
код 11 – не совпадает с началом никакого из имеющихся кодов
и ни с одним из имеющихся кодов. Следовательно, это и есть ответ.
Ответ: 11.
Слайд 31
Задача 11
На числовой прямой даны да отрезка: P
= [43, 49] и Q = [44, 53].
Укажите наибольшую
возможную длину отрезка А, для которого формула
( (x A) (x P) ) (x Q)
тождественно истинна, то есть принимает значение 1 при любом значении переменной x.
Слайд 32
Задача 11
Решение
1) Как обычно, заменяем высказывания логическими переменными:
a = (x A), p = (x P), q = (x Q).
Тогда исходное логическое выражение принимает вид:
( a p ) q
2) Избавимся от операции следования, использовав закон Моргана
(x y = x y):
( a p ) q = a p q.
3) Требуется тождественное равенство этого выражения единице
на все числовой оси. При этом помним, что значения логических
переменных равны 1 в пределах соответствующих отрезков
и 0 – вне их (причем границы входят в отрезки).
Слайд 33
Задача 11
Решение
Анализируем полученное уравнение a p
q = 1:
переменные соединены операцией ИЛИ, следовательно,
результат 1
будет автоматически обеспечен, если хотя бы одна из переменных –
p или q – равна 1 (то есть везде, где числовая прямая «накрыта»
хотя бы одним отрезком – P или Q);
там, где нет ни отрезка P, ни отрезка Q (т.е. переменные p и q обе равны 0),
для обеспечения истинности результата должна быть равна 1 переменная
a, или, соответственно, переменная a должна быть равна 0 (отрезка A
не должно быть нигде, где нет ни отрезка P, ни отрезка Q).
Слайд 34
Задача 11
Решение
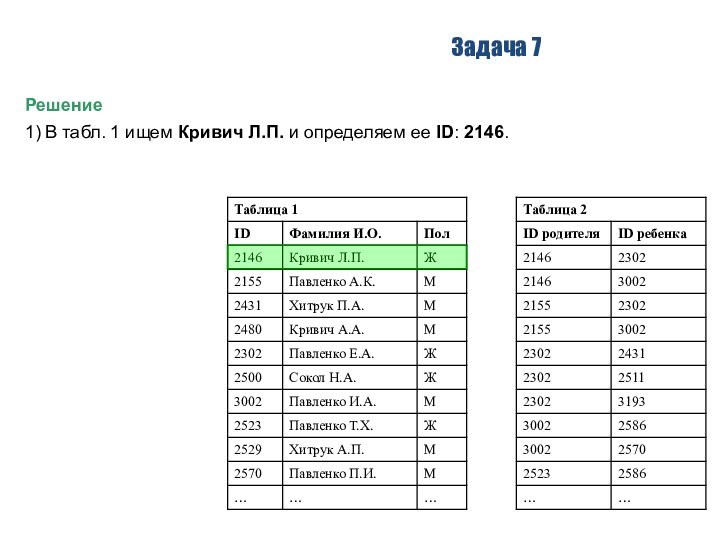
4) Рисуем числовую прямую и изображаем на
ней отрезки P и Q:
5) Теперь очевидно, как расположить
на этой числовой прямой отрезок A,
чтобы он нигде «не высовывался» за пределы области, закрытой
хотя бы одним отрезком P или Q:
Слайд 35
Задача 11
Решение
6) А теперь нужно правильно вычислить длину
полученного отрезка A,
помня, что речь идет
о прямой натуральных чисел. В данном случае
это не имеет особого значения, но в других аналогичных задачах
при выполнении операции отрицания границы отрезка A могут быть
«выколоты» (могут не входить в отрезок), и тогда нужно при вычислении
длины отрезка брать соседние натуральные граничные значения внутри
отрезка. В нашем случае конечные точки 43 и 53 входят в отрезок А.
Теперь вспомним, как вычисляется длина отрезка на сантиметровой линейке, – например, между отметками 1 см и 3 см. Длина этого отрезка равна двум сантиметровым интервалам между указанными отметками на шкале линейки, т.е. вычисляется как разность значений. Точно так же нужно поступить и здесь, поэтому длина отрезка А равна 53 – 43 = 10.
Ответ: 10.
Слайд 36
Задача 12
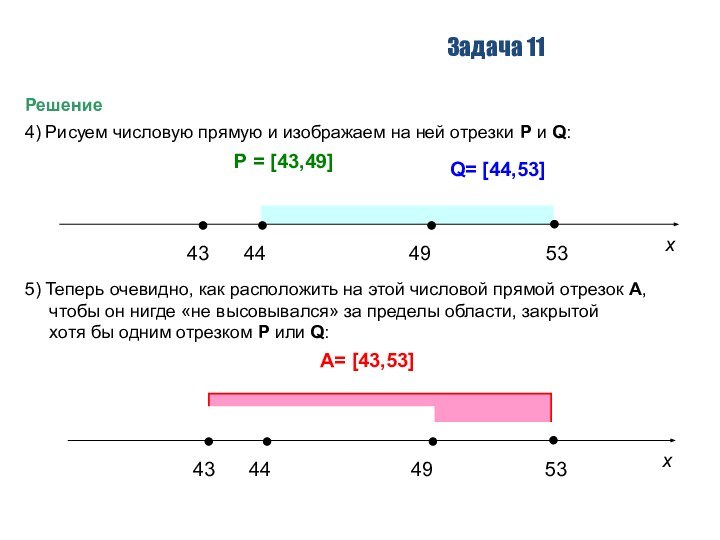
На числовой прямой даны два отрезка: X
= [7,11] и Y = [9,13].
Выберите отрезок Z
такой, что обе приведенные ниже формулы истинны
при любом значении переменной t:
Если таких отрезков окажется несколько, то выберите тот, который имеет наибольшую длину.
1) [8,10] 2) [6,12] 3) [6,14] 4) [8, 18]
Слайд 37
Задача 12
Решение (способ 1)
Сначала соединим обе формулы в
одну через логическую операцию И, поскольку они по условию
должны быть истинными одновременно:
Далее проверяем каждый из отрезков Z, перечисленных в качестве вариантов ответа.
Слайд 38
Задача 12
Решение (способ 1)
1) Z = [8,10]
«Неизменные»
отрезки: [–,7], [7,8], [8,9], [9,10], [10,11], [11,13], [13, ]
Слайд 39
Задача 12
Решение (способ 1)
1) Z = [8,10]
Логическое
выражение:
Есть отрезки,
где логическое выражение обращается в нуль!
Слайд 40
Задача 12
Решение (способ 1)
2) Z = [6,12]
«Неизменные» отрезки:
[–,6], [6,7], [7,9], [9,11], [11,12], [12,13], [13, ]
Слайд 41
Задача 12
Решение (способ 1)
2) Z = [6,12]
Логическое выражение:
Есть
отрезки,
где логическое выражение обращается в нуль!
Слайд 42
Задача 12
Решение (способ 1)
3) Z = [6,14]
«Неизменные» отрезки:
[–,6], [6,7], [7,9], [9,11], [11,13], [13,14], [14, ]
Слайд 43
Задача 12
Решение (способ 1)
3) Z = [6,14]
Логическое выражение:
Логическое
выражение
везде равно единице
Слайд 44
Задача 12
Решение (способ 1)
4) Z = [8,18]
«Неизменные» отрезки:
[–,7], [7,8], [8,9], [9,11], [11,13], [13,18], [18, ]
Слайд 45
Задача 12
Решение (способ 1)
4) Z = [8,18]
Логическое выражение:
Есть
отрезки,
где логическое выражение обращается в нуль!
Слайд 46
Задача 12
Решение (способ 2)
Преобразуем заданные формулы, чтобы избавиться
от логической операции НЕ: нужно заменить знак принадлежности отрезку
на «обратный» знак непринадлежности и наоборот:
Далее порассуждаем, что означает такая запись, учитывая, что по условию
оба заданных логических выражения должны быть истинными одновременно.
Слайд 47
Задача 12
Решение (способ 2)
если t принадлежит отрезку X,
то t обязательно должно принадлежать
и отрезку Z (11
= 1, а 10 = 0); если же t не принадлежит отрезку X,
то принадлежность t отрезку Z нам совершенно безразлична (независимо
ни от чего результатом операции следования будет 1: 00 = 1 и 01 = 1).
если t не принадлежит отрезку Z, то t обязательно не должно принадлежать и отрезку Y (11 = 1, а 10 = 0); если же t принадлежит отрезку Z, то принадлежность t отрезку Y нам тоже безразлична
(00 = 1 и 01 = 1).
Слайд 48
Задача 12
Решение (способ 2)
Из этих рассуждений можно выделить
два «ключевых» критерия,
которые определяют возможность для того или
иного отрезка
быть правильным ответом:
если t принадлежит отрезку X, то t обязательно должно принадлежать
и отрезку Z;
если t не принадлежит отрезку Z, то t обязательно не должно принадлежать
и отрезку Y.
Достаточно по полученным словесным описаниям проверить:
есть ли в получившейся картине расположения отрезков на числовой прямой такие участки, где нарушаются указанные выше «ключевые» правила, т.е.:
если t принадлежит отрезку X и t не принадлежит отрезку Z;
или
если t не принадлежит отрезку Z и t принадлежит отрезку Y.
В нашей «цветовой гамме» это означает, что мы ищем участки, где зеленая штриховка не пересекается с красной или где синяя штриховка
не пересекается с красной.
Слайд 49
Задача 12
Решение (способ 2)
1) Z = [8,10]
По
крайней мере, интервалы [7,8] и [11,13] нарушают правила;
кроме
того, нарушение правил есть и на интервалах [10,11] и [10,13].
Значит, отрезок Z = [8,10] не является правильным ответом.
Слайд 50
6. Игра с отрезками
Решение (способ 2)
2) Z
= [6,12]
Второе правило нарушено для интервала [12,13], и этого
уже достаточно, чтобы отрезок Z = [6,12] не мог быть правильным ответом.
Слайд 51
6. Игра с отрезками
Решение (способ 2)
3) Z
= [6,14]
Нарушений правил нигде нет: красная штриховка везде «с
лихвой» закрывает собой и синюю, и зеленую.
Значит, отрезок Z = [6,14] – это правильный ответ.
Слайд 52
6. Игра с отрезками
Решение (способ 2)
4) Z
= [8,18]
Первое правило нарушено для интервала [7,8], и этого
достаточно, чтобы отрезок Z = [8,18] не был правильным ответом.
Ответ: 3( [6,14])
Слайд 53
Задача 13
При регистрации в компьютерной системе каждому пользователю
выдается пароль, состоящий из 8 символов и содержащий только
заглавные символы нижнего ряда латинской раскладки клавиатуры: Z, X, C, V, B, N, M.
Каждый такой пароль в компьютерной программе записывается минимально возможным и одинаковым целым количеством байт (при этом используют посимвольное кодирование и все символы кодируются одинаковым
и минимально возможным количеством бит).
Определите объем памяти (в байтах), отводимый этой программой для записи 25 паролей. В ответе запишите только число.
Слайд 54
Задача 13
Решение
1) В алфавит входит 7 символов (Z,
X, C, V, B, N, M).
При
такой мощности алфавита для кодирования одного символа требуется
3 бита (23 = 8, а 22 = 4 – недостаточно).
2) Пароль состоит из 8 символов, значит, для их хранения потребуется
83 = 24 бита.
3) Тогда для хранения одного пароля требуется 24/8 = 3 байта.
(Если бы деление выполнялось не нацело, потребовалось бы взять
ближайшее большее целое количество байт.)
4) Для хранения 25 паролей тогда потребуется 253 = 75 байт.
Ответ: 75.
Слайд 55
Задача 14
В программе описан одномерный целочисленный массив с
индексами от 0
до 10. Ниже представлен фрагмент программы,
обрабатывающей данный массив:
s:=0;
n:=10;
for i:=0 to n-1 do begin
s:=s+A[i]-A[i+1];
end;
В начале выполнения этого фрагмента в массиве находились трехзначные натуральные числа, ни одно из которых не делится на 20.
Какое наибольшее значение может иметь переменная s после выполнения данной программы?
Слайд 56
Задача 14
Решение
1) Анализируем алгоритм:
длина массива равна 10;
переменная s обнулена для подсчета суммы;
в цикле выполняется
сложение прежнего значения s с разностью текущего
элемента массива и последующего.
Такое вычисление значения s можно расписать в одну строку в виде:
s = (A[0]-A[1]) + (A[1]-A[2]) + (A[2]-A[3]) + (A[3]-A[4]) + (A[4]-A[5]) + (A[5]-A[6]) + (A[6]-A[7]) + (A[7]-A[8]) + (A[8]-A[9]) + (A[9]-A[10]).
Раскроем скобки и перегруппируем слагаемые:
s = A[0] + (A[1] - A[1]) + (A[2] - A[2]) + (A[3] - A[3]) + (A[4] - A[4]) + (A[5] - A[5]) + (A[6] - A[6]) + (A[7] - A[7]) + (A[8] - A[8]) + (A[9] - A[9]) – A[10].
Как видим, большинство слагаемых сокращается, и получаем:
s = A[0] - A[10].
Слайд 57
Задача 14
Решение
2) При этом требуется, чтобы итоговое значение
s было максимальным.
Когда это возможно, учитывая,
что все числа – трехзначные
и не кратные 20?
Очевидно, уменьшаемое должно быть максимально возможным таким числом, а вычитаемое – минимально возможным.
Всем этим условиям отвечают значения: A[0] = 999, A[10] = 101 (минимально возможное трехзначное число 100 непригодно, так как оно кратно 20).
Тогда значение s (максимально возможное, требуемое в задаче) равно
999 - 101 = 898.
Ответ: 898.
Слайд 58
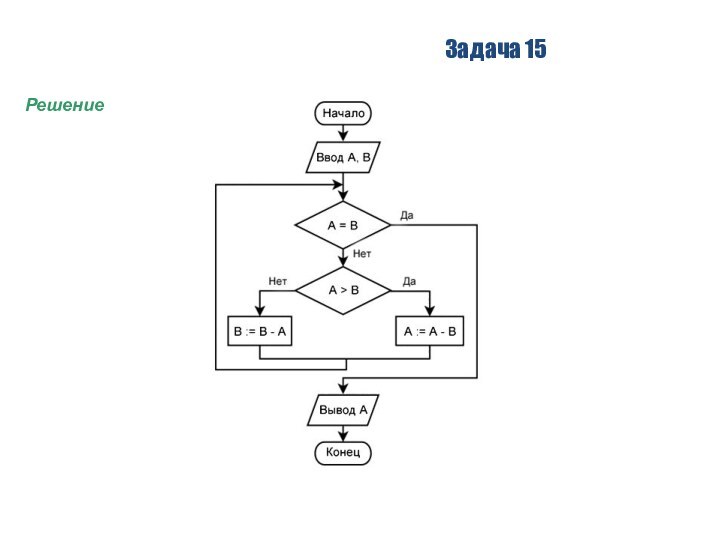
Задача 15
Ниже записан алгоритм. После выполнения алгоритма было
напечатано
3 числа. Первые два напечатанных числа – это
числа 7 и 35.
Какое наибольшее число может быть напечатано третьим?
var x, у, z: integer;
var r, a, b: integer;
begin
readln(x, y);
if у>x then begin z := x; x := y; y := z; end;
a:=x; b;=y;
while b>0 do begin
r := a mod b;
a := b;
b := r;
end;
writeln(a); writeln(x); write(y);
end.
Слайд 59
Задача 15
Решение
Первый ключевой момент – условный оператор:
if у>x
then begin z := x; x := y; y
:= z; end;
Он сортирует заданные числа x и y по убыванию: какие бы два числа
не вводились, после выполнения этого оператора всегда в x будет большее
из двух введенных чисел, а в y –меньшее.
Далее числа x и y дублируются в переменные a и b. Благодаря этому можно затем произвольно изменять значения a и b, но сохранить их исходные значения (в x и y), которые нужны в конце программы для их вывода на экран.
И наконец, самое интересное – цикл while:
while b>0 do begin
r := a mod b;
a := b;
b := r;
end;
Слайд 60
Задача 15
Решение
Попробуем записать запрограммированный здесь алгоритм словесно:
вычисляется
остаток от деления большего числа (a) на меньшее (b),
этот остаток запоминается в r;
большее из бывших двух чисел заменяется на меньшее,
а бывшее меньшее – на вычисленный остаток от деления;
и так – до тех пор, пока получаемое при этом меньшее из двух чисел
(т.е., по сути, последний вычисленный остаток от деления большего числа
на меньшее) не станет равным нулю (меньше нуля остаток от деления,
очевидно, быть не может).
По завершении цикла выводится значение a, которое равно бывшему
на предыдущем шаге цикла меньшему числу.
Слайд 62
Задача 15
Решение
Это знаменитый алгоритм вычисления НОД (наибольшего общего
делителя) двух чисел – алгоритм Евклида, описанный этим греческим
ученым
в его книгах «Начала».
Как он работает?
Берутся два числа, для которых требуется вычислить НОД.
Если они равны, то любое из них – и есть НОД.
Иначе из большего числа вычитается меньшее. Такое вычитание будет
производиться до тех пор, пока полученная разность не окажется меньше,
чем меньшее из имевшихся чисел, тогда далее эти числа меняются местами:
бывшее меньшее становится новым большим, а полученная разность
становится меньшим числом. И так, пока числа не сравняются.
Это – «классический» алгоритм Евклида для нахождения НОД, основанный
на вычитаниях. Но можно его и ускорить, реализовав на основе делений
с остатком.
Слайд 63
Задача 15
Решение
Целую цепочку вычитаний из большего числа меньшего
до тех пор,
пока разность не станет меньше меньшего
из чисел, можно заменить делением большего числа на меньшее с остатком.
Например, цепочка вычитаний: 14 – 3 = 11; 11 – 3 = 8; 8 – 3 = 5; 5 – 3 = 2
дает тот же результат, что и деление с остатком: 14 mod 3 = 2.
А сравнение двух обрабатываемых чисел между собой вполне можно заменить на проверку равенства нулю остатка от их деления друг на друга.
На этих рассуждениях можно сформулировать следующий вариант алгоритма Евклида для нахождения НОД двух чисел:
берется два натуральных числа A и B, где A > B;
вычисляется остаток от их деления друг на друга;
большее число заменяется остатком;
эти действия повторяются, пока не получится нулевой остаток;
тогда предыдущий ненулевой остаток и будет являться НОД
исходных двух чисел.
Слайд 64
Задача 15
Решение
Получаем следующий «модифицированный» алгоритм Евклида с делением.
Берется
два натуральных числа A и B, где A >
B. Затем в цикле:
вычисляется остаток от деления A на B;
большее число заменяется меньшим;
меньшее число заменяется остатком;
эти действия повторяются, пока не получится нулевой остаток;
тогда предыдущий ненулевой остаток и будет являться НОД
исходных двух чисел.
Слайд 65
Задача 15
Решение
Аналогия с ранее проанализированным алгоритмом очевидна.
Таким образом,
в заданном тексте программы фрагмент:
while b>0 do begin
r := a mod b;
a := b;
b := r;
end;
это вычисление НОД двух чисел a и b (т.е. по сути – чисел x и y), а в конце программы сначала выводится найденное значение НОД, а потом – сами исходные числа.
Слайд 66
Задача 15
Решение
Программа, согласно условию, выводила числа 7 и
35 плюс какое-то неизвестное третье число, которое предлагается определить.
Значит, в данном случае НОД равен 7, а одно из чисел равно 35:
НОД(35,x) = 7.
Тогда искомое второе число x тоже должно делиться на 7, но не делится на 35 его наибольший из существующих делителей. Конечно, таких чисел много (например, то же число 7). Но нам по условию требуется наибольшее из таких чисел, меньшее 35. Очевидно, это число 28.
Ответ: 28.
Слайд 67
Задача 16
Система команд исполнителя РОБОТ, «живущего» в прямоугольном
лабиринте на клетчатой плоскости, состоит из 8 команд. Четыре
команды –
это команды-приказы: вверх, вниз, влево, вправо. При выполнении любой
из этих команд РОБОТ перемещается на одну клетку, соответственно, вверх, вниз, влево или вправо. Четыре других команды проверяют истинность
условия отсутствия стены у каждой стороны той клетки, где находится РОБОТ: сверху свободно, снизу свободно, слева свободно, справа свободно.
Цикл ПОКА условие
последовательность команд
КОНЕЦ ПОКА
выполняется, пока условие истинно.
В конструкции ЕСЛИ условие
ТО команда1
ИНАЧЕ команда2
КОНЕЦ ЕСЛИ
выполняется команда1 (если условие истинно) или команда2 (если условие ложно).
Слайд 68
Задача 16
В конструкциях ПОКА и ЕСЛИ условие может
содержать команды проверки,
а также слова И, ИЛИ, НЕ.
Если
РОБОТ начнет движение в сторону находящейся рядом с ним стены,
то он разрушится и программа прервется.
Сколько клеток лабиринта соответствуют требованию, что, начав движение
в этой клетке и выполнив предложенную программу, РОБОТ уцелеет
и остановится в закрашенной клетке (клетка F6)?
НАЧАЛО
ПОКА снизу свободно ИЛИ справа свободно
ЕСЛИ снизу свободно
ТО вниз
ИНАЧЕ вправо
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ
Слайд 69
Задача 16
Решение
Анализируем предложенную программу РОБОТа.
Слайд 70
Задача 16
Решение
Когда начинается очередной проход цикла, проверяется наличие
стенки снизу. Если ее нет, то выполняется перемещение на
1 клетку вниз. Если же стенка снизу есть, то выполняется перемещение на 1 клетку вправо, причем
без проверки наличия стенки справа. Следовательно, все клетки,
в которых есть стенки снизу и есть стенки справа, можно было бы сразу пометить как непригодные (начав движение из них, РОБОТ разобьется).
Но это не требуется: ведь такое условие записано в цикле ПОКА, который контролирует каждый отдельный шаг РОБОТа. (Вот если бы в цикле ПОКА было записано два или больше таких оператора ЕСЛИ, то для второго и т.д. такого оператора пришлось бы это исключение клеток сделать.)
Слайд 71
Задача 16
Решение
После выполнения одного такого хода проход цикла
завершается,
и вновь выполняется проверка его условия. Нетрудно понять,
что в этом случае движение РОБОТа будет следующим:
«идти вниз, пока это возможно (до стенки снизу), а наткнувшись на стенку снизу – пытаться уходить вправо, отыскивая проход вниз в этой стенке».
Слайд 72
Задача 16
Решение
Именно так мы и будем пытаться «трассировать»
движение РОБОТа.
Увидев, куда в итоге придет РОБОТ, помечаем
все пройденные клетки
розовым цветом (если попадаем в «ловушку»), или зеленым (если доходим
до клетки F6). Сама клетка F6 нам тоже подходит: если РОБОТ изначально находится в ней, то он просто никуда не пойдет.
Остается подсчитать количество клеточек, закрашенных зеленым: их 12.
Ответ: 12.
Слайд 73
Задача 17
У исполнителя Аккорд две команды, которым присвоены
номера:
1. отними 1
2. умножь на
x
(x – неизвестное положительное число).
Выполняя первую из них, Аккорд отнимает от числа на экране 1, а выполняя вторую, умножает это число на x.
Программа для исполнителя Аккорд – это последовательность номеров команд.
Известно, что программа 12121 переводит число 4 в число 23.
Определите значение x.
Слайд 74
Задача 17
Решение
1) Попробуем расписать предложенную программу для исполнителя
Аккорд,
подставляя пока во второй команде значения
x и заполнив левую колонку
заданными исходным и конечным числами:
Слайд 75
Задача 17
Решение
2) Очевидно, что для первой команды можно
сразу записать результат
ее выполнения. Точно так
же можно определить число, которое было
перед выполнением последней команды:
Слайд 76
Задача 17
Решение
3) Вместо оставшихся числовых значений запишем соответствующие
математические выражения и определим, какое математическое выражение
должно давать известное нам предпоследнее число:
x(3x – 1) -1=23
Слайд 77
Задача 17
Решение
4) Тем самым мы получили «ключевое» уравнение,
позволяющее вычислить x:
x(3x – 1) = 24.
Решаем его как обычное квадратное уравнение:
3x2 – x – 24 = 0;
D = 1 + 4324 = 289 = 172;
x1,2 = (117)/(23), тогда x1 = 18/6 = 3, x2 = -16/6 = -8/3.
Поскольку указано, что x – это положительное число, нам подходит только значение 3.
Ответ: 3.
Слайд 78
Задача 18
Ниже приведен фрагмент программы.
При каком наименьшем
введенном числе a после выполнения программы значение переменной c
будет равно 60?
readln(a);
b:=50;
a:=a*2-b;
if a c:=b-10
else
c:=b+10;
Слайд 79
Задача 18
Решение
Требуется проанализировать алгоритм работы программы и понять,
какими могут быть значения введенного числа a.
1) Цикла
нет, и изменение значения переменной b выполняется однократно
(одним из операторов в ветвях then или else).
2) Изначально b = 50, а нам нужно, чтобы это значение стало равным 60.
Следовательно, нужно выполнить оператор c:=b+10 в ветви else.
3) Чтобы выполнялась ветвь else, требуется, чтобы к моменту выполнения
оператора if уже пересчитанное значение a (a:=a*2-b) было не меньше
(т.е. больше или равно) b, т.е. числа 50.
4) Решаем полученное неравенство: a2 – 50 50; 2a 100; a 50.
5) Нужно определить, какое возможное значение a является наименьшим.
Так как неравенство нестрогое, это значение a = 50.
Ответ: 50.
Слайд 80
Задача 19
Сколько существует различных символьных последовательностей длины 5
в трехбуквенном алфавите {К, О, Т}, которые содержат ровно
две буквы О?
Решение
Задача подобна бывшим когда-то заданиям, в которых требовалось определить, какое слово стоит на указанном месте в списке слов, «синтезированных» из букв и отсортированных по порядку, например:
ААААА
ААААО
АААОА
АААОО
ААОАА
…
Такие задачи мы решали, «переводя» буквы в цифры соответствующей системы счисления и работая с полученными числами. Здесь задача несколько иная, но принцип решения будет аналогичен.
Слайд 81
Задача 19
Решение
1) Поскольку никаких слов изначально не задано,
мы можем сами «назначить»
цифры, соответствующие каждой
букве. А поскольку букв в алфавите три,
мы имеем дело с троичной системой счисления и выберем следующие
соответствия букв и цифр:
О – 0, К – 1, Т – 2.
Почему мы выбрали нуль именно для буквы О?
Потому, что нам понадобится искать слова, содержащие ровно две буквы О,
а с нулями это, возможно, окажется проще.
2) Итак, речь идет об определении количества пятиразрядных троичных чисел
(причем незначащие нули слева важны!), содержащих ровно два нуля.
Слайд 82
Задача 19
Решение
3) Первый нуль может быть в одной
из 5 позиций – получаем 5 вариантов.
Как
в каждом из этих вариантов может располагаться второй нуль?
Когда первый нуль находится в позиции «1», второй нуль может
располагаться в одной из 4 оставшихся позиций – «2», «3», «4», «5».
Когда первый нуль находится в позиции «2», второй нуль может
располагаться в одной из 3 оставшихся позиций правее – «3», «4» и «5»
(ведь ситуацию, когда нули располагаются в позициях «1» и «2», мы уже
рассмотрели перед этим);
когда первый нуль находится в позиции «3», второй нуль может
располагаться в одной из 2 оставшихся позиций правее – «4» и «5»
(почему, – рассмотрено выше);
когда первый нуль находится в позиции «4», второй нуль может
располагаться только в 1 позиции правее – «5».
Итого получаем 4 + 3 + 2 + 1 = 10 вариантов размещения в пятиразрядном
числе двух нулей.
Слайд 83
Задача 19
Решение
Возможны другие рассуждения, приводящие к тому же
результату.
Условно обозначим наши нули разными цветами: например, первый –
синим,
а второй – красным.
Тогда синий нуль можно разместить в пяти разрядах – получаем 5 вариантов.
В каждом из этих пяти вариантов красный нуль можно разместить в любой
из оставшихся четырех позиций – т.е. по четырем вариантам. Значит, всего получаем 54 = 20 вариантов размещения разноцветных нулей.
А теперь вспомним, что на самом деле оба нуля (синий и красный) – совершенно равноправны. Значит, пары «синий – красный» и «красный – синий» (если читать число слева направо) – это одни и те же пары. Следовательно, каждая такая пара посчитана дважды, и всего вариантов размещения в пятиразрядном числе двух одинаковых нулей будет 10.
Слайд 84
Задача 19
Решение
Итак, существует 10 вариантов размещения в числе
двух нулей.
В каждом из этих 10 вариантов остается
три цифры, которые могут быть равны или 1, или 2.
Сколько может быть таких неповторяющихся комбинаций?
Очевидно, столько, сколько может быть различных трехразрядных чисел
в системе счисления, состоящей из двух цифр (т.е. двоичной).
Значит, для каждого из 10 ранее найденных вариантов получается
23 = 8 «подвариантов».
Тогда общее число троичных чисел, в которых из пяти цифр ровно две – нулевые, будет равно 810 = 80.
Ответ: 80.
Слайд 85
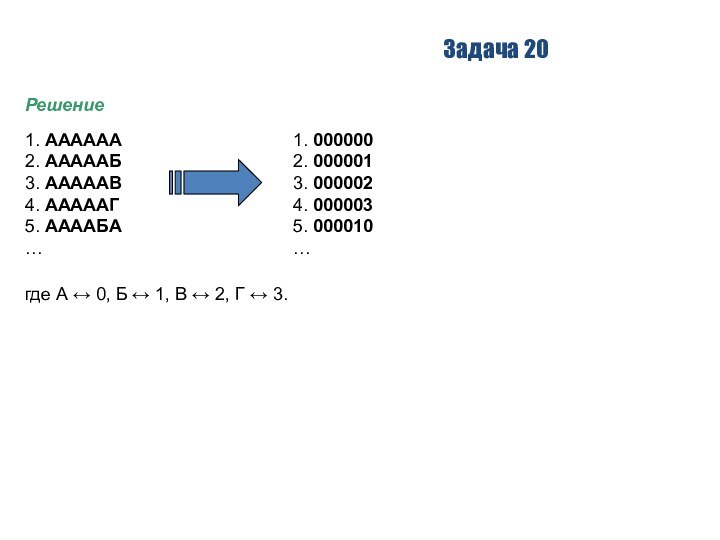
Задача 20
Все 6-буквенные слова, составленные из букв А,
Б, В и Г, записаны
в алфавитном порядке и
пронумерованы. Вот начало такого списка:
1. АААААА
2. АААААБ
3. АААААВ
4. АААААГ
5. ААААБА
…
Под каким номером в этом списке располагается первое слово, начинающееся с буквы Г?
Слайд 86
Задача 20
Решение
1. АААААА
2. АААААБ
3. АААААВ
4. АААААГ
5. ААААБА
…
1. 000000
2.
000001
3. 000002
4. 000003
5. 000010
…
где А ↔ 0, Б ↔
1, В ↔ 2, Г ↔ 3.
Слайд 87
Задача 20
Решение
1) Какое первое по возрастанию шестизначное четверичное
число
будет начинаться с тройки (с аналога буквы Г)?
Очевидно, 3000004.
2) В приведенном списке под номером 1 идет число 0000004, т.е. 010,
под номером 2 – число 0000014, т.е. 110 и т.д. Значит, номер в списке
искомого числа 3000004 (первого слова, начинающегося с Г),
надо преобразовать его в десятичную систему счисления
и к полученному десятичному числу прибавить 1:
3000004 = 3 45 = 307210;
3072 + 1 = 3073.
Ответ: 3073.
Слайд 88
Задача 21
Ниже приведена программа.
При каком наибольшем введенном
числе d после выполнения программы
будет напечатано 55?
var n, s, d: integer;
begin
readln(d);
n := 0;
s := 0;
while s <= 365 do
begin
s := s + d;
n := n + 5;
end;
write(n);
end.
Слайд 89
Задача 21
Решение
1) Анализируем алгоритм:
в цикле ПОКА задано
условие выполнения цикла – до тех пор, пока значение
s не превышает 365;
внутри цикла значение переменной s увеличивается на заданное значение
d, а значение переменной n увеличивается на 5;
по завершении цикла на экран выводится значение переменной n.
2) Тогда, согласно условию, значение n равно 55. Учитывая, что изначально
переменная n обнуляется, это означает, что цикл выполнился 55/5 = 11 раз.
Слайд 90
Задача 21
Решение
3) Учитывая, что переменная s изначально тоже
обнуляется, получаем,
что за эти 11 проходов
цикла переменная s увеличивается на 11d
и становится больше 365 (условие прекращения работы цикла).
Тогда получаем неравенство:
11d > 365,
откуда d > 365/11, т.е. d > 33 2/11, или, учитывая, что числа – целые, d >= 34.
4) Чтобы теперь оценить верхнюю границу интервала возможных значений d,
надо учесть, что при слишком большом значении d цикл мог бы прерваться
еще после 10 проходов (а то и раньше). Значит, нам нужно определить
значение d, на единицу меньшее, чем минимальное значение d,
обеспечивающее выполнение 10 проходов цикла.
В этом случае неравенство будет таким:
10d > 365,
тогда d > 365/10, или d > 36,5.
Слайд 91
Задача 21
Решение
5) Рассуждая аналогично п. 3, можно заключить,
что минимальное значение d,
при котором цикл
завершится через 10 проходов, равно 37 (ближайшее
целое число, большее 36,5). Нам же требуется значение d, на единицу
меньшее. Это – число 36.
Таким образом, диапазон возможных значений d, обеспечивающих выполнение 11 проходов цикла, составляет [34 .. 36], а искомое максимальное значение d, при котором будет выведено число 55, равно 36.
Ответ: 36.
Слайд 92
Задача 22
Алгоритм вычисления значения функции F(n), где n
– натуральное число,
задан следующими соотношениями:
F(n) =
1 при n2;
F(n) = F(n – 2)(n + 2) при n>1.
Чему равно значение функции F(8)?
Решение
Это – задача на рекурсию. В условии этого задания отметим ошибку, делающую это условие внутренне противоречивым:
вторая строка, определяющая соотношения для функции F(n),
должна иметь вид: F(n) = F(n – 2)(n + 2) при n>2.
Слайд 93
Задача 22
Решение
Само решение заключается в аккуратном расписывании всех
значений F(n) для возрастающих значений n от 1 до
требуемого значения 8, при этом
для вычисления очередного значения используются ранее вычисленные предыдущие значения F(n):
F(1) = 1;
F(2) = 1;
F(3) = F(3 – 2)(3 + 2) = F(1)5 = 15 = 5;
F(4) = F(4 – 2)(4 + 2) = F(2)6 = 16 = 6;
F(5) = F(5 – 2)(5 + 2) = F(3)7 = 57 = 35;
F(6) = F(6 – 2)(6 + 2) = F(4)8 = 68 = 48;
F(7) = F(7 – 2)(7 + 2) = F(5)9 = 359 = 315;
F(8) = F(8 – 2)(8 + 2) = F(6)10 = 4810 = 480.
Последнее вычисленное значение – и есть искомый ответ.
Ответ: 480.
Слайд 94
Задача 23
Алгоритм вычисления значения функции F(n), где n
– натуральное число, задан следующими соотношениями:
F(1) = 3; F(2)
= 3;
F(n) = 8*F(n–1) – 7*F(n–2) при n > 2.
Чему равно значение функции F(2014)?
Слайд 95
Задача 23
Решение
На первый взгляд кажется, что на решение
этой задачки придется потратить чуть ли не всю свою
жизнь.
Но так ли это сложно на самом деле? Проверим!
F(3) = 8*F(3–1) – 7*F(3–2) = 8*F(2) –7*F(1) = 8*3 – 7*3 = 3;
F(4) = 8*F(4–1) – 7*F(4–2) = 8*F(3) –7*F(2) = 8*3 – 7*3 = 3; …
Можно легко догадаться, что формула для вычисления очередного члена последовательности составлена так, что при одинаковых значениях
F(1) и F(2) по этой формуле всегда будет получаться число 3.
Значит, задача очень-очень простая. И ответ к ней можно дать сразу же:
это (независимо от того, про F от какого n в ней спрашивается)
всегда будет число 3.
Ответ: 3.
Слайд 96
Задача 24
Известно, что для целого числа x выполнено:
334+x – 334 = 3310.
Определите значение x. Ответ запишите в десятичной системе счисления.
Слайд 97
Задача 24
Решение
1) Запишем «каноническое» преобразование обоих недесятичных чисел
в десятичную систему счисления (согласно формуле вида
a1a0n = a1n1 + a0n0):
334+x = 3(4 + x)1 + 3(4 + x)0 = 3(4 + x) + 3 = 12 + 3x + 3 = 15 + 3x;
334 = 341 + 340 = 34 + 3 = 15.
2) Теперь, когда все числа переведены в десятичную систему счисления,
можно записать уравнение в виде:
15 + 3x – 15 = 33,
откуда 3x = 33, тогда x = 11.
Ответ: 11.
Слайд 98
Задача 25
Записан алгоритм. Получив на вход число x,
этот алгоритм печатает два числа: a и b. Сколько
существует таких чисел x, при вводе которых алгоритм печатает сначала 2, а потом 15?
var x, a, b: integer;
begin
readln(x);
a:=0; b:=0;
while x>0 do
begin
a := a + 1;
b := b + (x mod 10);
x := x div 10;
end;
writeln(a); writeln(b);
end.
Слайд 99
Задача 25
Решение
1) Как всегда, начинаем с анализа алгоритма:
цикл ПОКА выполняется до тех пор, пока x не
станет нулем;
в цикле значение переменной a каждый раз увеличивается на 1,
следовательно, a – это счетчик количества проходов цикла;
переменная b служит доля накапливания суммы значений x mod 10, а затем
переменная x (исходное число) переприсваивается на значение x div 10.
Такой алгоритм – это разбор в цикле исходного числа x на отдельные цифры
(справа налево), а в переменной b вычисляется сумма цифр исходного числа;
после цикла выводится сначала значение переменной a,
а затем – переменной b.
Слайд 100
Задача 25
Решение
2) По условию, в ходе выполнения алгоритма
были выведены числа 2 и 15, –
значит, a = 2, а b = 15. Следовательно, цикл выполнился 2 раза
(а значит, в исходном числе x было 2 цифры), а сумма цифр
этого числа равна 15.
3) Для ответа на вопрос задачи нужно определить, сколько существует
двузначных натуральных чисел, сумма цифр которых равна 15.
Их нетрудно найти простым перебором (учитывая и то, что суммы цифр
могут быть и «симметричными»). Для этого по очереди предполагаем
первую цифру равной 1, 2, 3 и т.д. и определяем, чему может быть равна
вторая цифра:
69, 96, 78, 87.
Всего – 4 числа.
Ответ: 4.
Слайд 101
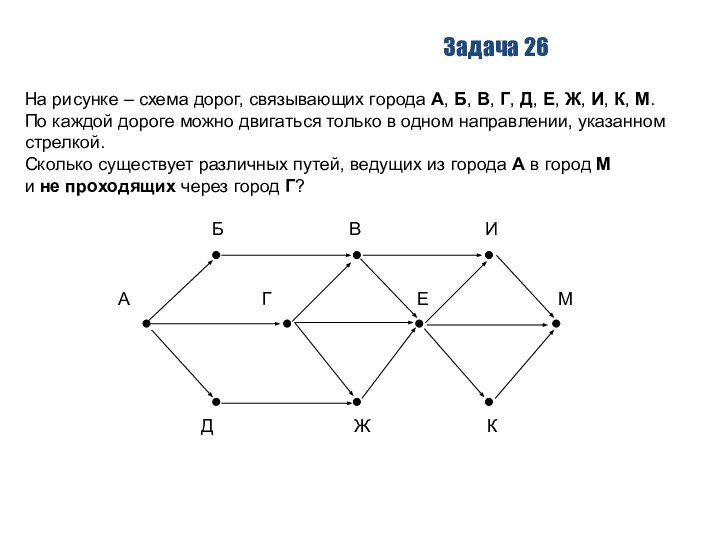
Задача 26
На рисунке – схема дорог, связывающих города
А, Б, В, Г, Д, Е, Ж, И, К,
М.
По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.
Сколько существует различных путей, ведущих из города А в город М
и не проходящих через город Г?
Слайд 102
Задача 27
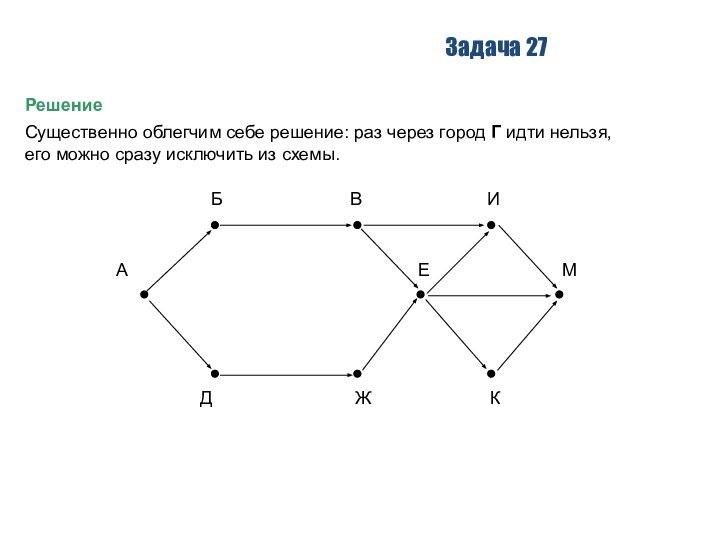
Решение
Существенно облегчим себе решение: раз через город
Г идти нельзя,
его можно сразу исключить из схемы.
Слайд 103
Задача 27
Решение
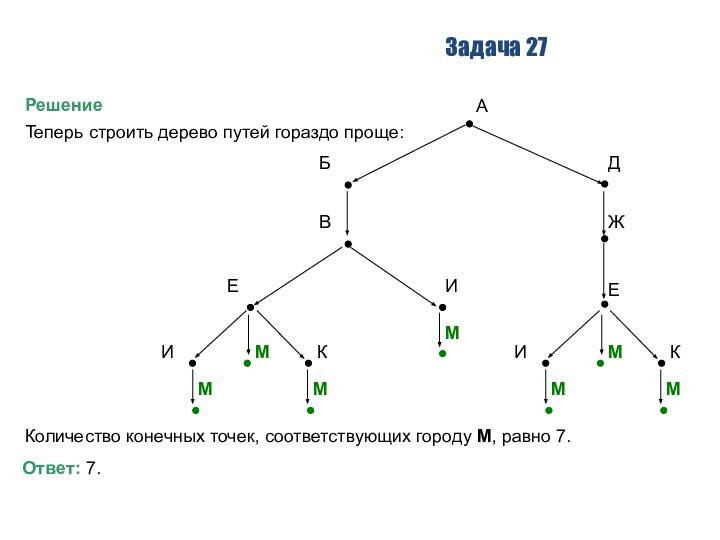
Теперь строить дерево путей гораздо проще:
Количество конечных
точек, соответствующих городу М, равно 7.
Ответ: 7.
Слайд 104
Задача 28
Данные объемом 80 Мбайт передаются из пункта
А в пункт Б по каналу связи, обеспечивающему скорость
передачи данных 223 бит в секунду, а затем
из пункта Б в пункт В по каналу связи, обеспечивающему скорость передачи данных 220 бит в секунду. От начала передачи данных из пункта А
до их полного получения в пункте В прошло 13 минут.
Через какое время в секундах началась передача данных в пункте Б,
т.е. каково время между началом передачи данных из пункта А
и началом передачи данных в пункт В?
В ответе укажите только число, слово «секунд» или букву «с» добавлять
не нужно.
Слайд 105
Задача 28
Решение
1) Построим диаграмму Ганта для этой задачи:
При
этом следует учитывать, что процесс передачи данных из Б
в В
по условию задачи начинается уже после того, как завершится передача данных из А в Б.
Слайд 106
Задача 28
Решение
2) Составляем по этой схеме уравнение (t
– это время задержки
между окончанием приема
данных из А и началом их передачи в В).
Для этого вычисляем время передачи данных из А в Б и из Б в В:
из А в Б: 80 (Мбайт) / 223 (бит в секунду) = 5227 (бит) / 223 (бит в секунду) =
= 524 = 80 (с);
из Б в В: 80 (Мбайт) / 220 (бит в секунду) = 5227 (бит) / 220 (бит в секунду) =
= 527 = 640 (с).
Записываем уравнение:
80 + t + 640 = 13 (минут) = 1360 (с), т.е. 720 + t = 780, откуда t = 60.
3) Чтобы найти время от начала передачи данных из А в Б до начала
их передачи из Б в В, нужно к найденному значению t прибавить время
передачи данных из А в Б: 80 + 60 = 140 (с).
Ответ: 140.
Слайд 107
Задача 29
В терминологии сетей TCP/IP маской сети называется
двоичное число, определяющее, какая часть IP-адреса узла сети относится
к адресу сети,
а какая – к адресу самого узла в этой сети. Обычно маска записывается
по тем же правилам, что и IP-адрес – в виде четырех байтов, причем каждый байт записывается в виде десятичного числа. При этом в маске сначала
(в старших разрядах) стоят единицы, а затем с некоторого места – нули.
Адрес сети получается в результате применения поразрядной конъюнкции
к заданному IP-адресу узла и маске.
Например, если IP-адрес узла равен 231.32.255.131, а маска равна 255.255.240.0, то адрес подсети равен 231.32.240.0.
Для узла с IP-адресом 224.128.112.142 адрес сети равен 224.128.64.0.
Чему равен третий слева байт маски?
Ответ запишите в виде десятичного числа.
Слайд 108
Задача 29
Решение
1) Преобразуем заданные третьи слева байты исходного
IP-адреса
и адреса сети в двоичные числа:
11210 = 11100002;
6410 = 10000002.
2) Для получения из исходного IP-адреса заданного адреса сети требовалась
поразрядная конъюнкция (для каждого бита) IP-адреса и маски, т.е.:
Биты маски нам неизвестны. Но их очень легко определить:
там, где значения битов IP-адреса и адреса сети оба равны 1,
бит маски должен быть тоже равен 1;
там, где бит IP-адреса равен 1, а бит адреса сети равен 0,
бит маски должен быть равен 0.
Слайд 109
Задача 29
Решение
Единственная неоднозначность – там, где биты IP-адреса
и адреса сети
оба равны нулю: тут бит маски
может быть равен как 0, так и 1. Но устранить
эту неоднозначность нетрудно, зная, что в маске при ее просмотре слева направо может быть только один переход от единичных битов к нулевым,
т.е., например, маска 11000110 недопустима. А мы видим, что уже со второго слева бита в маске должны начаться нули. Значит, и во всех «спорных» битах маски правее этого места тоже должны быть только нули.
3) Теперь нетрудно восстановить вышеприведенный «ребус» с конъюнкцией
двоичных чисел:
4) Остается перевести найденную двоичную маску в десятичное число.
Для этого даже не понадобится никаких вычислений – полученная маска
полностью совпала с двоичной записью байта адреса сети (19210), значит,
и искомый байт маски тоже равен 192
Слайд 110
Задача 30
В языке запросов поискового сервера для обозначения
логической операции «ИЛИ» используется символ «|», а для логической
операции «И» – символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
Какое количество страниц (в тысячах) будет найдено по запросу США?
Считается, что все запросы выполнялись практически одновременно,
так что набор страниц, содержащих все искомые слова, не изменялся
за время выполнения запросов.
Слайд 111
Задача 30
Решение
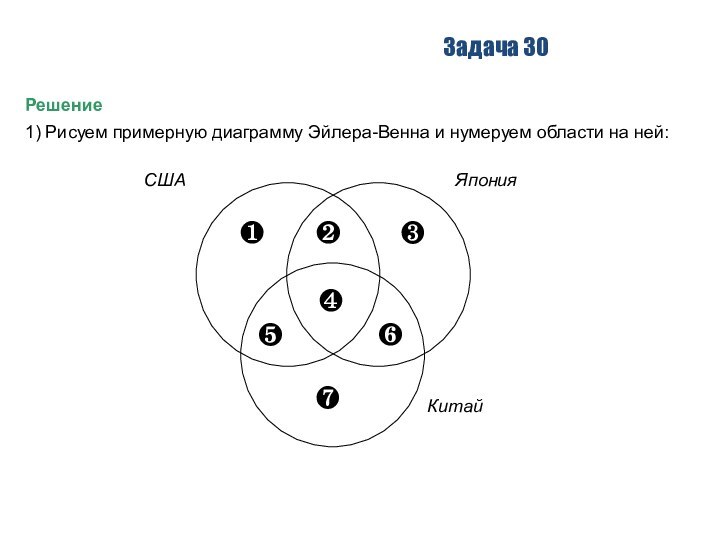
1) Рисуем примерную диаграмму Эйлера-Венна и нумеруем
области на ней:
Слайд 112
Задача 30
Решение
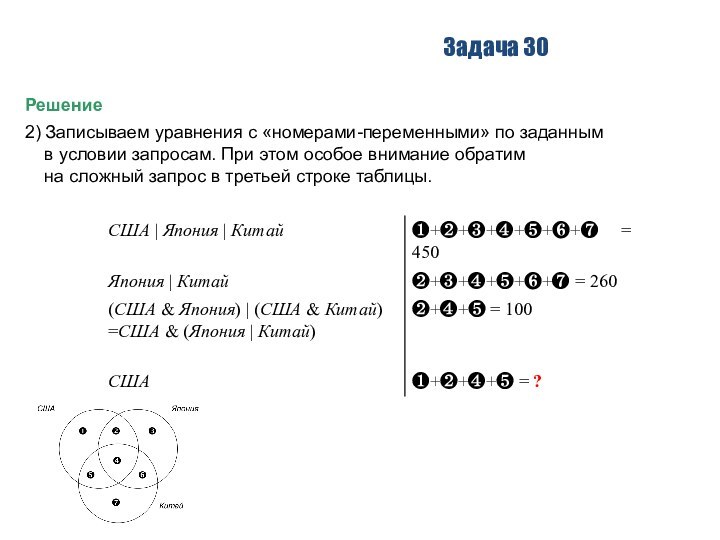
2) Записываем уравнения с «номерами-переменными» по заданным
в условии запросам. При этом особое внимание
обратим
на сложный запрос в третьей строке таблицы.
Слайд 113
Задача 30
Решение
3) Теперь главное – найти, как удобнее
всего решить эту систему уравнений.
Но это
неожиданно легко.
Сразу очевидно, что из уравнений:
++++++ = 450
и
+++++ = 260
можно найти значение , равное 450 – 260 = 190.
Тогда зная, что ++ = 100,
сразу можно вычислить, что +++ = 190 + 100 = 290.
Ответ: 290.
Слайд 114
Задача 31
Элементами множества А являются натуральные числа. Известно,
что выражение
(x ∈ {2, 4, 6, 8, 10,
12}) → (((x ∈ {3, 6, 9, 12, 15}) /\ ¬(x ∈ A)) → ¬(x ∈ {2, 4, 6, 8, 10, 12}))
истинно (т. е. принимает значение 1) при любом значении переменной х. Определите наименьшее возможное значение суммы элементов множества A.
Слайд 115
Задача 31
Обозначим B={2k|k=1,2,…,6}, C={3m|m=1,2,…5}. Тогда представленное выражение запишется
(x
in B) -> (((x in C) and not (x
in A)) -> not ( x in B)), или
B-> ((C and not A) -> not B).
Упростим полученное выражение (используются определение импликации и законы двойственности),
B->(not (C and notA) or not B)
not B or (not C or A or not B)
not B or not C or A or not B
получим A or not B or not C, или A or not (B and C). И это выражение должно быть всегда истинно.
Пусть x не принадлежит множеству A, тогда из условия истинности x принадлежит дополнению множества B∩C. Значит, A содержится в этом множестве.
Найдем пересечение множеств B∩C={6;12}. Если A не содержит хотя бы один из указанных элементов, например, число 6, то при этом x условие истинности выражения нарушается. Значит A=B∩C.
Далее сумма элементов A легко считается. Ответ: 18
Слайд 116
Задача 32
Определите, какое значение Н нужно ввести, чтобы
число, напечатанное
в результате выполнения следующего алгоритма, было наименьшим.
var a,b,t,M,R,H : integer;
Function F(H, x: integer):integer;
begin
F := 11*(x-H)*(x-H)+13;
end;
begin
readln(H);
a:=-10; b:=50;
M:=a; R:=F(H,a);
for t:=a to b do begin
if (F(H,t)>R then begin
M:=t;
R:=F(H,t);
end;
end;
write(R);
end.
Слайд 117
Задача 32
Решение
Это несколько усложненное задание типа В14 (с
параболами). Такие задачи встречались ранее, но тогда требовалось для
функции одной переменной F(x), представляющей собой квадратное уравнение, найти, какое число выводится
в результате. А теперь имеется функция с двумя переменными F(H,x), которая представляет собой квадратное уравнение с параметром H, и искать надо значение этого параметра, такое, чтобы выводимое значение
было наименьшим.
Прежде всего, заметим, что работа в языке программирования с функциями
с одной и с двумя переменными полностью идентична: в обоих случаях
в функцию передаются значения переменных, а результат возвращается
через саму функцию F(). Поэтому сосредоточимся на собственно решении.
Слайд 118
Задача 32
Решение
1) Анализируем алгоритм.
В цикле идет
перебор значений t от заданных ранее a = –10
до b = 50.
При этом в переменной M запоминается сначала начальное значение a,
а потом (при срабатывании условного оператора) – текущее значение t,
а в переменной R хранится предыдущее значение функции F(H,x).
Если с увеличением значения t получаемое значение F() увеличивается
(и в результате оказывается больше предыдущего значения F(t),
запомненного в переменной R), то текущее значение t заносится
в переменную M, а значение функции в этой точке запоминается в R.
До каких пор это будет продолжаться? Посмотрим на выражение,
записанное в составе функции F(). Выполним в нем перемножение скобок.
Получим:
11*(x-H)*(x-H)+13 = 11x2 – 22xH + (11H2 +13).
Слайд 119
Задача 32
Решение
Это – запись квадратного уравнения (если приравнять
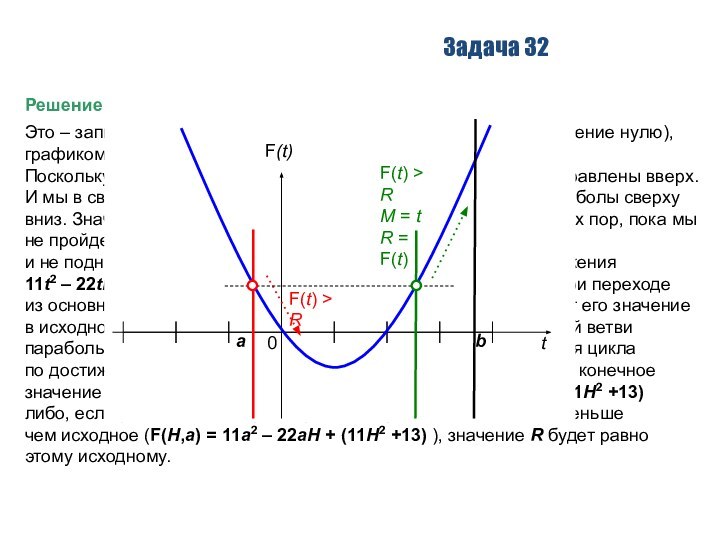
это выражение нулю), графиком которого является парабола.
Поскольку перед
x2 стоит знак «плюс», ветви этой параболы направлены вверх. И мы в своих вычислениях «движемся» по левой ветви этой параболы сверху вниз. Значит, условный оператор в цикле не будет работать до тех пор, пока мы не пройдем вершину параболы (минимум на ее графике)
и не поднимемся по правой ветви настолько, что значение выражения
11t2 – 22tH + (11H2 +13) (замена переменной x на t происходит при переходе
из основной программы в функцию) в некоторой точке t превысит его значение в исходной точке a. А после этого, пока мы «движемся» по правой ветви параболы вверх, значение R будет всё расти вплоть до окончания цикла
по достижении точки b (см. примерный рисунок). Следовательно, конечное значение R равно значению выражения F(H,b) = 11b2 – 22bH + (11H2 +13)
либо, если расположить параболу так, что указанное значение меньше
чем исходное (F(H,a) = 11a2 – 22aH + (11H2 +13) ), значение R будет равно этому исходному.
Слайд 120
Задача 32
Решение
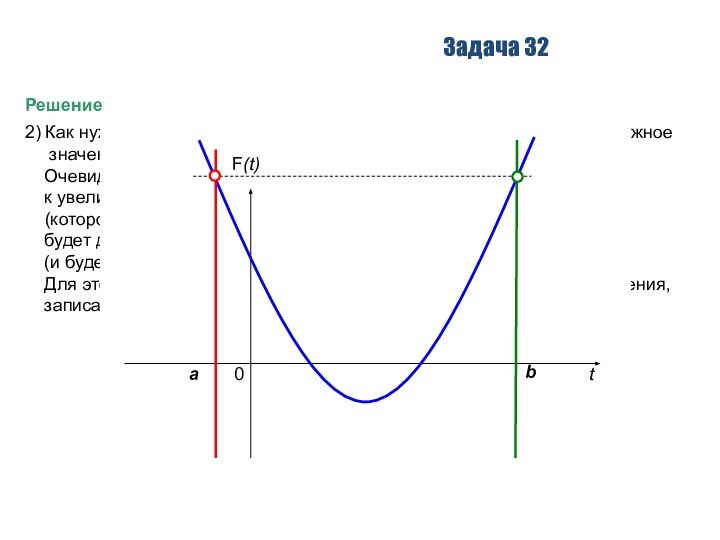
2) Как нужно расположить параболу, чтобы получить
минимально возможное
значение R? И каким
оно будет?
Очевидно, что если ветвь then начнет работать, то это приведет
к увеличению значения R. Следовательно, наименьшее значение R
(которое и выводится на экран в результате работы программы),
будет достигаться, если ветвь then так ни разу и не сработает
(и будет равным значению в исходной точке a).
Для этого требуется, чтобы в точках a = –10 и b = 50 значения выражения,
записанного в функции, были равными.
Слайд 121
Задача 32
Решение
3) Остается вычислить значение H такое, чтобы
получить нужное
расположение параболы. Для этого
надо составить уравнение в виде:
11a2 – 22aH + (11H2 +13) = 11b2 – 22bH + (11H2 +13)
или, подставляя известные нам значения a = –10 и b = 50:
11(-10)2 – 22(-10)H + (11H2 +13) = 11502 – 2250H + (11H2 +13).
Очевидно, одинаковые слагаемые (11H2 +13) сразу сокращаются.
Также можно разделить обе его части на 11.
Получаем уравнение первого порядка:
(-10)2 – 2(-10)H = 502 – 250H.
Решаем его:
100 + 20H = 2500 – 100H; 100 + 20H = 2500 – 100H;
120H = 2400; H = 20.
Ответ: 20.
Слайд 122
var a,b,t,m,r,h:integer;
function f(H,x:integer):integer;
begin
f:=(x-30)*(x-H);
end;
begin
readln(H);
a:=10;b:=80;
m:=a;R:=f(h,a);
for t:=a to b do begin
if
(f(h,t)
нужно ввести, чтобы число, напечатанное в результате выполнения следующего алгоритма, было наименьшим. Если таких значений несколько, то в ответе запишите максимальное из них.
Слайд 123
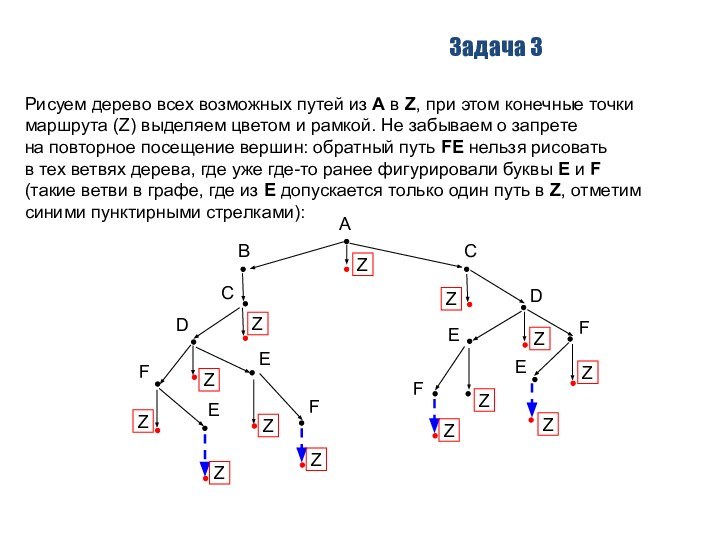
Программа находит минимум среди значений функции f в
точках интервала [10 ; 80] с целочисленными абсциссами (или
первый минимум, если их несколько) и выводит абсциссу этого минимума m.
Очевидно, что наименьшее возможное значение m равно 10 (левая граница интервала). Функция f представляет собой параболу с корнями 30 и Н (ветви вверх). Поскольку вершина параболы находится точно в середине между корнями, мы можем найти ее абсциссу (30+Н)/2 .
Слайд 124
Минимум (первый минимум) может оказаться в точке 10
в двух случаях - если значения функции на интервале
монотонно возрастают или если они равны друг другу в двух первых точках (10 и 11), а далее монотонно возрастают (в квадратичной параболе ординаты могут быть равными не более, чем у двух точек). Первому случаю соответствует бесконечно много значений Н, при которых вершина лежит не правее левой границы данного интервала, второму случаю – единственное значение Н, при котором вершина находится между первой и второй точками, т.е. имеет абсциссу 10,5 . Этот случай нас и интересует, т.к. соответствует максимальному значению Н. Получаем уравнение (30+Н)/2 = 10,5 , откуда Н=-9.



























![123 Задача 11На числовой прямой даны да отрезка: P = [43, 49] и](/img/tmb/11/1041459/6dedb01fb06aaee90d663f24395b3ff4-720x.jpg)



![123 Задача 12На числовой прямой даны два отрезка: X = [7,11] и Y](/img/tmb/11/1041459/3d2feebca06fe9059056c7a874343d86-720x.jpg)

![123 Задача 12Решение (способ 1)1) Z = [8,10] «Неизменные» отрезки: [–,7], [7,8], [8,9],](/img/tmb/11/1041459/818bb360705a61ff9b0104b9de9aab7a-720x.jpg)
![123 Задача 12Решение (способ 1)1) Z = [8,10] Логическое выражение:Есть отрезки, где](/img/tmb/11/1041459/38cd67c860a0020253440160509fd4ca-720x.jpg)
![123 Задача 12Решение (способ 1)2) Z = [6,12]«Неизменные» отрезки: [–,6], [6,7], [7,9], [9,11],](/img/tmb/11/1041459/5b5260bd23c40268955886a1cc0e266d-720x.jpg)
![123 Задача 12Решение (способ 1)2) Z = [6,12]Логическое выражение:Есть отрезки, где логическое выражение обращается в нуль!](/img/tmb/11/1041459/3273d13e2a90c592730584aed6c2693c-720x.jpg)
![123 Задача 12Решение (способ 1)3) Z = [6,14]«Неизменные» отрезки: [–,6], [6,7], [7,9], [9,11],](/img/tmb/11/1041459/cf9e89bbf19a6f6eac391b2df3a24f66-720x.jpg)
![123 Задача 12Решение (способ 1)3) Z = [6,14]Логическое выражение:Логическое выражение везде равно единице](/img/tmb/11/1041459/44376ca7d0599620b011b1cc2aff068a-720x.jpg)
![123 Задача 12Решение (способ 1)4) Z = [8,18]«Неизменные» отрезки: [–,7], [7,8], [8,9], [9,11],](/img/tmb/11/1041459/993aa441eb91a8aedb95645bc2654afe-720x.jpg)
![123 Задача 12Решение (способ 1)4) Z = [8,18]Логическое выражение:Есть отрезки, где логическое выражение обращается в нуль!](/img/tmb/11/1041459/f45ef7f92c69729a93d3ae3a63e801bc-720x.jpg)



![123 Задача 12Решение (способ 2)1) Z = [8,10] По крайней мере, интервалы [7,8]](/img/tmb/11/1041459/828ca55c97e77cd1ac5082eb19b2d158-720x.jpg)
![123 6. Игра с отрезками Решение (способ 2)2) Z = [6,12]Второе правило нарушено](/img/tmb/11/1041459/0b72ceb395c72cb6d5e1efffb9d1959b-720x.jpg)
![123 6. Игра с отрезками Решение (способ 2)3) Z = [6,14]Нарушений правил нигде](/img/tmb/11/1041459/e1e35e4b5e8d2010774752245ff28d1f-720x.jpg)
![123 6. Игра с отрезками Решение (способ 2)4) Z = [8,18]Первое правило нарушено](/img/tmb/11/1041459/f8c3a3d37ecf03fd3500b6e528c4de64-720x.jpg)