Слайд 2
"Мысль выражать все числа десятью знаками, придавая им
кроме значения по форме еще значение по месту, настолько
проста, что именно из-за этой простоты трудно понять, насколько она удивительна."
П.Лаплас
Слайд 3
Она в 101 класс ходила. В портфеле по
100 книг носила.
Всё это правда, а не бред.
Когда пыля
десятком ног , Она шагала по дороге,
За ней всегда бежал щенок
С одним хвостом, зато стоногий,
Она ловила каждый звук своими десятью ушами,
И десять загорелых рук Портфель и поводок держали.
И десять темно-синих глаз
Оглядывали мир привычно.
Но станет все совсем обычным ,
Когда поймете наш рассказ.
Слайд 5
Древнеегипетская нумерация
1. Как и большинство людей для счета
небольшого количества предметов Египтяне использовали палочки.
Если палочек нужно
изобразить несколько, то их изображали в два ряда, причем в нижнем должно быть столько же палочек сколько и в верхнем, или на одну больше.
Слайд 6
10. Такими путами египтяне связывали коров
Если нужно
изобразить несколько десятков, то иероглиф повторяли нужное количество раз.
Тоже самое относится и к остальным иероглифам.
100. Это мерная веревка, которой измеряли земельные участки после разлива Нила.
Слайд 7
Древнегреческая нумерация
1, 2, 3, 4
6, 7, 8,
9
10
Слайд 10
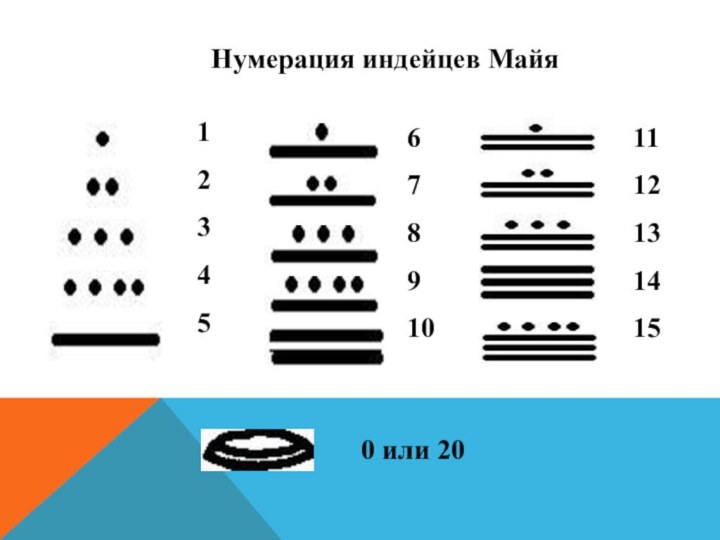
Нумерация индейцев Майя
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
0 или 20
Слайд 11
Китайская нумерация
°
1
2
3
4
5
6
7
8
9
0
10
100
1000
Слайд 12
Славянская кириллическая нумерация
Слайд 14
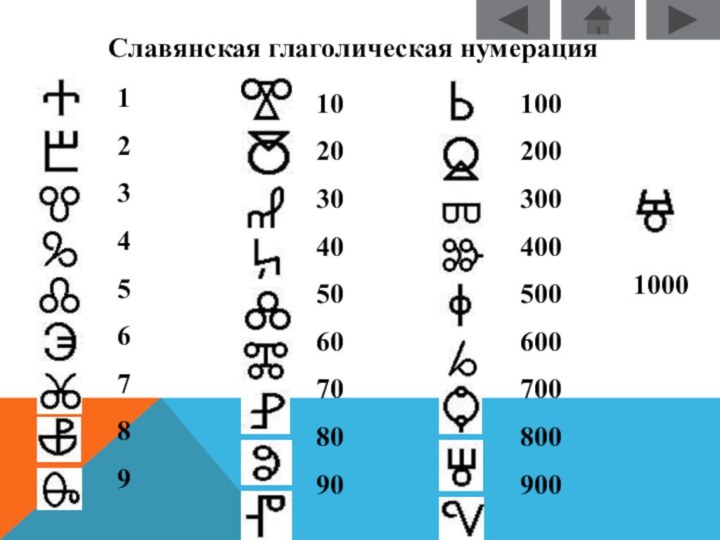
Славянская глаголическая нумерация
1
2
3
4
5
6
7
8
9
10
20
30
40
50
60
70
80
90
100
200
300
400
500
600
700
800
900
1000
Слайд 16
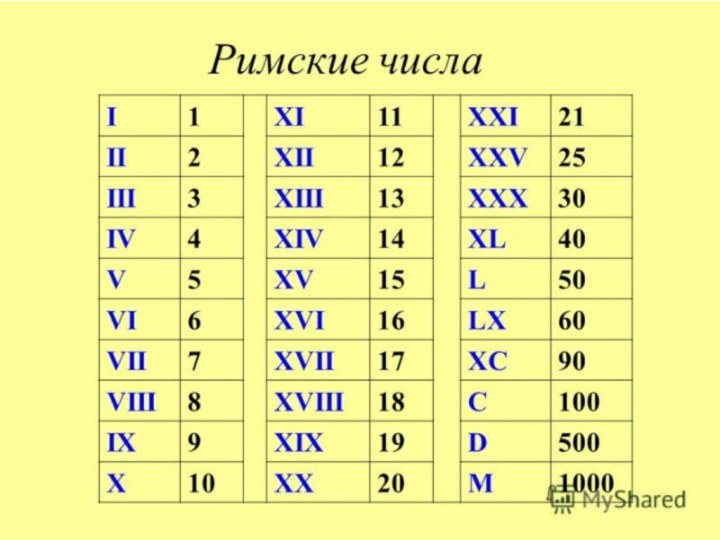
ПРИМЕНЕНИЕ РИМСКОЙ СС
Принято указывать номер тысячелетия или века
римскими символами.
Используется при написании "порядкового номера" монаршей особы.
Номера
томов в многотомном литературном произведении. Иногда таким образом нумеруются разделы или главы книг.
Римские цифры используют для обозначения важных исторических событий или пунктов перечня. Помимо тем, так или иначе связанных с историей, данную систему счисления используют в химии и медицине.
Петр I
Слайд 17
АРАБСКАЯ СИСТЕМА СЧИСЛЕНИЯ
Это, самая распространенная на сегодняшний день
нумерация. Применяемые в настоящее время цифры 1234567890 сложились в
Индии около 400 г. н.э. Арабы стали пользоваться подобной нумерацией около 800 г.н.э.,а примерно в 1200 г.н.э. ее начали применять в Европе, однако в Европе они стали известны благодаря трудам арабских математиков, и потому за ними утвердилось название «арабские», хотя сами арабы вплоть до настоящего времени пользуются совсем другими символами.
Арабские числа:
Слайд 18
Арабская система-десятичная, с основанием 10 и с использованием
десяти цифр, которыми можно выразить все возможные числа. Арабская
система счисления является позиционной
Из арабского языка заимствовано и слово «цифра» (по-арабски «сыфр»), означающее буквально «пустое место». Та форма, которой мы сейчас пользуемся, установилась в XVI веке.
Слайд 19
Арабская системы счисления
Впервые такая система, вернее ее зачатки
появилась в Древнем Вавилоне, почти в то же время
она была изобретена в Китае, потом в Индии, откуда перекочевала на Аравийский полуостров, а затем и в Европу. Здесь эту систему счисления назвали Арабской, и под этим именем она разошлась по всему миру. Так что, говоря "арабские числа" надо иметь в виду, ну, хотя бы индийские.
Слайд 20
Не из учебника задача,
А потрудней открылся шифр.
Ребята
поняли, что значат
Простые с виду десять цифр.
Да, путь
познания не гладок,
Но знайте вы со школьных лет:
Загадок больше, чем разгадок,
И поискам предела нет!
Слайд 21
Пятеричная СС…
В сказке "Конёк-Горбунок", написанной П. П. Ершовым,
есть примечательный эпизод. Царь, увидев златогривых коней и пожелав
их заполучить, вступает с Иваном в торг.
Ну, я пару покупаю.
Продаешь, ты? — Нет, меняю.
Что в промен берешь добра? —
Два — пять шапок серебра. —
То есть это будет десять.
Царь тотчас велел отвесить...
Слайд 22
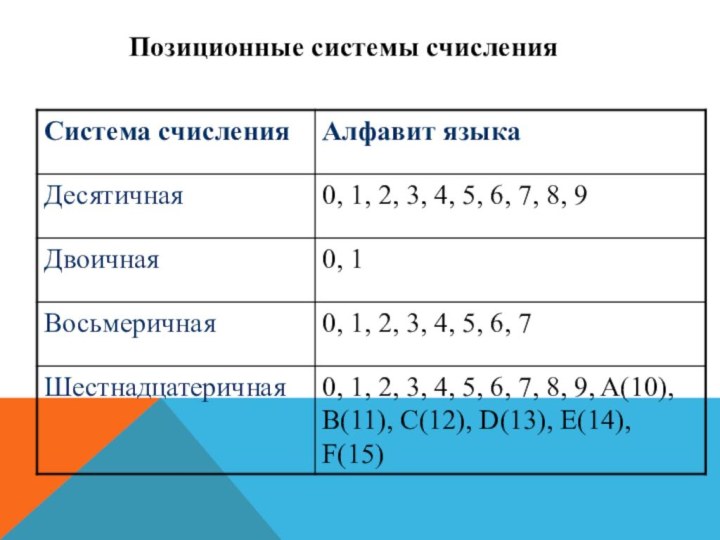
Системы счисления
позиционные
Непозиционные
Слайд 24
75 10 = 2
371 8 = 10
1100110101011 2
= 8
1100110101011 2 = 16
110 5
201 5 115 5 10111 5 61 5
Слайд 25
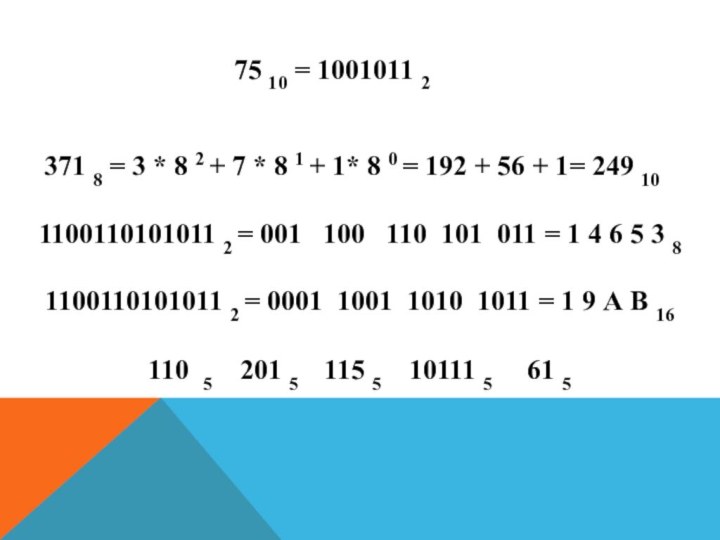
75 10 = 1001011 2
371 8 = 3
* 8 2 + 7 * 8 1 +
1* 8 0 = 192 + 56 + 1= 249 10
1100110101011 2 = 001 100 110 101 011 = 1 4 6 5 3 8
1100110101011 2 = 0001 1001 1010 1011 = 1 9 А В 16
110 5 201 5 115 5 10111 5 61 5
Слайд 26
Переведите десятичные дробные числа в двоичную систему счисления.
1
команда - 0,25 и 0,3 (с точностью 4 знака)
2 команда -
0,75 и 0,4 (с точностью 4 знака)
Ответы:
0,2510 = 0,012
0,7510 = 0,112
0,310 = 0,01002
0,410 = 0,01102
Слайд 32
В комнате веселились 1425 мух. Иван Иванович открыл
форточку и размахивая полотенцем, выгнал из комнаты 225 мух.
Но прежде, чем он успел закрыть форточку, 213 мух вернулись обратно. Сколько мух теперь веселится в комнате?
Сколько дырок окажется в клеенке, если во время обеда 1011 раз проткнули ее вилкой с 111 зубчиками.
Преступники решили порвать со своим прошлым и начать новую трудовую жизнь. Для этого они украли 11002 лопат, 112 молотков 1002 отверток. Сколько всего орудий честного труда украли преступники.
Слайд 33
2: 10112*1112=10011012
3: 11002+112+1002=11112= 1510
1:
2 1 0
1425=1*52+4*51+2*50=4710
1 0
225=2*51+2*50=1210
1 0
213=2*31+1*30=710
4710-1210+710=4210
Слайд 34
Упорядочить числа по убыванию
50 9, 1222 5, 1011
4, 110011 2, 125 8
Ответ: 12225, 1258, 10114,
1100112, 509
Слайд 35
Найдите среднее арифметическое следующих чисел:
1 команда
2 команда
2258,5F16,548
9816,
3Е16, 10101012
Ответ: 9610
Ответ: 10010
Слайд 36
Практическая работа
«Подбери соответствие»
с использованием программы
Калькулятор
Пуск-Программы-Стандартные-Калькулятор
Режимы
калькулятора: обычный и инженерный
Вид-инженерный
Hex- шестнадцатеричная система
Dec- десятичная система
Oct- восьмиричная
система
Bin- двоичная система
Слайд 38
1 - Урок полезен, все понятно
2 - Лишь
кое-что чуть-чуть неясно
3 - Еще придется потрудиться
4 - Да,
трудно все-таки учиться
Слайд 39
Домашнее задание.
1. Выпишите целые числа принадлежащие промежутку: [3616;
4016]
2. Существует ли треугольник, длины сторон которого выражаются числами
128,1116,110112?
3. Вычислите выражение
1228+101112*1012
4. Чему равно х в десятичной системе счисления, если:
х=107+102*105
5. Переведите числа из десятичной системы счисления в двоичную: 100,45 99 0,8125
6. Переведите число в десятичную систему счисления: 110 000, 1112
Слайд 40
Дополнительное задание.
Переведите в двоичную систему счисления.
200410
и 300410
Ответы:
200410 = 11 111 010 1002
300410 = 101
110 111 1002







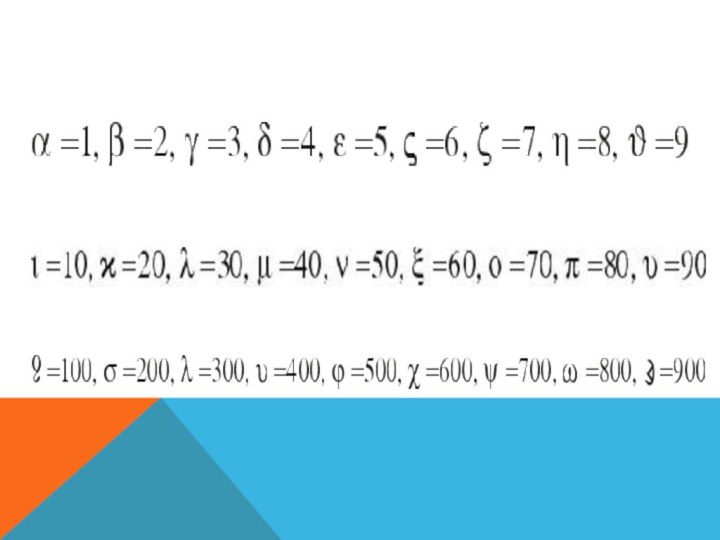























![Презентация к открытому уроку по информатике в 10 классе на тему Системы счисления Домашнее задание.1. Выпишите целые числа принадлежащие промежутку: [3616; 4016]2. Существует ли треугольник,](/img/tmb/6/524221/dd154de485c00d6d05bf1d6aa4cdecc6-720x.jpg)

