- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по информатике на тему Системы счисления
Содержание
- 2. Древний ЕгипетДревний Вавилон"Всё есть число"Арабские цифры
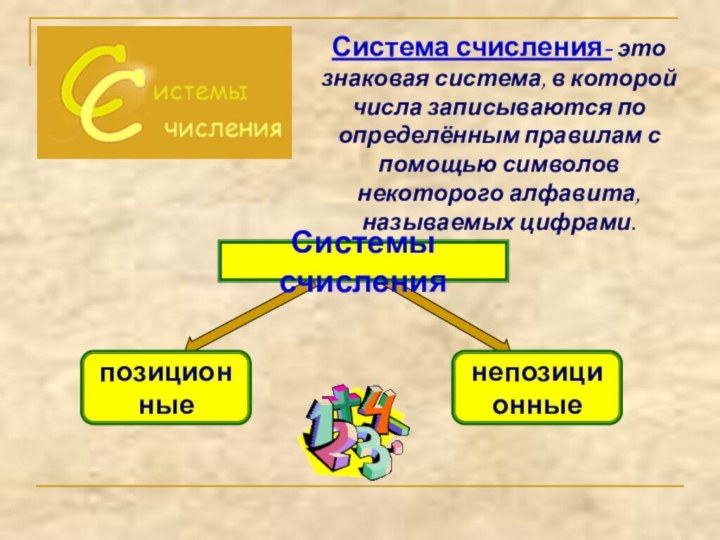
- 3. Система счисления- это знаковая система, в которой
- 4. I – 1; V- 5; X- 10;L-
- 5. I – 1V- 5X- 10L- 50C- 100D-
- 6. Основанием системы может быть любое
- 7. Позиционные системы счисления
- 8. Развёрнутая форма записи числаПример 2:
- 9. Связь систем счислений
- 10. Перевод чисел из десятичной СС в другие
- 11. Скачать презентацию
- 12. Похожие презентации
Древний ЕгипетДревний Вавилон"Всё есть число"Арабские цифры









Слайд 4
I – 1; V- 5; X- 10;
L- 50;
C- 100;
D- 500; M- 1000
Непозиционные системы счисления
Древнеегипетская десятичная СС
Единичная
(унарная) ССАлфавитная СС
Римская СС
Как считали греки
I – 1; Г- 5; Δ- 10;
H- 100; X- 1000;
M- 10000
Слайд 5
I – 1
V- 5
X- 10
L- 50
C- 100
D- 500
M-
1000
Непозиционная римская СС
Каждый символ обозначает всегда одно и
тоже число;Например:
XXX – 30;
XLI – 41;
МСМLXXXVII -1987
Слайд 6
Основанием системы может быть любое
натуральное число, большее единицы;
Значение цифры зависит от ее
позиции, т.е. одна и та же цифра соответствует разным значениям в
зависимости от того, в какой позиции числа она стоит;
Например: 888: 800; 80; 8
Позиционные системы счисления
Слайд 8
Развёрнутая форма записи числа
Пример 2:
11012
= 1·2³+1·2²+0·2¹+1·2º=8+4+0+1=1310
Пример 1:
253910 = 2·10³+5·10²+3·10¹+9·10ºПример 3:
4135 = 4·5²+1·5¹+3·5º=100+5+3=10810
Слайд 10
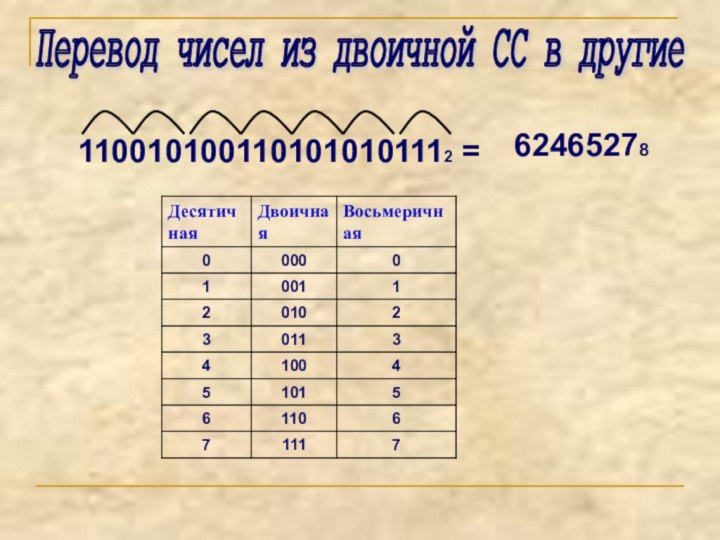
Перевод чисел из десятичной СС в другие
Разделить
десятичное число на основание. Получится частное и остаток.
Частное
опять разделить на основание. Получится частное и остаток.Выполнять деление до тех пор, пока последнее частное не станет меньшим основания.
Записать последнее частное и все остатки в обратном порядке. Полученное число и будет записью исходного десятичного числа в нужной СС.