- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по информатике на тему Логические основы работы компьютера
Содержание
- 2. В основе современной логики лежат учения, созданные
- 3. Логика – это наука о формах и способах мышления. Это учение о способах рассуждений и доказательств.
- 4. Законы мира, сущность предметов, общее в них
- 5. Понятие – это форма мышления, которая выделяет
- 6. Высказывание – это формулировка своего понимания окружающего
- 7. По поводу высказывания можно сказать, истинно оно
- 8. Упражнение (устно)Какие из предложений являются высказываниями? Определите
- 9. Умозаключение позволяет на основе известных фактов, выраженных
- 10. Логические выражения и операцииАлгебра – это наука
- 11. Логические выражения и операцииЛогическая переменная – это
- 12. Логические выражения и операцииСоставное высказывание – логическая
- 13. Логические выражения и операцииЛогические операции – логическое
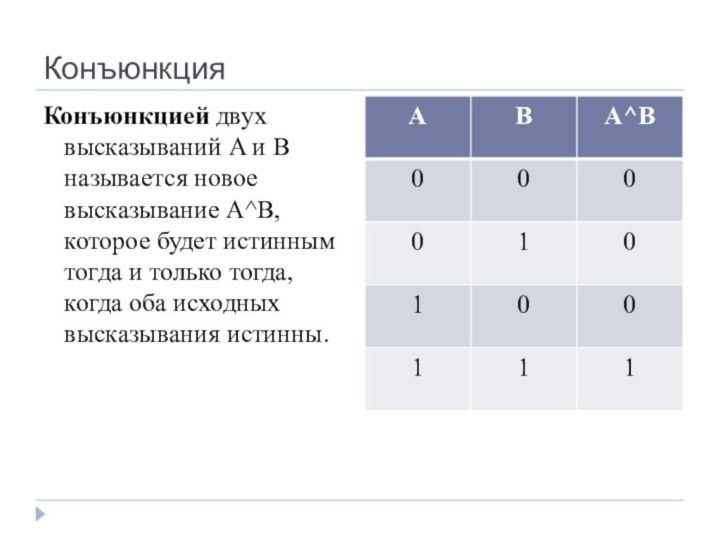
- 14. КонъюнкцияКонъюнкцией двух высказываний A и B называется
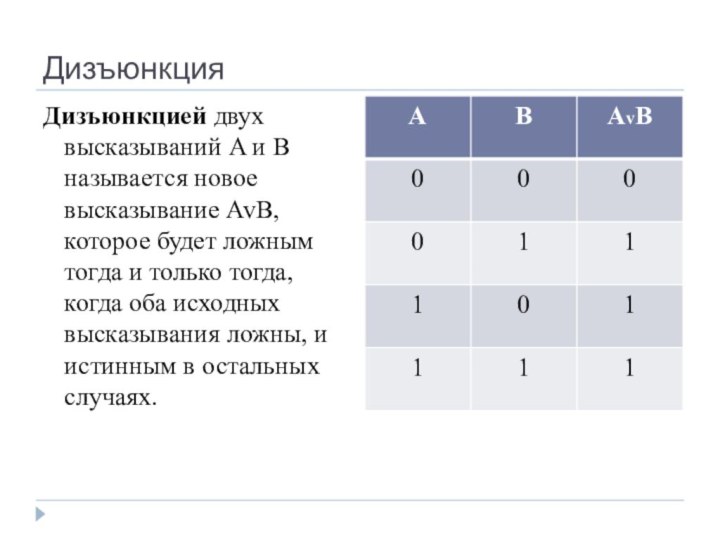
- 15. ДизъюнкцияДизъюнкцией двух высказываний A и B называется
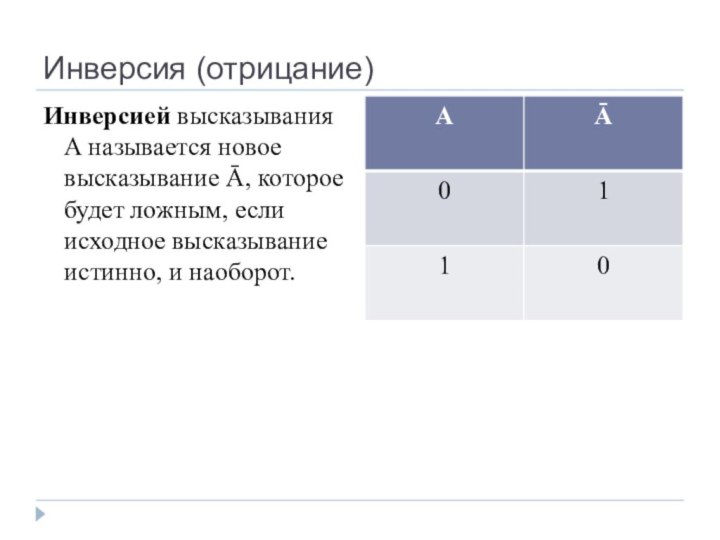
- 16. Инверсия (отрицание)Инверсией высказывания A называется новое высказывание
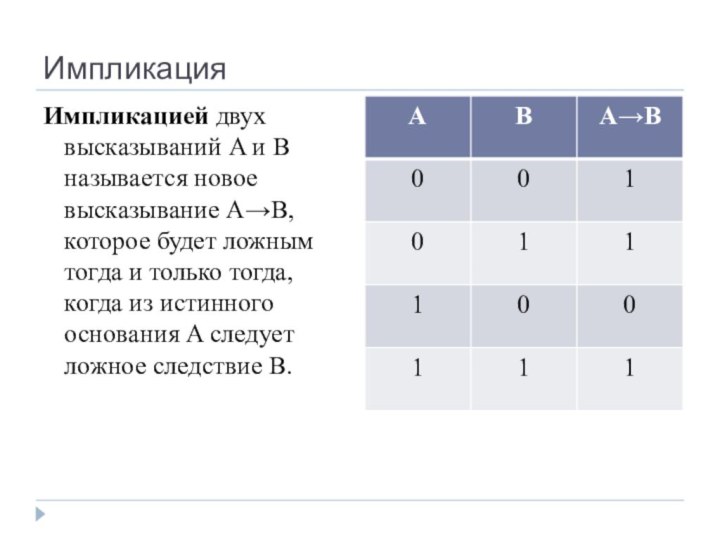
- 17. ИмпликацияИмпликацией двух высказываний A и B называется
- 18. Скачать презентацию
- 19. Похожие презентации
В основе современной логики лежат учения, созданные еще древнегреческими мыслителями, хотя первые учения о формах и способах мышления возникли в Древнем Китае и Индии. Основоположником формальной логики является Аристотель, который впервые отделил логические формы мышления от













Слайд 3
Логика – это наука о формах и способах
мышления. Это учение о способах рассуждений и доказательств.
Слайд 4
Законы мира, сущность предметов, общее в них мы
познаем посредством абстрактного мышления. Логика позволяет строить формальные модели
окружающего мира, отвлекаясь от содержательной стороны.Мышление всегда осуществляется через понятия, высказывания и умозаключения.
Слайд 5
Понятие – это форма мышления, которая выделяет существенные
признаки предмета или класса предметов, позволяющие отличать их от
других.Пример
Прямоугольник, проливной дождь, компьютер.
Слайд 6
Высказывание – это формулировка своего понимания окружающего мира.
Высказывание является повествовательным предложением, в котором
что-либо утверждается или отрицается.
Слайд 7
По поводу высказывания можно сказать, истинно оно или
ложно. Истинным будет высказывание, в котором связь понятий правильно
отражает свойства и отношения реальных вещей. Ложным высказывание будет в том случае, когда оно противоречит реальной действительности.Пример
«Буква «а» – гласная».
«Компьютер был изобретен в середине XIX века».
Слайд 8
Упражнение (устно)
Какие из предложений являются высказываниями? Определите их
истинность.
1. Какой длины эта лента?
2. Прослушайте сообщение.
3. Делайте утреннюю
зарядку!4. Кто отсутствует?
5. Париж – столица Англии.
6. Число 11 является простым.
7. Сложите числа 2 и 5.
8. Некоторые медведи живут на севере.
9. Все медведи – бурые.
Слайд 9
Умозаключение позволяет на основе известных фактов, выраженных в
форме суждений, получать новое знание.
Умозаключение – это форма мышления,
с помощью которой из одного или нескольких суждений может быть получено новое суждение (знание или вывод).
Слайд 10
Логические выражения и операции
Алгебра – это наука об
общих операциях, аналогичных сложению и умножению, которые выполняются не
только над числами, но и над другими математическими объектами, в том числе и над высказываниями. Такая алгебра называется алгеброй логики. Алгебра логики отвлекается от смысловой содержательности высказываний и принимает во внимание только истинность или ложность высказывания.
Слайд 11
Логические выражения и операции
Логическая переменная – это простое
высказывание, содержащее только одну мысль. Ее символическое обозначение –
латинская буква (например, A, B, C и т.д.). Значением логической переменной могут быть только константы ИСТИНА и ЛОЖЬ (1 и 0).
Слайд 12
Логические выражения и операции
Составное высказывание – логическая функция,
которая содержит несколько простых мыслей, соединенных между собой с
помощью логических операций. Ее символическое обозначение – F(A,B,…).На основании простых высказываний могут быть построены составные высказывания.