Слайд 2
Современный человек в повседневной жизни постоянно сталкивается с
числами: мы запоминаем номера автобусов и телефонов, в магазине
подсчитываем стоимость покупок, ведём свой семейный бюджет в рублях и копейках (сотых долях рубля) и т.д. Числа, цифры... они с нами везде. А что знал человек о числах несколько тысяч лет назад? Вопрос непростой, но очень интересный. Историки доказали, что и пять тысяч лет назад люди могли записывать числа и производить над ними арифметические действия. Конечно, принципы записи были совсем не такими, как сейчас. Но в любом случае число изображалось с помощью одного или нескольких символов.
Эти символы, участвующие в записи числа, в математике и информатике принять называть цифрами
Слайд 3
Но что же люди понимают тогда под словом
"число"?
Слайд 4
Первоначально понятие отвлечённого числа отсутствовало, число было "привязано"
к тем конкретным предметам, которые пересчитывали. Отвлечённое понятие натурального
числа появляется вместе с развитием письменности. Дробные же числа изобрели тогда, когда возникла необходимость производить измерения. Измерение, как известно, это сравнение с другой величиной того же рода, выбираемой в качестве эталона.
Эталон называется ещё единицей измерения. Понятно, что единица измерения не всегда укладывалась целое число раз в измеряемой величине. Отсюда и возникла практическая потребность ввести более "мелкие" числа, чем натуральные. Дальнейшее развитие понятия числа было обусловлено уже развитием математики.
Понятие числа - фундаментальное понятие как математики, так и информатики. В дальнейшем при изложении материала под числом мы будем понимать его величину, а не его символьную запись.
Слайд 5
Система счисления - это способ записи (изображения) чисел.
Сегодня, в
самом конце XX века, для записи чисел человечество использует
в основном десятичную систему счисления. А что такое система счисления?
Слайд 6
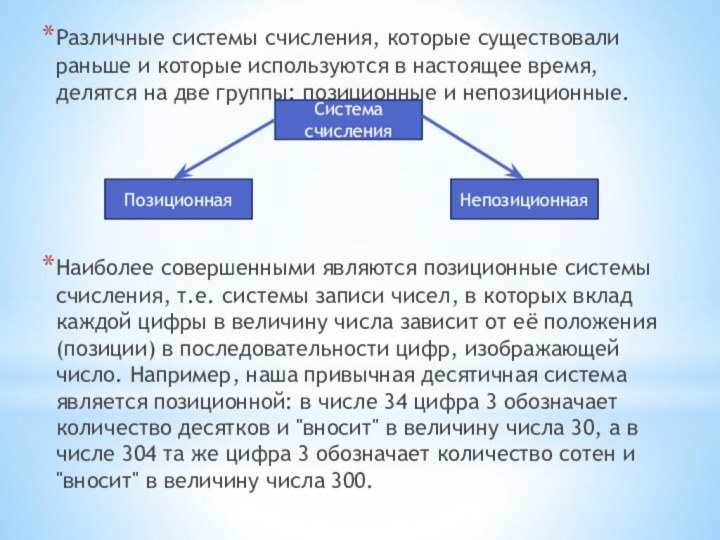
Различные системы счисления, которые существовали раньше и которые
используются в настоящее время, делятся на две группы: позиционные
и непозиционные.
Наиболее совершенными являются позиционные системы счисления, т.е. системы записи чисел, в которых вклад каждой цифры в величину числа зависит от её положения (позиции) в последовательности цифр, изображающей число. Например, наша привычная десятичная система является позиционной: в числе 34 цифра 3 обозначает количество десятков и "вносит" в величину числа 30, а в числе 304 та же цифра 3 обозначает количество сотен и "вносит" в величину числа 300.
Система счисления
Позиционная
Непозиционная
Слайд 7
Единичная система
Потребность в записи чисел появилась в очень

древние времена, как только люди начали считать. Количество предметов,
например овец, изображалось нанесением чёрточек или засечек на какой - либо твёрдой поверхности: камне, глине, дереве (до изобретения бумаги было ещё очень и очень далеко). Каждой овце в такой записи соответствовала одна чёрточка. Археологами найдены такие "записи" при раскопках культурных слоёв, относящихся к периоду палеолита (10 - 11 тысяч лет до н.э.).
Учёные назвали этот способ записи чисел единичной ("палочной") системой счисления. В ней для записи чисел применялся только один вид знаков - "палочка". Каждое число в такой системе счисления обозначалось с помощью строки, составленной из палочек, количество которых и равнялось обозначаемому числу.
Неудобства такой системы записи чисел и ограниченность её применения очевидны: чем большее число надо записать, тем длиннее строка из палочек. Да и при записи большого числа легко ошибиться, нанеся лишнее количество палочек или, наоборот, не дописав их.
Можно предложить, что для облегчения счёта люди стали группировать предметы по 3, 5, 10 штук. И при записи использовали знаки, соответствующие группе из нескольких предметов. Естественно, что при подсчёте использовались пальцы рук, поэтому первыми появились знаки для обозначения группа предметов из 5 и 10 штук (единиц). Таким образом, возникли уже более удобные системы записи чисел.
Слайд 9
Вспомните где?
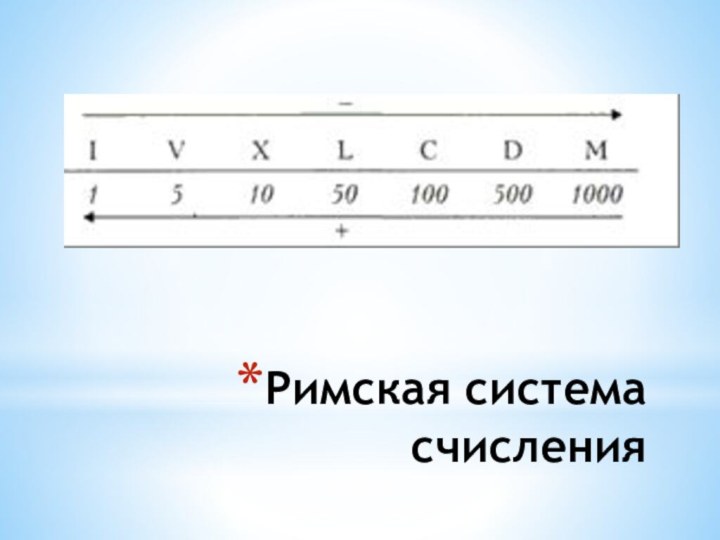
Самой распространенной из непозиционных систем счисления является
римская система.
Главная проблема с римскими цифрами заключается в том,
что сложно производить умножение и деление. Другим недостатком римской системы является: Запись больших чисел требует введения новых символов. А дробные числа можно записывать только как отношение двух чисел. Тем не менее, они были основными до конца средних веков. Но и в наше время их ещё используют.
Слайд 10
Значение цифры не зависит от ее положения в
числе.
Например, в числе XXX (30) цифра X встречается трижды
и в каждом случае обозначает одну и ту же величину - число 10, три числа по 10 в сумме дают 30.
Слайд 11
Величина числа в римской системе счисления определяется как
сумма или разность цифр в числе.
Если меньшая цифра стоит
слева от большей, то она вычитается, если справа - прибавляется.