Слайд 2
Раздел 19. Оптимизация конструкций с учетом динамики
ЧТО ТАКОЕ

“ОПТИМИЗАЦИЯ КОНСТРУКЦИЙ”?………..………………………………………………..……… 19 - 4
ОСОБЕННОСТИ ОПТИМИЗАЦИИ С ПОМОЩЬЮ MSC.Nastran………………………………………...………
19 - 5
ПРЕИМУЩЕСТВА ОПТИМИЗАЦИИ КОНСТРУКЦИЙ С ПОМОЩЬЮ MSC.Nastran……………….……….. 19 - 6
ВОЗМОЖНОСТИ ОПТИМИЗАЦИИ С ПОМОЩЬЮ MSC.Nastran ……………………………………………… 19 - 7
ПОСТАНОВКА ЗАДАЧИ ОПТИМИЗАЦИИ……………………………………………………………….………….. 19 - 9
ОПТИМИЗАЦИИ КОНСТРУКЦИЙ В MSC.Nastran ……………..…………………………………………………. 19 - 10
ОБЫЧНО ИСПОЛЬЗУКМЫЕ ОПЕРАТИРЫ BULK DATA…….………………………………………….……… 19 - 12
ПРИМЕР №15 – ОПТИМИЗАЦИЯ С УЧЕТОМ СОБСТВЕННЫХ КОЛЕБАНИЙ….………………..…………. 19 - 13
ОПЕРАТОРЫ ОПТИМИЗАЦИИ...……………………………………………………………………...………… 19 - 15
ВХОДНОЙ ФАЙЛ ДЛЯ ПРИМЕРА №15..…………………………………………………………….………… 19 - 16
РЕЗУЛЬТАТЫ РЕШЕНИЯ ПРИМЕРА №15…..…….……………………………………...…………………… 19 - 18
ПРЯМОЕ ЗАДАНИЕ ШИРОКОИСПОЛЬЗУЕМЫХ ФУНКЦИЙ…………………………………………………… 19 - 23
ПРИМЕР ОПТИМИЗАЦИИ С ИСПОЛЬЗОВАНИЕМ ЧАСТОТНОГО ОТКЛИКА.………………………….…. 19 - 24
ОПЕРАТОРЫ ОПТИМИЗАЦИИ…...………………………………………………………………………..…….. 19 - 25
ЗАДАНИЕ ДИНАМИЧЕСКИХ НАГРУЗОК………...………………………………………………………...…… 19 - 26
ОПЕРАТОР TABLED4 ДЛЯ ЭТОГО ПРИМЕРА……………………………………………………...…………. 19 - 27
“ЧУВСТВИТЕЛЬНОСТЬ” ДИНАМИЧЕСКОГО ОТКЛИКА..……………………………………………..………. 19 - 28
ОПИСАНИЕ “КОНСТРУКТОРСКОЙ” МОДЕЛИ….……………………………………………………………….. 19 - 29
ВХОДНОЙ ФАЙЛ ДЛЯ ОПТИМИЗАЦИОННОЙ МОДЕЛИ…………………………………………………...…… 19 - 30
ФРАГМЕНТ ФАЙЛА CAR.BLK……………………………………………………………………………………….. 19 - 31
ФРАГМЕНТ ФАЙЛА SPRINGS.BLK…………….……………………………………………………………...…… 19 - 32
ФРАГМЕНТ ФАЙЛА OPTIM.BLK ……………………………………………………………………………...…… 19 - 33
Слайд 3
Оптимизация конструкций с учетом динамики (продолж.)
ПРИМЕР №16 –
ОПТИМИЗАЦИЯ С ИСПОЛЬЗОВАНИЕМ ЧАСТОТНОГО ОТКЛИКА…………………… 19 -
35
РЕШЕНИЕ ДЛЯ УПРАЖНЕНИЯ 16…..…………………………………………………………………………….. 19 – 36
РЕЗУЛЬТАТЫ РЕШЕНИЯ ЗАДАЧИ ОПТИМИЗАЦИИ.…………………………………………………..…….. 19 - 42
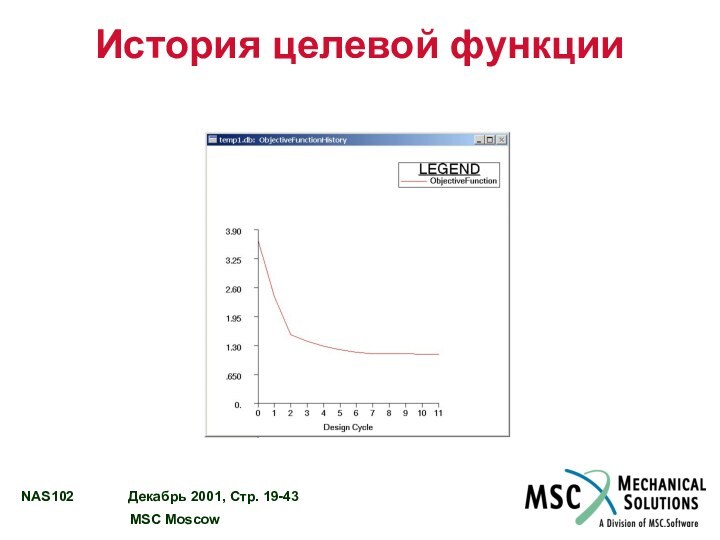
ИСТОРИЯ ЦЕЛЕВОЙ ФУНКЦИИ………………………………………………………………………………… 19 - 43
ИСТОРИЯ ПЕРЕМЕННЫХ ПРОЕКТИРОВАНИЯ.…….……………………………………………………… 19 - 44
ПЕРЕМЕЩЕНИЕ КОЛЕСА ….…………………………………………………………………………………… 19 - 45
ПЕРЕМЕЩЕНИЕ СИДЕНЬЯ ВОДИТЕЛЯ …………..………………………………………………………… 19 - 46
ЗАКЛЮЧЕНИЕ………………………………………………….……………………………………………………… 19 - 47
Слайд 4
Что такое “Оптимизация конструкций”?
Автоматическое изменение параметров расчетной модели
для достижения поставленной цели при обеспечении выполнения конструктивных ограничений.
ОБЛАСТИ
ПРИМЕНЕНИЯ
Улучшение конструкции объекта (оптимизация)
Получение физически реализуемой конструкции из нереализуемой
Подбор параметров модели для получения требуемого отклика
Идентификация параметров системы
Анализ корреляции расчетной модели и опытных данных (см. Раздел 20)
Другие (в зависимости от выдумки конструктора)
Слайд 5
Особенности оптимизации с помощью MSC.Nastran
Простота исследования возможности создания
конструкции
Понятие “конструкторской” модели
Гибкость в представлении “конструкторской” модели
Задаваемые пользователем уравнения,
интерпретирующие требования к конструкции
Эффективное решение задач любой размерности
Количество выполняемых КЭ расчетов как мера эффективности
Слайд 6
Преимущества оптимизации конструкций с помощью MSC.Nastran
Высокая эффективность решения
от малых до больших задач
Надежная сходимость решения
Гибкий интерфейс пользователя
(в т.ч. возможность задания пользователем основных уравнений)
Полное использование аппроксимационного подхода
Постоянное улучшение алгоритмов
Результаты базируются на доказанной надежности MSC.Nastran
Высокий уровень поддержки как части MSC.Nastran
Доступ к знакомым инструментам анализа MSC.Nastran
Слайд 7
Возможности оптимизации с помощью MSC.Nastran
Multi-Disciplinary Optimization
Оптимизация с учетом
статического отклика
Оптимизация с учетом устойчивости
Оптимизация с учетом динамических эффектов
Прямой
анализ частотного отклика
Модальный анализ частотного отклика
Модальный анализ переходного процесса
Акустический анализ
Оптимизация с использованием суперэлементов
Границы суперэлементов “прозрачны” для конструкторской модели.
Оптимизация с учетом аэроупругости
Статическая аэроупругость
Флаттер
Слайд 8
Возможности оптимизации с помощью MSC.Nastran
Оптимизация формы
Четыре метода генерации
базовых векторов
“Ручная” вариация положения узлов
Прямой ввод формы
Геометрический граничные формы
Аналитические
граничные формы
Слайд 9
Постановка задачи оптимизации
Переменные проектирования
Цель:
Минимизация F(X)
При соблюдении:
Ограничения типа
“меньше или равно”:
Ограничения типа “равно”:
Двухсторонние ограничения:
Слайд 10
Оптимизация конструкций в MSC.Nastran
Оператор ANALYSIS в Case Control
Section позволяет задать тип анализа, используемого при оптимизации, для
каждого из расчетных случаев (subcase’ов).
С помощью оператора ANALYSIS можно инициализировать следующие типы анализа:
STATICS - статический
MODES - собственных колебаний
BUCK - устойчивости
DFREQ - частотного отклика (прямой)
MFREQ - частотного отклика (модальный)
MTRAN - переходного процесса (модальный)
SAERO - статической аэроупругости
FLUTTER - флаттера
Слайд 11
Оптимизация конструкций в MSC.Nastran
Пример оптимизации с учетом двух
статических расчетов (subcase 1 и subcase 2), расчета частотного
отклика модальным методом (subcase 3) и анализа переходного процесса (subcase 4).
Слайд 12
Обычно используемые операторы Bulk Data
DESVAR - Определяет переменную проектирования.
DVPREL1 -

Задает связь между свойством расчетной модели и переменной
проектирования.
DLINK - Задает связи между одной или несколькими переменными проектирования.
DRESP1 - Непосредственно определяет параметр, используемый либо в качестве
ограничения (для этого он указывается оператором DCONSTR в Bulk Data
Section), либо как целевая функция (инициализируется оператором DESOBJ
в Case Control Section).
DCONSTR - Определяет ограничительную функцию (инициализируется оператором
DESSUB в Case Control Section).
DCONADD - Определяет ограничительную функцию для subcase’а объединением
нескольких операторов DCONSTR.
DRESP2 - Определяет комплексный параметр, используемый либо в качестве
ограничения, либо в качестве целевой функции.
DEQATN - Задает уравнения, используемые при оптимизации.
DVCREL1 - Определяет связь между параметром топологии элемента и переменной
проектирования.
DVCREL2 - Определяет связь между параметром топологии элемента и переменной
проектирования с использованием уравнения, заданного пользователем.
DVMREL1 - Определяет связь между свойством материала и переменной
проектирования.
DVMREL2 - Определяет связь между свойством материала и переменными
проектирования с использованием уравнения, заданного пользователем.
Слайд 13
Пример №15
Оптимизация с учетом собственных колебаний
Слайд 14
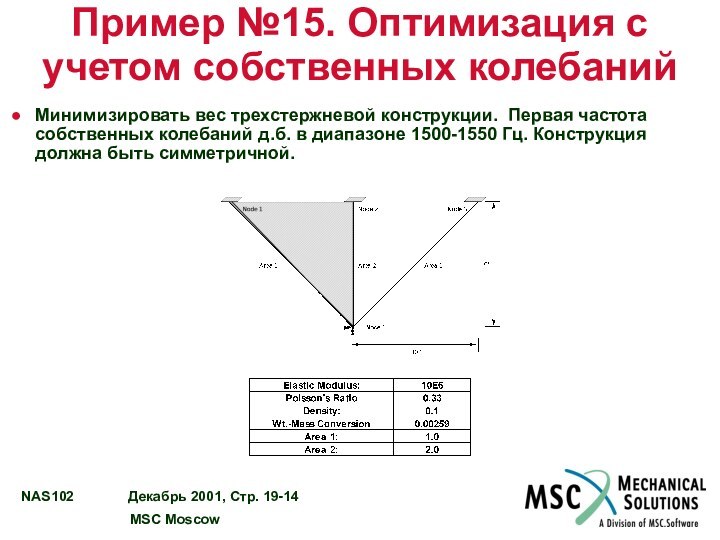
Пример №15. Оптимизация с учетом собственных колебаний
Минимизировать вес
трехстержневой конструкции. Первая частота собственных колебаний д.б. в диапазоне
1500-1550 Гц. Конструкция должна быть симметричной.
Слайд 15
Операторы оптимизации
Переменные проектирования
Площади поперечных сечений элементов ROD (A1,
A2, A3)
Цель
Минимизация веса стержней.
Необходимо выполнение следующих требований:
Первая частота собственных
колебаний д.б. в диапазоне
1500-1550 Гц.
A1 = A3 – условие симметрии конструкции.

для Примера
№15
ID NAS102, WORKSHOP 15
TIME 10
SOL 200 $ OPTIMIZATION
CEND
TITLE= SYMMETRIC THREE BAR TRUSS DESIGN OPTIMIZATION - VARIATION OF D200X1
SUBTITLE= GOAL IS TO MIN WT WHILE KEEPING THE 1ST MODE BETWEEN 1500-1550 HZ
ECHO= SORT
SPC= 100
DISP(PLOT) ALL
DESOBJ(MIN)= 100 $ (DESIGN OBJECTIVE = DRESP ID)
DESSUB= 200 $ DEFINE CONSTRAINT SET FOR BOTH SUBCASES
SUBCASE 1
ANALYSIS= MODES
METHOD= 10
BEGIN BULK
$
$----------------------------------------------------------------------
$ ANALYSIS MODEL
$----------------------------------------------------------------------
$
EIGRL, 10, , , 2
PARAM, POST, -1
$
$ GRID DATA
$ 2 3 4 5 6 7 8 9 10
GRID, 1, , -10.0, 0.0, 0.0
GRID, 2, , 0.0, 0.0, 0.0
GRID, 3, , 10.0, 0.0, 0.0
GRID, 4, , 0.0, -10.0, 0.0
$ SUPPORT DATA
SPC, 100, 1, 123456, , 2, 123456
SPC, 100, 3, 123456, , 4, 3456
$ ELEMENT DATA
CROD, 1, 11, 1, 4
CROD, 2, 12, 2, 4
CROD, 3, 13, 3, 4
$ PROPERTY DATA
PROD, 11, 1, 1.0
PROD, 12, 1, 2.0
PROD, 13, 1, 1.0
MAT1, 1, 1.0E+7, , 0.33, 0.1
$
PARAM, WTMASS, .00259
Слайд 17
Входной файл для Примера №15
$
$----------------------------------------------------------------------
$ DESIGN MODEL
$----------------------------------------------------------------------
$
$...DESIGN VARIABLE
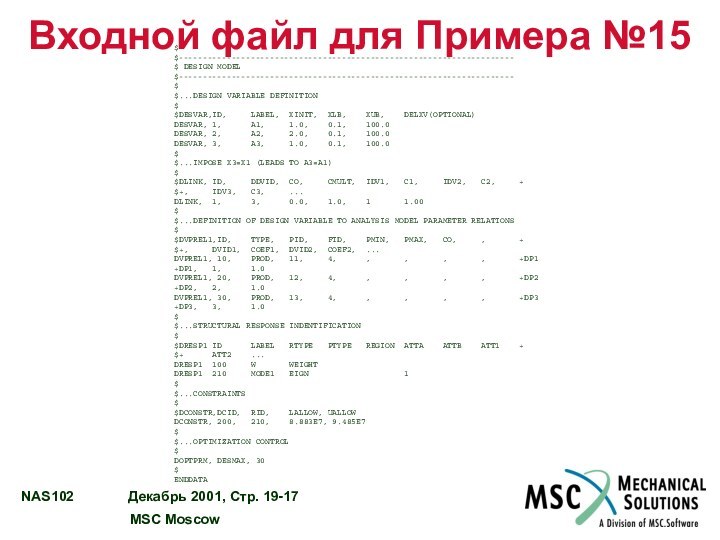
DEFINITION
$
$DESVAR,ID, LABEL, XINIT, XLB, XUB,
DELXV(OPTIONAL)
DESVAR, 1, A1, 1.0, 0.1, 100.0
DESVAR, 2, A2, 2.0, 0.1, 100.0
DESVAR, 3, A3, 1.0, 0.1, 100.0
$
$...IMPOSE X3=X1 (LEADS TO A3=A1)
$
$DLINK, ID, DDVID, CO, CMULT, IDV1, C1, IDV2, C2, +
$+, IDV3, C3, ...
DLINK, 1, 3, 0.0, 1.0, 1 1.00
$
$...DEFINITION OF DESIGN VARIABLE TO ANALYSIS MODEL PARAMETER RELATIONS
$
$DVPREL1,ID, TYPE, PID, FID, PMIN, PMAX, CO, , +
$+, DVID1, COEF1, DVID2, COEF2, ...
DVPREL1, 10, PROD, 11, 4, , , , , +DP1
+DP1, 1, 1.0
DVPREL1, 20, PROD, 12, 4, , , , , +DP2
+DP2, 2, 1.0
DVPREL1, 30, PROD, 13, 4, , , , , +DP3
+DP3, 3, 1.0
$
$...STRUCTURAL RESPONSE INDENTIFICATION
$
$DRESP1 ID LABEL RTYPE PTYPE REGION ATTA ATTB ATT1 +
$+ ATT2 ...
DRESP1 100 W WEIGHT
DRESP1 210 MODE1 EIGN 1
$
$...CONSTRAINTS
$
$DCONSTR,DCID, RID, LALLOW, UALLOW
DCONSTR, 200, 210, 8.883E7, 9.485E7
$
$...OPTIMIZATION CONTROL
$
DOPTPRM, DESMAX, 30
$
ENDDATA
Слайд 18
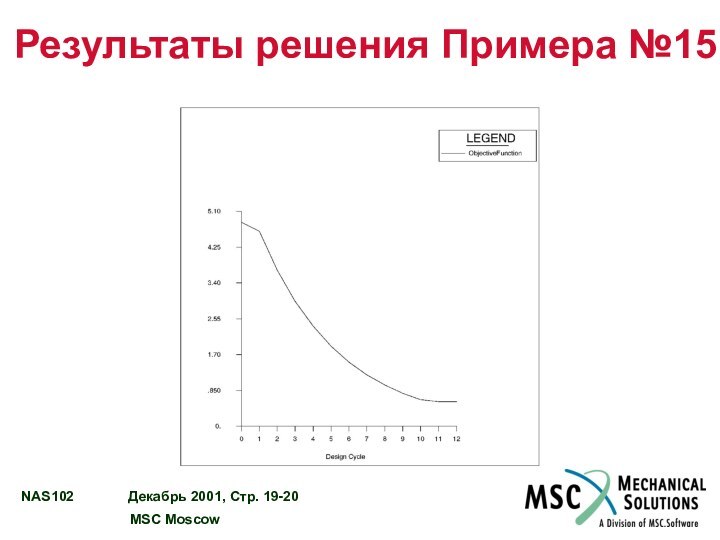
Результаты решения Примера №15
0

SUBCASE 1
***************************************************************
S U M M A R Y O F D E S I G N C Y C L E H I S T O R Y
***************************************************************
(HARD CONVERGENCE ACHIEVED)
(SOFT CONVERGENCE ACHIEVED)
NUMBER OF FINITE ELEMENT ANALYSES COMPLETED 13
NUMBER OF OPTIMIZATIONS W.R.T. APPROXIMATE MODELS 12
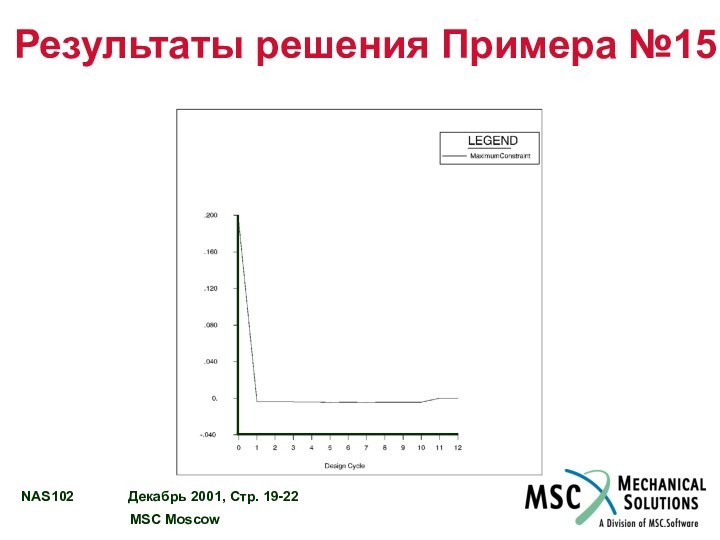
OBJECTIVE AND MAXIMUM CONSTRAINT HISTORY
---------------------------------------------------------------------------------------------------------------
OBJECTIVE FROM OBJECTIVE FROM FRACTIONAL ERROR MAXIMUM VALUE
CYCLE APPROXIMATE EXACT OF OF
NUMBER OPTIMIZATION ANALYSIS APPROXIMATION CONSTRAINT
---------------------------------------------------------------------------------------------------------------
INITIAL 4.828427E+00 1.922634E-01
1 4.624039E+00 4.623868E+00 3.712506E-05 -3.992662E-03
2 3.699272E+00 3.699094E+00 4.795320E-05 -3.992493E-03
3 2.958851E+00 2.959000E+00 -5.019763E-05 -4.089320E-03
4 2.366940E+00 2.367200E+00 -1.099836E-04 -4.089320E-03
5 1.892237E+00 1.892110E+00 6.722458E-05 -4.995593E-03
6 1.514333E+00 1.514324E+00 5.982807E-06 -4.559115E-03
7 1.210749E+00 1.210854E+00 -8.624274E-05 -5.078925E-03
8 9.690658E-01 9.690483E-01 1.808348E-05 -4.686642E-03
9 7.753531E-01 7.752386E-01 1.476971E-04 -4.686642E-03
10 6.202133E-01 6.201910E-01 3.604010E-05 -4.686726E-03
11 5.758922E-01 5.758651E-01 4.699106E-05 -3.288561E-04
12 5.758651E-01 5.758651E-01 0.000000E+00 -3.288561E-04
---------------------------------------------------------------------------------------------------------------
Слайд 19
1 SYMMETRIC THREE BAR TRUSS DESIGN OPTIMIZATION

- VARIATION OF D200 APRIL 22,
1998 MSC.Nastran 4/20/98 PAGE 47
GOAL IS TO MIN WT WHILE KEEPING THE 1ST MODE BETWEEN 1500-1550
0 SUBCASE 1
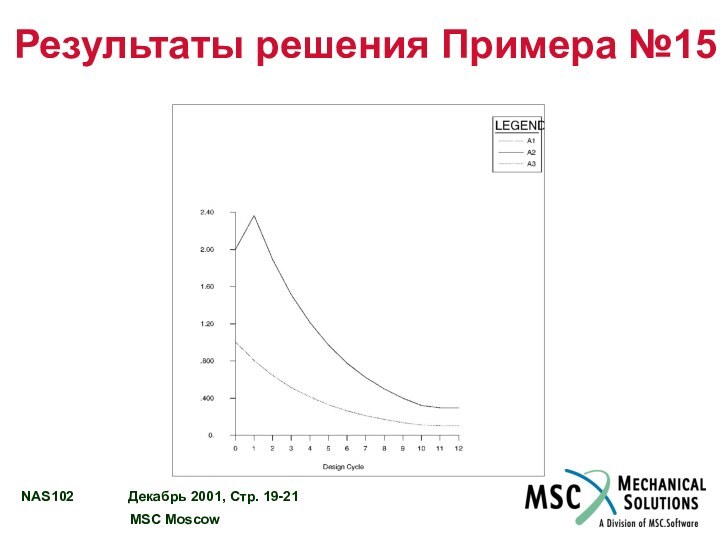
DESIGN VARIABLE HISTORY
----------------------------------------------------------------------------------------------------------------------------------
INTERNAL | EXTERNAL | |
DV. ID. | DV. ID. | LABEL | INITIAL : 1 : 2 : 3 : 4 : 5 :
----------------------------------------------------------------------------------------------------------------------------------
1 | 1 | A1 | 1.0000E+00 : 8.0000E-01 : 6.4000E-01 : 5.1190E-01 : 4.0952E-01 : 3.2703E-01 :
2 | 2 | A2 | 2.0000E+00 : 2.3611E+00 : 1.8889E+00 : 1.5111E+00 : 1.2089E+00 : 9.6712E-01 :
3 | 3 | A3 | 1.0000E+00 : 8.0000E-01 : 6.4000E-01 : 5.1190E-01 : 4.0952E-01 : 3.2703E-01 :
----------------------------------------------------------------------------------------------------------------------------------
INTERNAL | EXTERNAL | |
DV. ID. | DV. ID. | LABEL | 6 : 7 : 8 : 9 : 10 : 11 :
----------------------------------------------------------------------------------------------------------------------------------
1 | 1 | A1 | 2.6185E-01 : 2.0927E-01 : 1.6754E-01 : 1.3403E-01 : 1.0723E-01 : 1.0000E-01 :
2 | 2 | A2 | 7.7369E-01 : 6.1895E-01 : 4.9516E-01 : 3.9613E-01 : 3.1690E-01 : 2.9302E-01 :
3 | 3 | A3 | 2.6185E-01 : 2.0927E-01 : 1.6754E-01 : 1.3403E-01 : 1.0723E-01 : 1.0000E-01 :
----------------------------------------------------------------------------------------------------------------------------------
INTERNAL | EXTERNAL | |
DV. ID. | DV. ID. | LABEL | 12 : 13 : 14 : 15 : 16 : 17 :
----------------------------------------------------------------------------------------------------------------------------------
1 | 1 | A1 | 1.0000E-01 :
2 | 2 | A2 | 2.9302E-01 :
3 | 3 | A3 | 1.0000E-01 :
*** USER INFORMATION MESSAGE 6464 (DOM12E)
RUN TERMINATED DUE TO HARD CONVERGENCE TO AN OPTIMUM AT CYCLE NUMBER = 12.
Результаты решения Примера №15
Слайд 23
Прямое задание широко- используемых функций
Прямое задание широко используемых
функций (например, SUM, RSS, AVG и т.п.) с помощью
оператора DRESP1 для анализа переходного процесса и частотного отклика.
Пример:
DRESP1,100,RSSCAL,FRDISP,,,3,RSS,100
Оператор DRESP1 вычисляет квадратный корень из суммы перемещений узла №100 вдоль оси Z на всех частотах вынуждающей силы.
Слайд 24
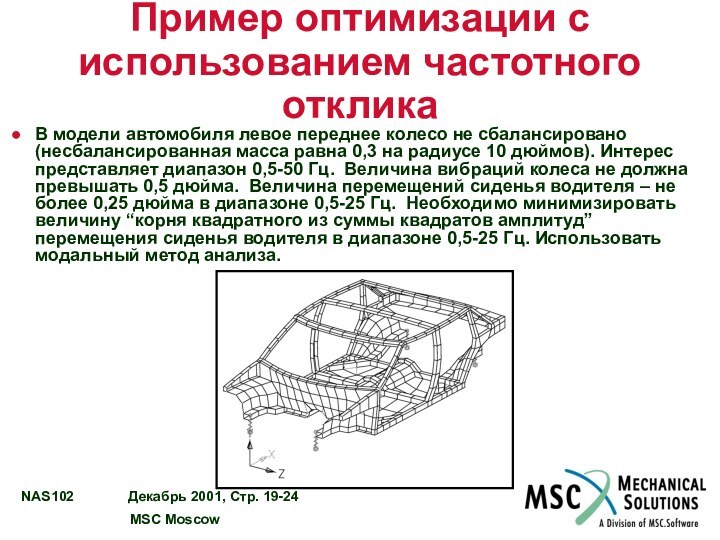
Пример оптимизации с использованием частотного отклика
В модели автомобиля
левое переднее колесо не сбалансировано (несбалансированная масса равна 0,3
на радиусе 10 дюймов). Интерес представляет диапазон 0,5-50 Гц. Величина вибраций колеса не должна превышать 0,5 дюйма. Величина перемещений сиденья водителя – не более 0,25 дюйма в диапазоне 0,5-25 Гц. Необходимо минимизировать величину “корня квадратного из суммы квадратов амплитуд” перемещения сиденья водителя в диапазоне 0,5-25 Гц. Использовать модальный метод анализа.
Слайд 25
Операторы оптимизации
Переменные проектирования:
Параметры жесткости и демпфирования в модели
автомобиля
Цель:
Минимизация величины “корня квадратного из суммы квадратов амплитуд” перемещения
сиденья водителя в диапазоне 0,5-25 Гц
Необходимо выполнение следующих требований:
Максимальные вертикальные перемещения колеса д.б. не более 0,5 дюйма
Максимальные вертикальные перемещения сиденья водителя д.б. не более 0,25 дюйма
Слайд 26
Задание динамических нагрузок
Используем оператор DAREA для задания амплитуд
Fx и Fy (mr)
Используем операторы RLOAD1 для задания каждой
нагрузки
Используем оператор DPHASE для задания фазовых зависимостей
Используем оператор TABLED4 для задания зависимости нагрузки от частоты (w2)
Используем оператор DLOAD для комбинирования нагрузок (RLOAD1’ов)
Направление вращения
F = mr
w
2
q
=
w
t
F
x
= F cos(
w
t)
F
y
= F sin(
w
t)
q
Слайд 27
Оператор TABLED4 для этого примера
Назначим X1 = 0.
X2 = 1. X3 = 0. X4 = 1000.
(более чем достаточно для интересующего диапазона частот)
Поскольку X измеряется в Гц, то для получения его значения в рад/с необходимо учесть множитель 2p
Возбуждающая сила равна mrw2 - введем mr с помощью оператора DAREA, надо, однако, еще w2
Предполагаем получить w2 с помощью оператора TABLED4, что достигается назначением A1=0.0 and A2=(2p)2
Слайд 28
Чувствительность динамического отклика
MSC.Nastran обеспечивает вычисление чувствительности динамического отклика
на изменения переменных проектирования dri/dxj
Знание этих величин позволяет находить
наиболее перспективные направления улучшения конструкции.
Вывод коэффициентов чувствительности инициируется DSAPRT в Case Control Section
Возможные типы анализа:
Анализ частотного отклика прямым методом
Анализ частотного отклика модальным методом
Анализ переходного процесса модальным методом
Слайд 29
Описание “конструкторской” модели
Определение связей свойств расчетной модели с
переменными проектирования (DVPREL1, DVPREL2).
Задание откликов, которые будут использоваться при
оптимизации (DRESP1, DRESP2).
Задание границ изменения откликов и, при необходимости, параметров проверки соблюдения ограничений (DCONSTR, DSCREEN).
Назначение расчетных значений частоты и шага по времени в Case Control Section (OFREQ или OTIME).
Слайд 30
Входной файл для оптимизационной модели
Executive и Case Control
Section
SOL 200
CEND
TITLE = Sample dynamic analysis model
set 999 =
358,471
DISP(phase) = 999
SUBCASE 1
ANALYSIS = MFREQ
DESSUB = 100 $ constraints
DESOBJ(min) = 300 $ design objective - minimize driver’s response
DLOAD = 1
METHOD = 1
FREQ = 1
Bulk Data Section
BEGIN BULK
.
.
include ’car.blk’
include ’springs.blk’
include ’optim1.blk’
.
.
ENDDATA
Слайд 31
Фрагмент файла CAR.BLK
Задание динамического нагружения
EIGRL,1,-1.0,100.
DLOAD,1,1.,1.,11,1.,12
RLOAD1,11,20,,,,111
RLOAD1,12,30,,,40,111
DPHASE 40
358 2 90.
DAREA
20 358 1 3.
DAREA 30 358 2 3.
TABLED4,111,0.,1.,0.,1000.
,0.,0.,39.478,ENDT
$
$ PLUS THE REST OF THE MODEL DESCRIPTION
$
Слайд 32
Фрагмент файла SPRINGS.BLK
Задание упругих элементов (пружин)
CROD 1002
1002 402 1402
CROD
1012 1001 825 1825
CROD 1022 1001 358 1358
CROD 1032 1002 869 1869
$
PROD 1001 1000 1000.
PROD 1002 1000 800.
$ select material so that value of PROD
$ is spring stiffness,
$ therefore, E = l = 10.
MAT1 1000 10.
Задание демпферов (амортизаторов)
$
$ add dampers for shock absorbers
$
$ front
cvisc 2011 2001 825 1825
cvisc 2021 2001 358 1358
$ back
cvisc 2001 2002 402 1402
cvisc 2031 2002 869 1869
$ damper properties
pvisc 2001 10. 0.
pvisc 2002 5. 0.
$
Слайд 33
Фрагмент файла OPTIM.BLK
Задание переменных проектирования
desvar,1,frntdamp,1.,.1,10.
desvar,2,reardamp,1.,.2,20.
desvar,3,frntstif,1.,.4,2.
desvar,4,rearstif,1.,.5,2.5
Задание связей свойств с
переменными проектирования
$
$ relation between properties and variables
$
dvprel1,101,pvisc,2001,3,1.,,,,+dv101
+dv101,1,10.
dvprel1,102,pvisc,2002,3,1.,,,,+dv102
+dv102,2,5.
dvprel1,103,prod,1001,4,4.,,,,+dv103
+dv103,3,10.
dvprel1,104,prod,1002,4,4.,,,,+dv104
+dv104,4,8.
$
Задание ограничений
$ require
that maximum tire displacement be .5 inches
$
dconstr,101,200,-.5,.5
$
$ require that maximum driver displacement be .25 inches
$
dconstr,102,201,-.25,.25
$ combine constraints into set 100
$
dconadd,100,101,102
Слайд 34
Фрагмент файла OPTIM.BLK
Задание откликов, используемых при оптимизации
$ select
displacement Y at driver seat and mount point as
$
response quantities
$
$ mount point
$
dresp1,200,disp,frdisp,,,2,,358
$
$ define driver’s seat disp as a response
$
dresp1,201,driver,frdisp,,,2,,471
Задание целевой функции - величины “корня квадратного из суммы квадратов амплитуд” перемещения сиденья водителя в диапазоне 0,5-25 Гц
dresp1,300,srss,frdisp,,,2,RSS,471
Слайд 35
Пример №16
Оптимизация с использованием частотного отклика
Слайд 36
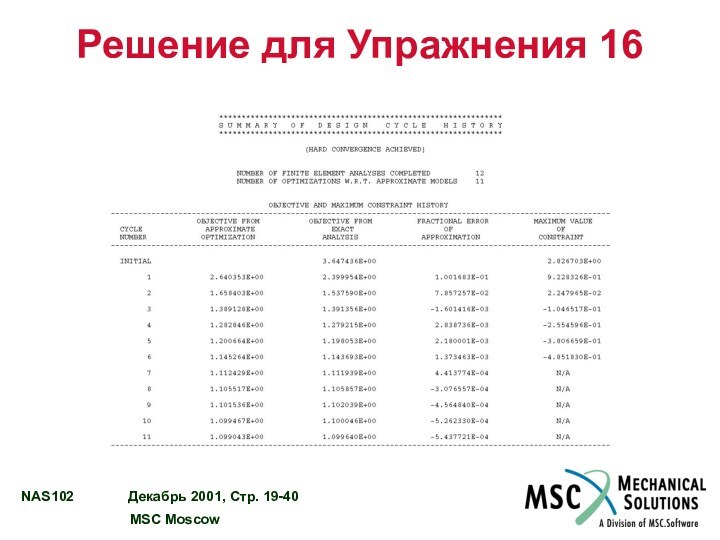
Решение для Упражнения 16
$
$ input file to
optimize (minimize) the response of a car to a
$ rotating imbalance - V68 - June, 1994
$ use modal approach - up to 100 hz
$
SOL 200
diag 8
CEND
TITLE = Sample dynamic analysis model
SUBTITLE = Rotating force due to tire out of balance
LABEL = perform optimization to minimize driver response
set 999 = 358,471
DISP(phase) = 999
SUBCASE 1
ANALYSIS = MFREQ
DESSUB = 100 $ constraints
DESOBJ(min) = 300 $ design objective - minimize driver response
DLOAD = 1
METHOD = 1
FREQ = 1
BEGIN BULK
eigrl,1,0.,100.
doptprm,desmax,25
include ’car.blk’
include ’springs.blk’
include ’optim1.blk’
param,post,0
$
$
$ DATA RELATED TO FREQUENCY RESPONSE
$
DLOAD 1 1. 1. 11 1. 12
RLOAD1 11 20 111
RLOAD1 12 30 40 111
DPHASE 40 358 2 90.
DAREA 20 358 1 3.
DAREA 30 358 2 3.
TABLED4 111 0. 1. 0. 100.
0. 39.478 ENDT
FREQ1 1 .5 .5 100
$
ENDDATA
Слайд 37
Решение для Упражнения 16
$
$ springs.blk
$
CONM2

3001 1402 1.E8
CONM2
3002 1825 1.E8
CONM2 3003 1358 1.E8
CONM2 3004 1869 1.E8
$
GRID 1402 159.870 11.0000 -14.3750 13456
GRID 1358 20.6116 11.0000 -15.1000 13456
GRID 1825 20.6116 11.0000 -54.9000 13456
GRID 1869 159.870 11.0000 -55.6250 13456
$
CELAS2 1001 10000. 402 1 1402 1
CROD 1002 1002 402 1402
CELAS2 1003 10000. 402 3 1402 3
CELAS2 1011 10000. 825 1 1825 1
CROD 1012 1001 825 1825
CELAS2 1013 10000. 825 3 1825 3
CELAS2 1021 10000. 358 1 1358 1
CROD 1022 1001 358 1358
CELAS2 1023 10000. 358 3 1358 3
CELAS2 1031 10000. 869 1 1869 1
CROD 1032 1002 869 1869
CELAS2 1033 10000. 869 3 1869 3
$
$ properties for springs
$
PROD 1001 1000 1000.
PROD 1002 1000 800.
$ select material so that value of PROD is spring stiffness,
$ therefore, E = l = 10.
MAT1 1000 10.
$
$ add dampers for shock absorbers
$ front
cvisc 2011 2001 825 1825
cvisc 2021 2001 358 1358
$ back
cvisc 2001 2002 402 1402
cvisc 2031 2002 869 1869
$ damper properties
pvisc 2001 10. 0.
pvisc 2002 5. 0.
$
$ end of springs.blk
$
Слайд 38
Решение для Упражнения 16
$
$ file -
car.blk
$
$ MODEL COURTESY LAPCAD ENGINEERING
$
CHULA VISTA, CALIFORNIA
$
GRID 1 79.0000 56.0000-2.00000
GRID 2 157.000 40.1000-1.30000
.
.
CQUAD4 29 2 22 19 12 21 0.00E+0 0.00E+0
CQUAD4 30 2 21 20 11 22 0.00E+0 0.00E+0
.
.
PSHELL 1 1 0.025 1
PSHELL 2 1 0.200 1
.
.
MAT1 11.000E+73.759E+63.300E-12.600E-41.370E-57.000E+1.3
$
$ end of car.blk
$
Слайд 39
Решение для Упражнения 16
$
$ beginning of optim1.blk
$
$

data for design sensitivity
$
$ define design variables
$
desvar,1,frntdamp,1.,.1,10.
desvar,2,reardamp,1.,.2,20.
desvar,3,frntstif,1.,.4,2.
desvar,4,rearstif,1.,.5,2.5
$
$ relation
between properties and variables
$
dvprel1,101,pvisc,2001,3,1.,,,,+dv101
+dv101,1,10.
dvprel1,102,pvisc,2002,3,1.,,,,+dv102
+dv102,2,5.
dvprel1,103,prod,1001,4,4.,,,,+dv103
+dv103,3,10.
dvprel1,104,prod,1002,4,4.,,,,+dv104
+dv104,4,8.
$
$
$ select displacement Y at tire and driver seat as
$ response quantities
$
$ maximum tire displacement be < +/-0.5 inches
$
dconstr,101,200,-.5,.5
dresp1,200,disp,frdisp,,,2,,358
$
$ define driver's seat disp as a response
$
$
$ require that maximum driver displacement be < +/- 0.25 inches
$ between .5 and 25 hz
$
dconstr,102,201,-.25,.25,0.5,25.0
dresp1,201,driver,frdisp,,,2,,471
$
$ combine constraints into set 100
$
dconadd,100,101,102
$
$ define objective = minimize srss of response
$
dresp1,300,rss,frdisp,,,2,rss,471
$
$ end of optimization input
$
$ end of optim1.blk
$
Слайд 42
Результаты решения задачи оптимизации
Решение получено за 11 шагов.
Результаты
решения:
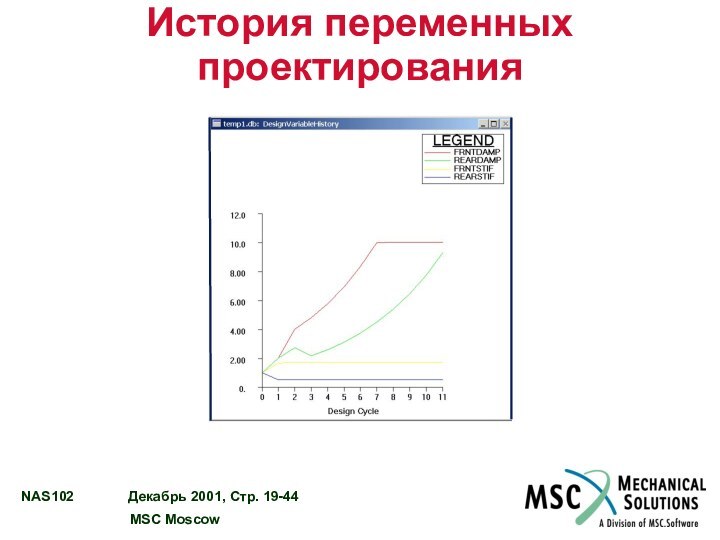
Слайд 44
История переменных проектирования
Слайд 45
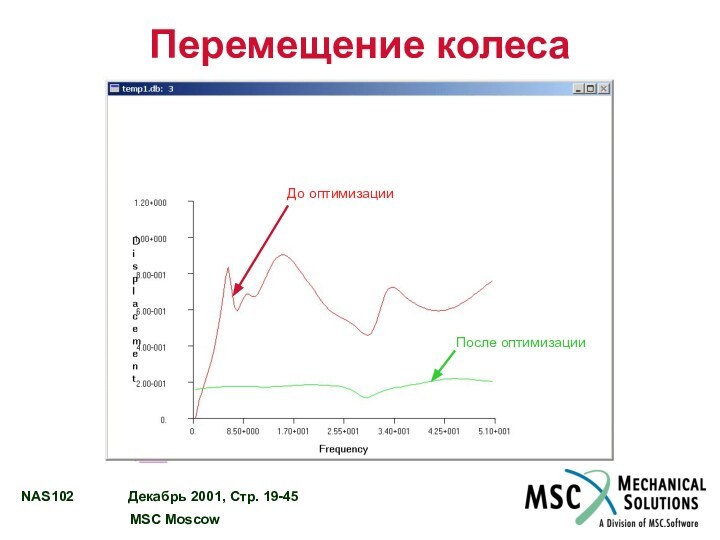
Перемещение колеса
До оптимизации
После оптимизации
Слайд 46
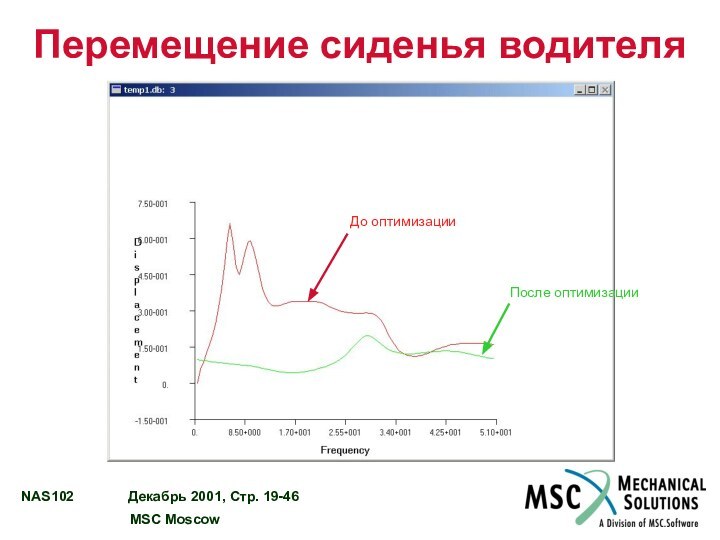
Перемещение сиденья водителя
До оптимизации
После оптимизации
Слайд 47
Заключение
С минимальными усилиями конструкция модифицируется с целью удовлетворения
заданным требованиям и минимизации указанного динамического параметра.
SOL 200 –
ценный инструмент динамического анализа.