Слайд 2
Этапы развития логики
I этап - формальная логика.
Основатель
- Аристотель
(384-322 гг. до н.э.),
ввел основные формы
абстрактного мышления.
II этап – математическая логика.
Основатель – немецкий ученый
и философ Лейбниц
(1642-1716), предпринял попытку
логических вычислений.
III этап – математическая логика
(булева алгебра).
Основатель – английский
математик Джордж Буль
(1815-1864),
ввел алфавит,
орфографию и грамматику
для математической логики.
Историческая справка
Слайд 3
Законы логики
отражают в сознании
человека свойства,
связи
и отношения
объектов окружающего
мира.
Логика изучает
внутреннюю структуру
процесса
мышления,
который реализуется
в следующих формах:
понятие
высказывание (суждение)
умозаключение
доказательство
Логика-наука, изучающая законы и формы мышления
Слайд 4
Формы мышления
Умозаключение –
из одного или нескольких
суждений
(посылок)
по определенным правилам
логического вывода
получается новое
суждение (заключение)
Высказывание (суждение)
выражается
повествовательным
предложением на основе
понятий, в котором что-либо
утверждается или отрицается
о свойствах реальных
предметах и отношениях
между ними
Понятие выделяет
существенные признаки
объекта, отличающие
его от других объектов
Содержание –
совокупность
существенных
признаков объекта
Объем понятия
(множество объектов) –
совокупность
предметов, на которую
распространяется
понятие
равнозначность
пересечение
подчинение
Дедуктивные -
от общего к частному
Доказательство –
подтверждение
или опровержение
какого – либо положения
посредством
других, ранее
обоснованных доводов
Индуктивные -
от частного к общему
По аналогии -
от общности одних
свойств и отношений
у сравниваемых предметов
или процессов к общности других
Слайд 5
Какие из предложений являются высказываниями:
Число 6 – четное.
Посмотрите
на доску.
Все роботы являются машинами.
У каждой лошади есть хвост.
Внимание!
Кто
отсутствует?
Есть кошки, которые дружат с собаками.
Не все то золото, что блестит.
Х2>=0
Некоторые люди являются художниками.
Выразите 1 час 50 минут в минутах.
Всякий моряк умеет плавать.
Электрон – элементарная частица.
Слайд 6
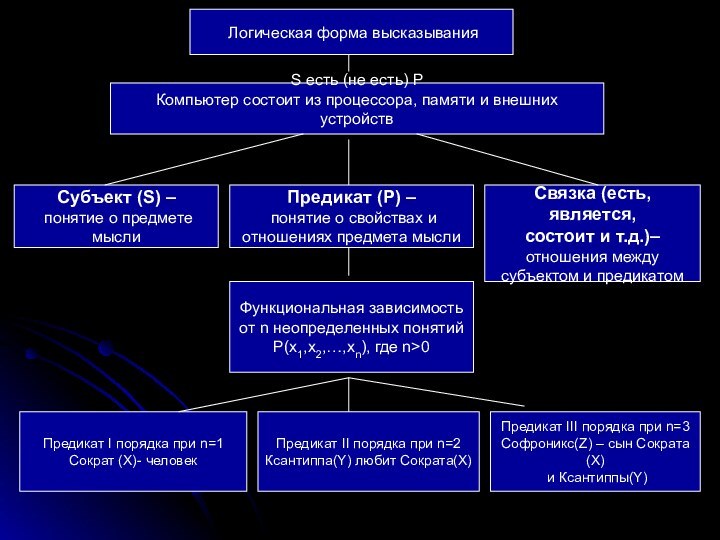
Логическая форма высказывания
Связка (есть, является,
состоит и
т.д.)–
отношения между
субъектом и предикатом
Субъект (S) –
понятие
о предмете мысли
Предикат (P) –
понятие о свойствах и
отношениях предмета мысли
Функциональная зависимость
от n неопределенных понятий
P(x1,x2,…,xn), где n>0
Предикат II порядка при n=2
Ксантиппа(Y) любит Сократа(X)
Предикат III порядка при n=3
Софроникс(Z) – сын Сократа(X)
и Ксантиппы(Y)
Предикат I порядка при n=1
Сократ (X)- человек
S есть (не есть) P
Компьютер состоит из процессора, памяти и внешних устройств
Слайд 7
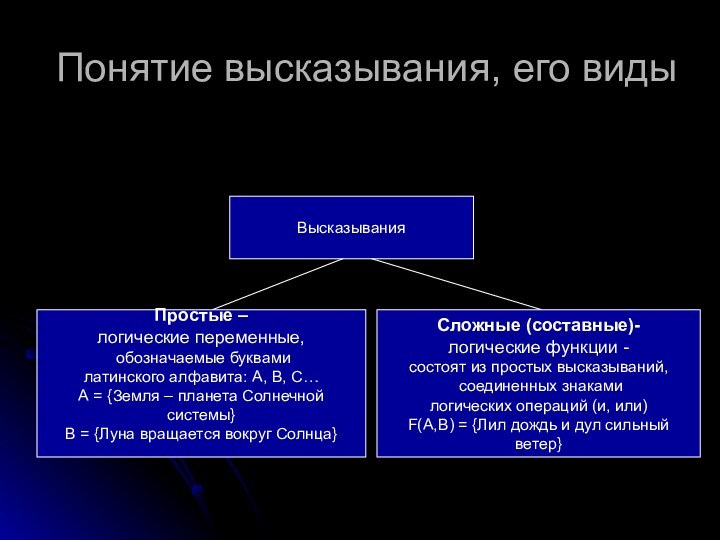
Понятие высказывания, его виды
Слайд 8
Из двух простых высказываний постройте сложное высказывание, используя
логические связки «И», «ИЛИ»
Все ученики изучают математику. Все ученики изучают литературу.
Одна половина класса изучает английский язык. Одна половина класса изучает немецкий язык.
Марина старше Светы. Оля старше Светы.
В кабинете есть учебники. В кабинете есть справочники.
Часть туристов любит чай. Остальные туристы любят молоко.
Х=3, Х>2
Синий кубик меньше красного. Синий кубик меньше зеленого.
Слова в этом предложении начинаются на букву Ч. Слова в этом предложении начинаются на букву А.
Слайд 9
Высказывания
Частные можно начать со слов:
некоторые
большинство
Некоторые медведи
– бурые.
Общие с можно начать со слов:
все
всякий
каждый
ни один
Все рыбы умеют плавать.
Единичные используются
в единственном числе.
Буква А – гласная.
Слайд 10
Определите общие, частные и единичные высказывания:
Не все книги
содержат полезную информацию.
Кошка является домашним животным.
Все солдаты храбрые.
Ни один
внимательный человек не совершит оплошность.
Некоторые ученики – двоечники.
Все ананасы приятны на вкус.
Мой кот страшный забияка.
Любой неразумный человек ходит на руках.
Некоторые мои друзья собирают марки.
Все лекарства неприятны на вкус.
У некоторых змей нет ядовитых зубов.
Многие растения обладают целебными свойствами.
Все металлы проводят тепло.
Слайд 11
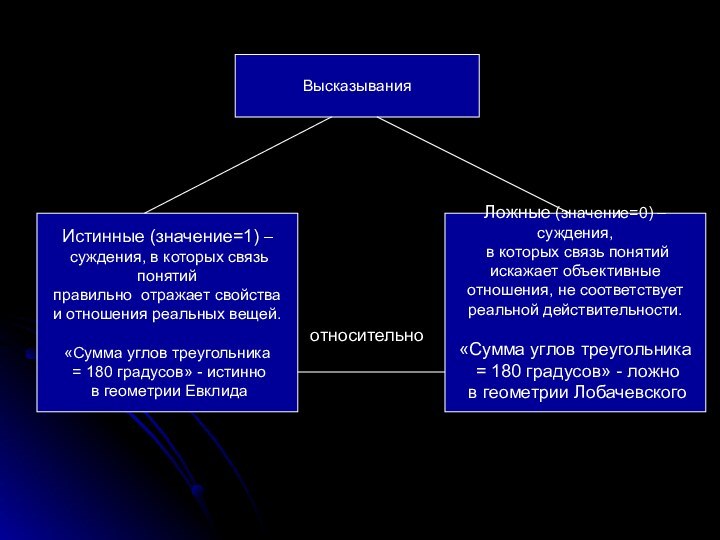
Ложные (значение=0) – суждения,
в которых связь понятий
искажает объективные
отношения, не соответствует
реальной действительности.
«Сумма углов треугольника
= 180 градусов» - ложно
в геометрии Лобачевского
Истинные (значение=1) –
суждения, в которых связь понятий
правильно отражает свойства
и отношения реальных вещей.
«Сумма углов треугольника
= 180 градусов» - истинно
в геометрии Евклида
Высказывания
относительно
Слайд 12
Определите истинность высказываний:
Лед – твердое состояние воды.
Париж –
столица Китая.
Наполеон был французским королем.
Не нарушайте правил дорожного движения!
Каждый
человек – художник.
Прямоугольник – это параллелограмм, у которого все углы прямые.
Человек все может.
Тигр – хищное животное.
Некоторые лекарства приятны на вкус.
Невозможно создать вечный двигатель
Слайд 13
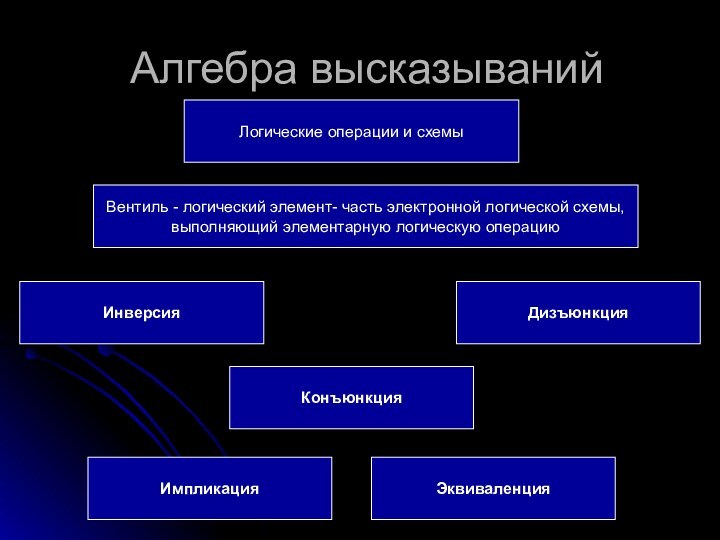
Алгебра высказываний
Логические операции и схемы
Конъюнкция
Импликация
Эквиваленция
Инверсия
Дизъюнкция
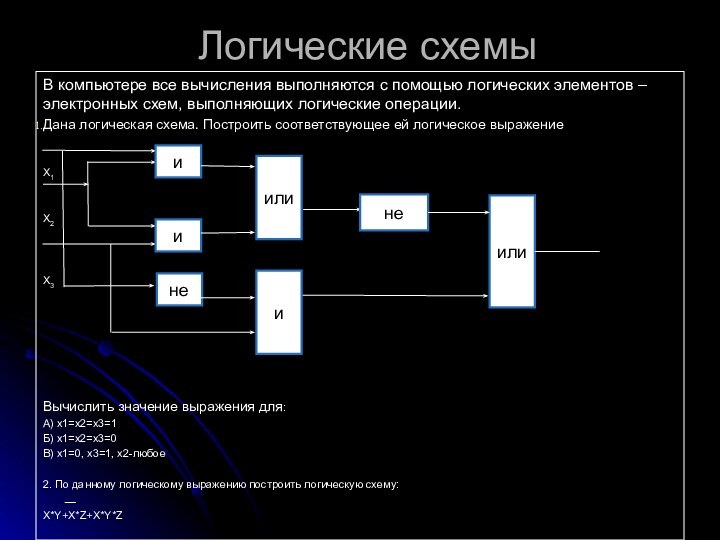
Вентиль - логический элемент-
часть электронной логической схемы,
выполняющий элементарную логическую операцию
Слайд 14
Инверсия (от лат. Inversio – переворачиваю) отрицание
Соответствует
частице НЕ, словосочетанию НЕВЕРНО, ЧТО
Обозначение: не А, А,
А
Таблица истинности:
Логическая схема (инвертор):
Диаграмма Эйлера - Венна
Пример: А = {На улице идет снег}
А = {Неверно, что на улице идет снег}
А = {На улице не идет снег}
А
А
А
А
Слайд 15
Дизъюнкция (от лат. disjunctio -разделение) логическое сложение
Соответствует союзу ИЛИ
Обозначение: +, V, or
Таблица
истинности:
Логическая схема (дизъюнктор):
Диаграмма Эйлера – Венна:
Пример: А = {Ученик вчера в 6 часов вечера читал книгу}
В = {Ученик вчера ехал в автобусе на стадион}
F =АvB = {Ученик вчера в 6 часов вечера читал книгу или ехал в автобусе на стадион}
А
В
F=А+В
Дизъюнкция – это логическая операция,
ставящая в соответствие каждым
двум простым высказываниям
составное высказывание, являющееся
ложным тогда и только тогда,
когда оба исходных высказывания
ложны и истинным, когда хотя бы
одно из двух образующих
его высказываний истинно.
1
Слайд 16
Конъюнкция (от лат. сonjunctio -соединение) логическое умножение
Соответствует
союзу И
Обозначение: *, &, and, ^
Таблица
истинности:
Логическая схема (конъюнктор):
Диаграмма Эйлера – Венна:
Пример: А = {Ученик вчера в 6 часов вечера читал книгу}
В = {Ученик вчера ехал в автобусе на стадион}
F =А&B = {Ученик вчера в 6 часов вечера читал книгу и ехал в автобусе на стадион}
А
В
F=А*В
А
В
Конъюнкция – это логическая операция,
ставящая в соответствие каждым
двум простым высказываниям
составное высказывание, являющееся
истинным тогда и только тогда,
когда оба исходных
высказывания истинны.
&
Слайд 17
Импликация (от лат. implicatio – тесно связаны) логическое
следование
Соответствует обороту: если…, то; из… следует; … влечет
…
Обозначение: , ⇒
Таблица истинности:
Пример: А = {Данный четырехугольник - квадрат}
В = {Около квадрата можно описать окружность }
F =А ⇒ B = {Если данный четырехугольник – квадрат, то около него можно описать окружность }
Импликация – это логическая операция,
ставящая в соответствие каждым
двум простым высказываниям
составное высказывание, являющееся
ложным тогда и только тогда,
когда из истинного условия
следует ложное заключение.
Слайд 18
Эквиваленция (от лат. aeguivalens – равноценные) логическая равнозначность
Соответствует обороту: тогда и только тогда, необходимо и достаточно,
… равносильно…
Обозначение: , ⇔, ~
Таблица истинности:
Пример: А = {Я пойду гулять}
В = {Выучу все уроки}
F =А ⇔ B = {Я пойду гулять тогда и только тогда, когда выучу все уроки}
Эквиваленция – это логическая операция,
ставящая в соответствие каждым
двум простым высказываниям
составное высказывание, являющееся
истинным тогда и только тогда,
когда оба исходных высказывания
одновременно истинны или
одновременно ложны.
Слайд 19
Запишите с помощью логических операций каждое высказывание:

а) Число 376 четное и трехзначное.
б) Неверно, что Солнце движется вокруг Земли.
в) Рыбу ловят сачком, или ловят крючком, или мухой приманивают, иль червячком.
г) Если сумма цифр делится на 3, то число делится на 3.
д) Компьютер может производить вычисления тогда и только тогда, когда он включен.
Найдите значения логических выражений:
а) (1v1)v(1v0) б) ((1v0)v1)v1 в)(0v1)v(1v0) г) (0&1)&1 д) 1&(1&1)&0 е) ((1v0)&(1&1))&(0v1)
3. Даны простые высказывания:
А = {Принтер – устройство ввода информации} В = {Процессор – устройство обработки информации
С = (Монитор – устройство хранения информации) D = {Клавиатура – устройство ввода информации)
Определите истинность высказываний: а) А б) В в) А & В г ) C v D д) A⇒B е ) C⇔D
ж) (A&B)&(C v D)
4. Используя логические операции, запишите высказывания, которые являются истинными при выполнении следующих условий:
а) Х, Y,Z равны между собой;
б) хотя бы одно из чисел Х, Y,Z положительно;
в) только одно из чисел Х, Y,Z больше 10;
г) каждое из чисел равно 0.
5. Запишите на языке алгебры логики следующие высказывания:
а) Я поеду в Киев и если встречу там друзей, то мы интересно проведем время.
б) Если я поеду в Киев и встречу там друзей, то мы интересно проведем время.
в) Неверно, что если погода пасмурная, то идет дождь тогда и только тогда, когда нет ветра.
6. Определите значения логических переменных a, b, c, d, если:
а) а * (Марс - планета) = 1 б) b * (Марс - планета) = 0 в) с + (Солнце – спутник Земли) = 1
г) d + (Солнце – спутник Земли) = 0
7. Определите значения логического выражения не (Х >Z ) и не (X=Y), если:
а) Х=3, Y=5, Z=2 б) Х=0, Y=1, Z=19 в) Х=9, Y=-9, Z=9
Слайд 20
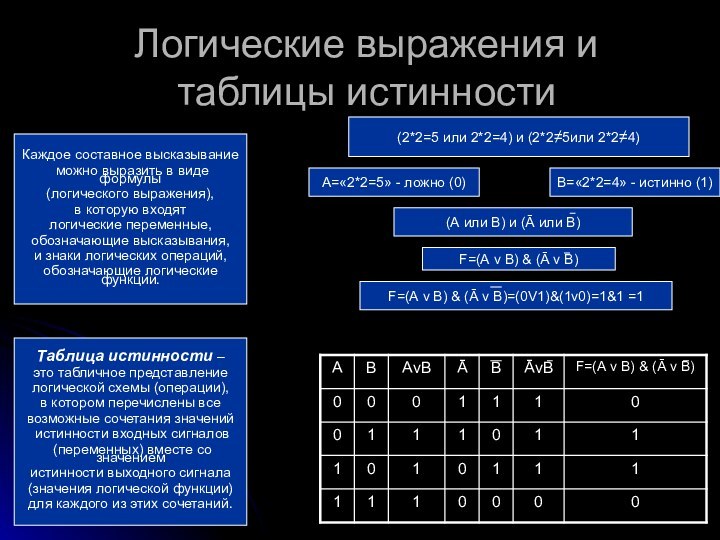
Логические выражения и таблицы истинности
Каждое составное высказывание
можно
выразить в виде формулы
(логического выражения),
в которую входят
логические
переменные,
обозначающие высказывания,
и знаки логических операций,
обозначающие логические функции.
(2*2=5 или 2*2=4) и (2*2≠5или 2*2≠4)
В=«2*2=4» - истинно (1)
А=«2*2=5» - ложно (0)
(А или В) и (Ā или В)
F=(А v В) & (Ā v В)
F=(А v В) & (Ā v В)=(0V1)&(1v0)=1&1 =1
Таблица истинности –
это табличное представление
логической схемы (операции),
в котором перечислены все
возможные сочетания значений
истинности входных сигналов
(переменных) вместе со значением
истинности выходного сигнала
(значения логической функции)
для каждого из этих сочетаний.
Слайд 21
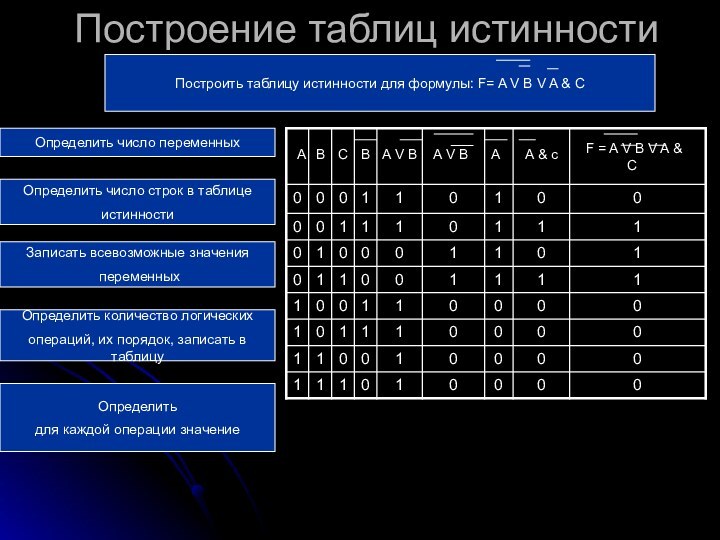
Построение таблиц истинности
Определить число переменных
Записать всевозможные значения
переменных
Определить
число строк в таблице
истинности
Определить количество логических
операций, их
порядок, записать в таблицу
Определить
для каждой операции значение
А
B
С
Слайд 22
Постройте таблицы истинности для следующих функций:
F = (A v B)&(A&B)
F=A ~ B v A ⇒ B
F = A v B&C F = C&D ⇒B
2. Докажите , используя таблицы истинности, что логические выражения равносильны:
а) А v B и A&B, б) А→В и А v B, в) А ~ В и (А & B) v (A & B)
Для формулы A & (B v B & C) постройте таблицу истинности с использованием электронных таблиц.
Дан фрагмент таблицы истинности выражения F. Какие из этих выражений могут соответствовать F
а) X + Y + Z
б) X & Y & Z
в) X + Y + Z
г) X + Y & Z
Слайд 24
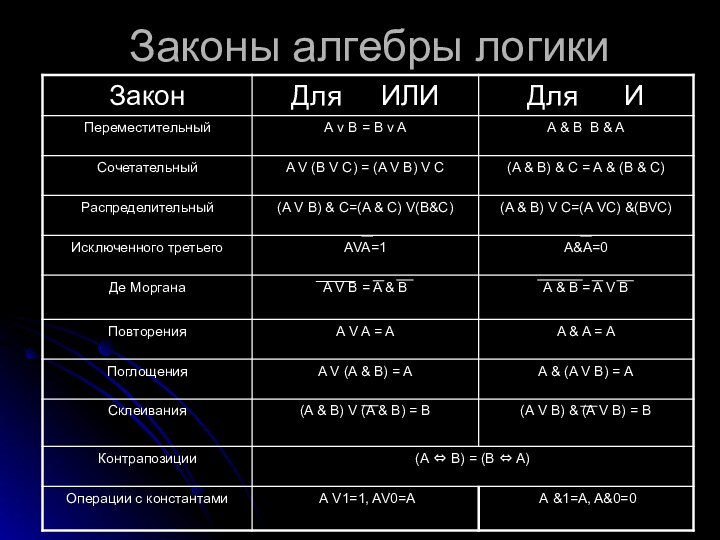
Упрощение логических выражений
Закон де Моргана
Распределительный для сложения
Исключение третьего
1.
Упростите логические выражения:
(А V Ā) & В
b) A & (A V B) & (B V B)
2. Докажите, что выражение тождественно – ложно, тождественно-истинно:
а) В & C V ( A & C →B)
б) А & (A ⇔C) →(A V B)
Исключения констант
Слайд 25
Решение логических задач
1. Решение логических задач средствами алгебры

логики:
Изучить условие задачи
Выделить простые логические высказывания и ввести обозначения
Записать
условие задачи на языке алгебры логики
Составить конечную формулу, объединив логическим умножением формулы каждого утверждения , приравнять произведение единице
Упростить формулу, проанализировать полученный результат или составить таблицу истинности, найти по таблице значения переменных, для которых F=1, проанализировать полученный результат .
2. Решение логических задач табличным способом:
При использовании этого способа условия, которые содержит задача, и результаты рассуждений фиксируются с помощью специально составленных таблиц.
3. Решение логических задач с помощью рассуждений
Этим способом обычно решают несложные логические задачи.
Решите задачи:
1. Три дочери писательницы Жаклин Деманж – Дениз, Амели и Лилиан тоже очень талантливы. Они приобрели известность в разных видах искусств – оперном пении, балете и игре на виолончели. Все они живут в разных городах, поэтому Жаклин часто звонит им в Париж, Рим и Чикаго. Известно что:
Дениз живёт не в Париже, а Лилиан – не в Риме
Парижанка не играет на виолончели
Та, кто живёт в Риме, оперная певица
Лилиан равнодушна к балету
Где живёт Амели и какова её профессия?
2. Трое друзей, болельщиков автогонок "Формула-1", спорили о результатах предстоящего этапа гонок.
— Вот увидишь, Шумахер не придет первым, — сказал Джон. Первым будет Хилл.
— Да нет же, победителем будет, как всегда, Шумахер, — воскликнул Ник. — А об Алези и говорить нечего, ему не быть первым.
Питер, к которому обратился Ник, возмутился:
— Хиллу не видать первого места, а вот Алези пилотирует самую мощную машину.
По завершении этапа гонок оказалось, что каждое из двух предположений двоих друзей подтвердилось, а оба предположения третьего из друзей оказались неверны. Кто выиграл этап гонки?
3. Вадим, Сергей и Михаил изучают различные иностранные языки: китайский, японский и арабский. На вопрос, какой язык изучает каждый из них, один ответил: "Вадим изучает китайский, Сергей не изучает китайский, а Михаил не изучает арабский". Впоследствии выяснилось, что в этом ответе только одно утверждение верно, а два других ложны. Какой язык изучает каждый из молодых людей?