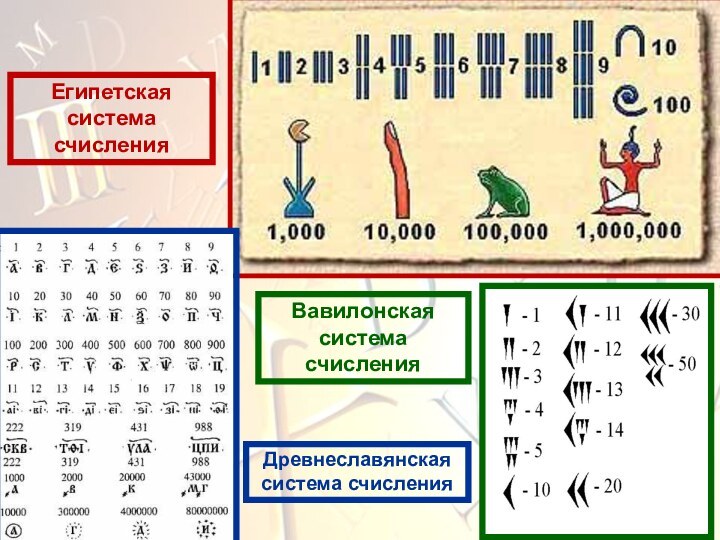
страны, а потом в Западную Европу. Простые и удобные
правила сложения и вычитания очень больших чисел, записанной в этой системе, сделали ее особенно популярной.
Эти правила вывел азиатский математик аль-Хорезми. А поскольку его труд был написан на арабском языке, то и Индийская нумерация в Европе закрепилась неправильным названием "арабское".
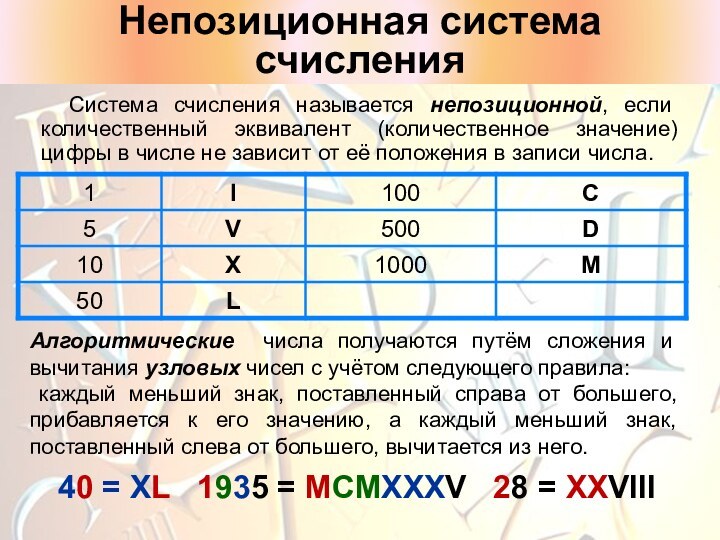
Цифры 1,2,3,4,5,6,7,8,9,0 сложились в Индии. Древнейшая запись обнаружена в Индии и датируется 595г.
Древнее изображение десятичных цифр не
случайно: каждая цифра обозначает число по
количеству углов в ней. Например, 0 – углов нет,
2 – два угла и т.д. Написание десятичных цифр претерпело существенные изменения.
Форма, которой мы пользуемся,
установилась в XVI веке.

























![Представление числовой информации с помощью систем счисления Список источников содержания и иллюстрацийhttp://school-collection.edu.ru/catalog/res/402b749c-240b-4e16-9e4d-bea3fc4fa8fa/?from=a30a9550-6a62-11da-8cd6-0800200c9a66&interface=catalog&class=51&subject=19&rub_guid[]=a30a9550-6a62-11da-8cd6-0800200c9a66 – История развития систем счисленияhttp://school-collection.edu.ru/catalog/res/a96df437-5ae3-4cab-8c5f-8d4cd78c5775/?from=a30a9550-6a62-11da-8cd6-0800200c9a66&interface=catalog&class=51&subject=19&rub_guid[]=a30a9550-6a62-11da-8cd6-0800200c9a66 - Развернутая форма записи числаhttp://go.mail.ru/http://go.mail.ru/ https://ru.wikipedia.orghttp://inf1.info/scalenotation](/img/tmb/12/1100748/86d78ca297f8ac12571726f86bed7f97-720x.jpg)





























