Презентация на тему Рекурсивное программирование

Он ее любил. …
посмотреть… встаньте между двумя зеркалами и смотрите…(не детали гардероба, нет. Отражение себя, там …)
нарисовать… нарисуйте себя, где на полотне вы рисуете себя, где на полотне…

Ее можно:

Это примеры «бесконечной» рекурсии…

factorial(n: integer): longint;
Begin
If n = 1

then factorial:=1
else factorial:= n * factorial (n – 1);
End;

При использовании рекурсии необходимо обеспечить выход из подпрограммы в нужный момент, т.к. алгоритм должен быть конечным (одно из свойств).

программы.
Например, α:= factorial(5)
Function factorial
Begin
factorial:= 5

* factorial(4);
End;

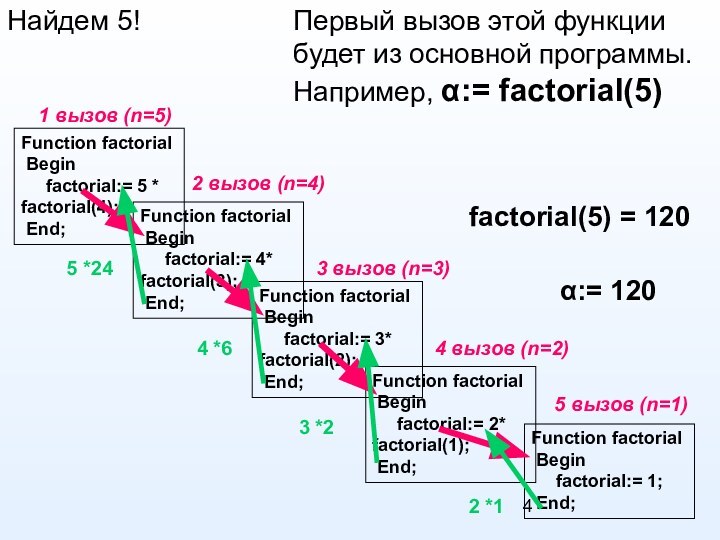
Function factorial
Begin
factorial:= 4* factorial(3);
End;

Function factorial
Begin
factorial:= 2* factorial(1);
End;

Function factorial
Begin
factorial:= 3* factorial(2);
End;

Function factorial
Begin
factorial:= 1;
End;

3 вызов (n=3)

2 вызов (n=4)

4 вызов (n=2)

5 вызов (n=1)

1 вызов (n=5)

2 *1

5 *24

4 *6

3 *2

factorial(5) = 120

α:= 120

чисел:
Sn = Sn-1 + n;

S1 = 1.

2. Составить рекурсивную программу ввода с клавиатуры последовательность чисел (окончание ввода - 0) и вывода ее на экран в обратном порядке.

в двоичную.
3910 = 1001112
Procedure Rec(n: integer);
begin

If n > 1 then Rec(n Div 2);
Write(n Mod 2);
End;

Write(n Mod 2);
End;
1 вызов (n = 39)
Procedure Rec
begin

Rec(n Div 2);
Write(n Mod 2);
End;

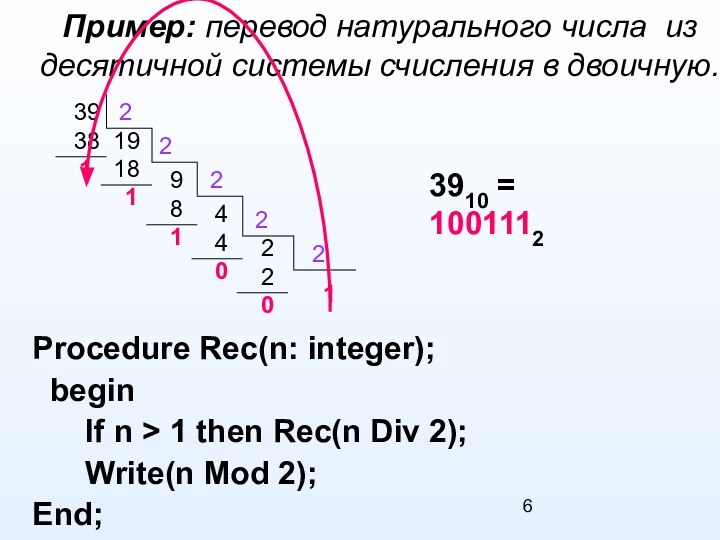
Procedure Rec
begin
Rec(n Div 2);
Write(n Mod 2);
End;

Procedure Rec
begin
Rec(n Div 2);
Write(n Mod 2);
End;

Procedure Rec
begin
Rec(n Div 2);
Write(n Mod 2);
End;

Procedure Rec
begin
Write(n Mod 2);
End;

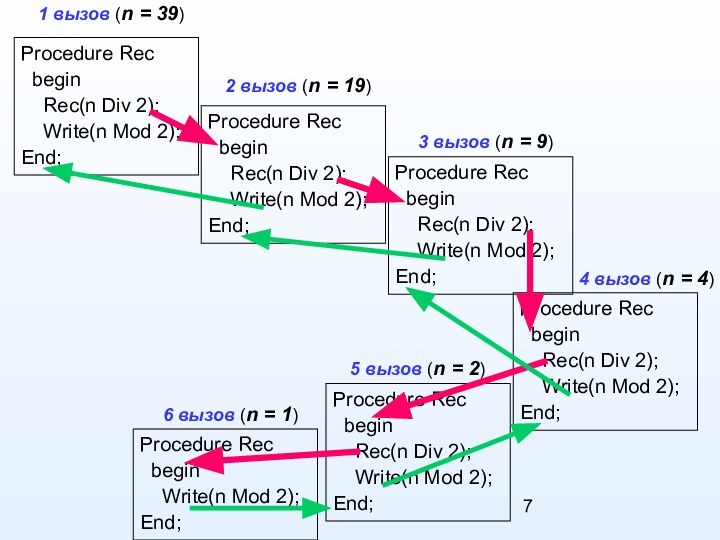
2 вызов (n = 19)

3 вызов (n = 9)

4 вызов (n = 4)

6 вызов (n = 1)

5 вызов (n = 2)

N - ю, при условии, что 2 ≤

N ≥ 16 и его значение вводится с клавиатуры.
Каким будет условие завершения входа в рекурсию?

Каждое число равно сумме двух предыдущих чисел при условии,

что первые два равны 1 (1, 1, 2, 3, 5, 8, 13, 21, …).
Рекурсивная постановка данной задачи:

if (nf=1) or (nf=2) then fib:=1
else

fib:=fib(nf-1)+fib(nf-2);
end;
begin
readln(n);
for i:=1 to n do
writeln(fib(i));
end.

Данная программа раскрывает недостатки рекурсии:
с увеличением n глубина рекурсии многократно (во сколько?) увеличивается и выполняемая программа потребует много памяти, что может привести к переполнению стека.
Если при решении есть выбор между итерацией и рекурсией, то предпочтительным выбором является итерация.

пока не будет удовлетворяться некоторое условие.
Большинство алгоритмов можно

реализовать двумя способами:

function fibon(nf:integer):longint;
begin
f1:=1; f2:=1;
for i:=3 to n do
begin f:=f1+f2;
f1:=f2; f2:=f;
end;
fibon:=f;
end;

function fib(nf:integer):longint;
begin
if (nf=1) or (nf=2) then fib:=1
else fib:=fib(nf-1)+fib(nf-2);
end;

Итерацией:

Рекурсией:

Perevertish;
Var n: longint;
Procedure reverse(n: longint);
begin
write (n

mod 10);
if n div 10 <> 0 then reverse (n div 10)
end;
Begin
writeln(‘Введите натуральное число <=‘, 2 147 483 647);
readln(n);
reverse(n);
writeln; readln
End.

Измените процедуру. Сформируйте число-«перевертыш». Выдайте сообщение, является ли введенное число палиндромом

при прочтении его справа налево. Например: 121, 1230321, 99

и т.п.

Написать рекурсивную функцию для нахождения:
a) n-го

члена прогрессии;
б) суммы n первых членов арифметической прогрессии.

2. Даны первый член и знаменатель геометрической прогрессии. Написать рекурсивную функцию для нахождения:
a) ее n-го члена;
б) суммы n первых членов прогрессии.

а) суммы цифр натурального числа;
б) количества

цифр натурального числа.

4. Написать рекурсивную процедуру для вывода на экран цифр натурального числа в обратном порядке.
5. Написать рекурсивную функцию, определяющую является ли заданное натуральное число простым.

then {“заглушка”}
begin
circle(x,y,r);r1:=trunc(r*k2); {рисование окружности}

r1:=trunc(r*k2) {вычисление радиуса орбиты}
For i:=1 to 4 do
begin
x1:=trunc(x+r1*cos(pi/2*i); { координаты центра }
y1:=trunc(y+r1*sin(pi/2*i); { i-ой окружности }
Picture1(x1,y1,trunc(r*k1),r1,n-1);
end;
end;
end;