Презентация на тему Системы счисления

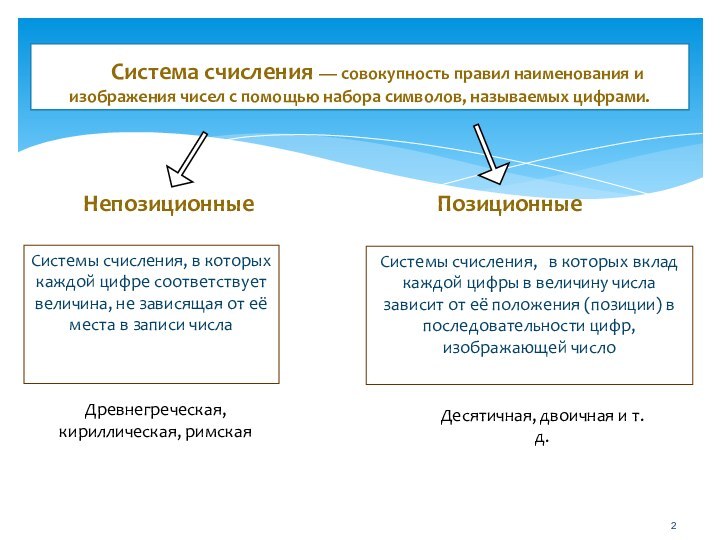
чисел с помощью набора символов, называемых цифрами.
Непозиционные
Позиционные
Системы счисления,

в которых каждой цифре соответствует величина, не зависящая от её места в записи числа

Системы счисления, в которых вклад каждой цифры в величину числа зависит от её положения (позиции) в последовательности цифр, изображающей число

Древнегреческая, кириллическая, римская

Десятичная, двоичная и т.д.

используются 10 чисел – 0,1,2,3,4,5,6,7,8,9.
Позицию, отводимую для цифры числа,

называют разрядом.
Пример:

Для записи десятичных дробей используются отрицательные значения степеней основания!!!

с помощью двух цифр
0 и 1 и называется

двоичным числом.
Каждый разряд(цифру) двоичного числа называют битом.
Например, для двоичного числа 1010101,101 сумма примет следующий вид:

Правило перевода:
Чтобы перевести число из двоичной системы в десятичную систему счисления, нужно двоичное число представить в виде суммы степеней двойки с коэффициентами-цифрами и найти эту сумму.

8, числа выражаются с помощью восьми цифр: 0,1,2,3,4,5,6,7.

Где индекс

«8» у числа 357 обозначается принадлежность к системе счисления.
Выполняя в записанной сумме арифметические действия по правилам десятичной системы, получим, что

систему счисления с основанием 16. Эту систему называют шестнадцатеричной.

Основание = 16
Используются цифры и буквы: 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F.

Выполняя арифметические операции по правилам десятичной системы и учитывая, что А=10, Е=14, получим :

в другую позиционную систему, его последовательно делят на основание

новой системы счисления и каждый раз записывают остаток. Деление продолжается до тех пор, пока целая часть частного не окажется меньше, чем основание системы счисления. Результат формируется путём последовательной записи слева направо цифры старшего разряда и всех записанных остатков в порядке, обратном их получению.

последовательно делят на два и каждый раз записывают остаток:
12310=11110112

на основание системы, а получаемая дробная часть снова умножается

на основание системы. Так продолжается до тех пор, пока не получится нулевая дробная часть .
Полученные целые части произведения записываются в прямой последовательности.

восьмеричную.
Чтобы перевести целое двоичное число в восьмеричное, необходимо его

разбить по три цифры справа налево.
Затем преобразовать каждую группу в восьмеричную цифру.
Если в последней, левой группе окажется меньше трех цифр,то необходимо ее дополнить слева нулями.

ПРИМЕР:

Для быстрого перевода можно воспользоваться таблицей преобразования двоичных групп по три цифры в восьмеричные цифры (Таблица 2.3 – стр. 14)

шестнадцатеричную.
Чтобы перевести целое двоичное число в шестнадцатеричное, необходимо его

разбить по четыре цифры справа налево.
Затем преобразовать каждую группу в шестнадцатеричную цифру.
Если в последней, левой группе окажется меньше четырех цифр,то необходимо ее дополнить слева нулями.

ПРИМЕР:

Для быстрого перевода можно воспользоваться таблицей преобразования двоичных групп по четыре цифры
(Таблица 2.4 – стр. 15)