- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Алгебра и начало анализа. Теорема Безу.
Содержание
- 2. Тема урока:«Теорема Безу»11 класс, физико-математический профиль, МОУ СОШ пгт Ерофей Павлович Амурской области
- 4. Как разложить на множители многочлен х2 -
- 5. Схема Горнера . x3-2x2-6x+4 разделим на
- 6. Значения
- 7. Теорема Безу:Остаток R от деления Р(х) на
- 8. РЕШИТЬ УРАВНЕНИЕ:х4 - x3 - 6x2 - x + 3 = 0.Ответ: -1; 3;
- 9. Скачать презентацию
- 10. Похожие презентации
Тема урока:«Теорема Безу»11 класс, физико-математический профиль, МОУ СОШ пгт Ерофей Павлович Амурской области







Слайд 2
Тема урока:
«Теорема Безу»
11 класс, физико-математический профиль,
МОУ СОШ
пгт Ерофей Павлович Амурской области
Слайд 3
Решить уравнение:
x3-2x2-6x+4=0Проблема:
Возможно ли многочлен третьей степени x3-2x2-6x+4
разложить на множители?
Слайд 4
Как разложить на множители многочлен х2 - 5х
- 6?
х2 - 5х - 6 = (х –
6)(х + 1)Вывод:
Корни трехчлена являются делителями свободного члена.
.
Слайд 5
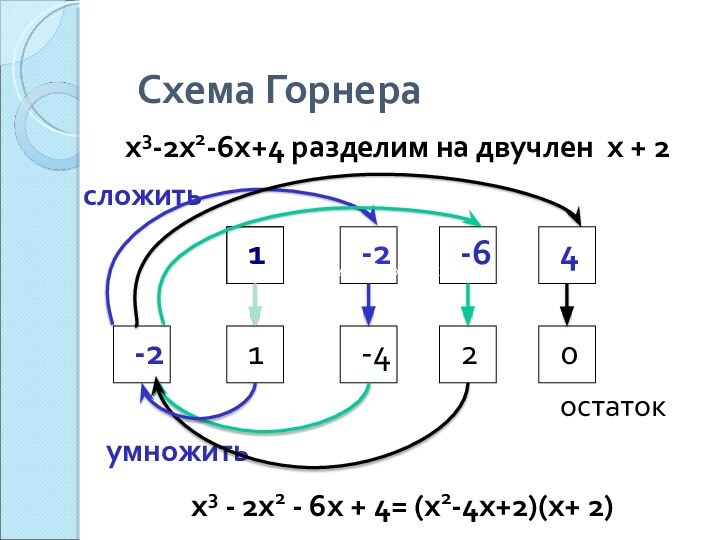
Схема Горнера
.
x3-2x2-6x+4 разделим на двучлен х
+ 2
1
-2
-6
4
1
1
-4
2
0
-2
остаток
умножить
сложить
x3 - 2x2 - 6x +
4= (x2-4x+2)(x+ 2)x3 - 2x2 - 6x + 4= (x2-4x+2)(x+ 2)=
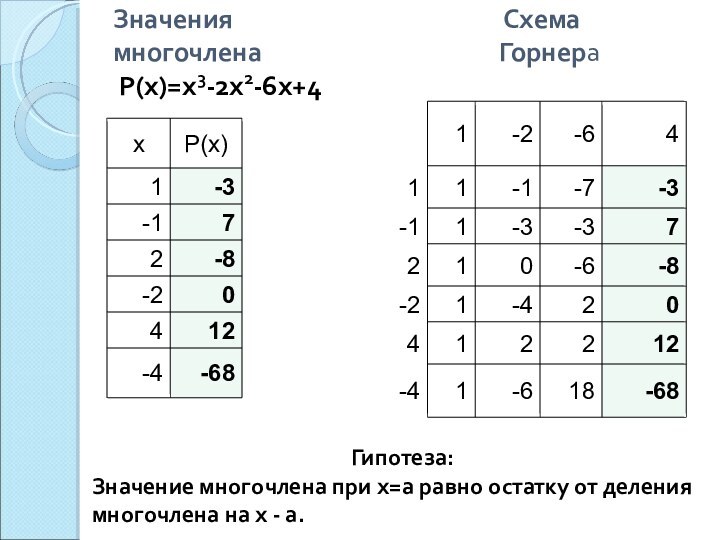
Слайд 6 Значения
Схема многочлена Горнера Р(х)=x3-2x2-6x+4
Гипотеза:
Значение многочлена при х=а равно остатку от деления многочлена на х - а.
Слайд 7
Теорема Безу:
Остаток R от деления Р(х) на двучлен
(x - а) равен Р(а).
Следствие: Для того, чтобы многочлен
Р(х) делился нацело на двучлен (х – а), необходимо и достаточно, чтобы выполнялось равенство Р(а) = 0.О Безу
Этьенн БЕЗУ
Этьенн Безу (1730 - 1783)





























