Презентация на тему Дизъюнктивные нормальные формы (ДНФ). Совершенные дизъюнктивные нормальные формы (СДНФ)

элементарной конъюнкцией.
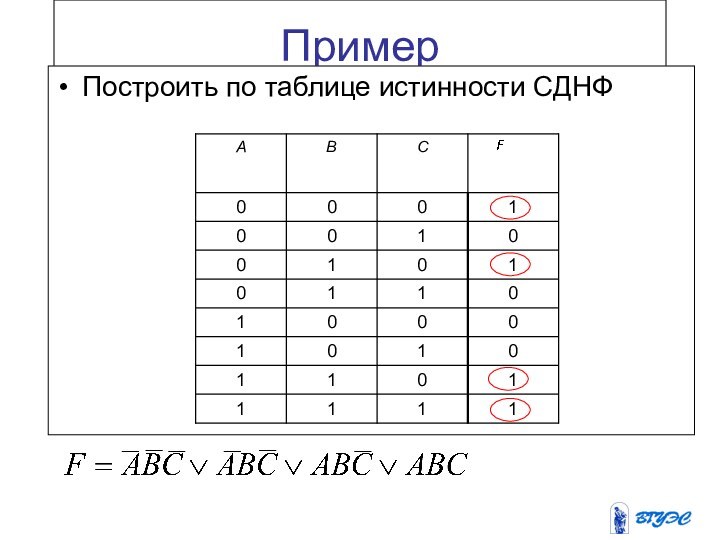
Пример
Определение 2
Высказывание называется дизъюнктивной нормальной формой (ДНФ), если

оно представляет собою дизъюнкцию элементарных конъюнкций.

Общий вид ДНФ:

3. Дизъюнктивные нормальные формы (ДНФ)

к ДНФ
Избавиться от импликации и эквивалентности, используя законы
16), 17)
2)

Донести отрицания до переменных, используя законы Моргана.
3) Раскрыть скобки, используя дистрибутивные законы.
4) Упростить полученное высказывание.

формы (СДНФ)
Определение 1
Пусть

 – некоторое множество логических переменных. Элементарная конъюнкция, в которую входят все логические переменные, называется полной элементарной конъюнкцией относительно множества X .

Пример

все составляющие ее элементарные конъюнкции являются полными.
Примеры


СДНФ

Высказывание, не являющееся тождественно ложным, приводимо к СДНФ.
Правило приведения высказывания к СДНФ
СДНФ содержит столько полных элементарных конъюнкций, сколько единиц в последнем столбце таблице истинности.
Вид каждой полной элементарной определяется соответствующим набором значений переменных, а именно, если переменная принимает значение 0, то над ней в полной элементарной конъюнкцией ставится отрицание, иначе – отрицание не ставится.

Говорит Мегрэ. Есть новости?
- Да, шеф. Поступили сообщения от

инспекторов.
Торранс установил, что если Франсуа был пьян, то либо Этьен убийца, либо Франсуа лжет.
Жуссье считает, что или Этьен убийца, или Франсуа не был пьян и убийство произошло после полуночи.
Инспектор Люка просил передать Вам, что если убийство произошло после полуночи, то либо Этьен убийца, либо Франсуа лжет.
Затем звонила …
- Все. Спасибо. Этого достаточно. – Комиссар положил трубку. Он знал, что трезвый Франсуа никогда не лжет. Теперь он знал все.»
Что знал Мегрэ?

после полуночи»
Тогда получим высказывание








Так как

, то Этьен - убийца