- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Интеграл и его практическое применение
Содержание
- 2. Выполнил:Ершов Николай, ученик 11 класса.Руководитель:Дедовец Надежда Артемовна, учитель математики С. Большой Атлым2012-2013 уч. год
- 3. Цель работы: Расширить область математических знаний. Развивать
- 4. Задачи исследования: - собрать, изучить и систематизировать
- 5. Немного истории -1675 г, опубликовано в 1686
- 6. Евдокс Книдский408 – 355 до н. эАрхимед287
- 7. «Интеграл» придумал Я.Бернулли (1690)«восстанавливать» от латинского integro«целый» от латинского integer
- 8. Исаак Ньютон (1643-1727)Разумом он превосходил род человеческий. Лукреций
- 9. Лейбниц Готфрид Вильгельм (1646-1716) « Общее
- 10. интегральное исчислениенеопределенный интегралопределенныйинтеграл(первообразная)(площадь криволинейной фигуры)И.НьютонГ.Лейбниц
- 11. ДифференцированиеИнтегрированиех(t)v(t)a(t)
- 12. Применение интегралаПлощадь фигурыОбъем тела вращенияРабота электрического зарядаРабота переменной силы МассаПеремещениеДифференциальное уравнениеДавлениеКоличество теплоты
- 13. Задача .Найти объём наклонной треугольной призмы с
- 14. Из эксперимента известно, что скорость размножения
- 16. y“=-ω²y – дифференциальное уравнение гармонических колебаний.ω –
- 17. Уже Архимед успешно находил площади фигур, несмотря
- 18. Скачать презентацию
- 19. Похожие презентации















Слайд 2
Выполнил:
Ершов Николай,
ученик 11 класса.
Руководитель:
Дедовец Надежда Артемовна,
учитель
математики
Слайд 3
Цель работы:
Расширить область математических знаний. Развивать
логическое мышление.
Вывести общие формулы, позволяющие решать задачи интегрирования.
Показать, что интеграл широко применяется в различных сферах жизнедеятельности.
Слайд 4
Задачи исследования:
- собрать, изучить и систематизировать материал
об интеграле;
- рассмотреть, как интеграл используется при решении различных
жизненных ситуаций;- использование интеграла в различных сферах жизнедеятельности.
Объект исследования:
область математики – интегрирование.
Слайд 5
Немного истории
-1675 г, опубликовано в 1686 г
ввел Г.Лейбниц
-
1675 г, Ж Лагранж
5 век до н.э. др.гр. ученый
Демокрит3-4 век до н.э. Архимед ввел метод исчерпывания
Слайд 6
Евдокс Книдский
408 – 355 до н. э
Архимед
287 –
212 до н.э.
Строгое изложение теории интегралов появилось только в
19 веке. Но задачами на вычисление площадей занимались математики Древней Греции.Математики Древней Греции
Слайд 7
«Интеграл» придумал Я.Бернулли (1690)
«восстанавливать» от латинского integro
«целый» от
латинского integer
Слайд 9
Лейбниц Готфрид Вильгельм
(1646-1716)
« Общее искусство знаков
представляет чудесное пособие, так как оно разгружает воображение… Следует
заботиться о том, чтобы обозначения были удобны для открытий. Обозначения коротко выражают и отображают сущность вещей. Тогда поразительным образом сокращается работа мысли.»Лейбниц
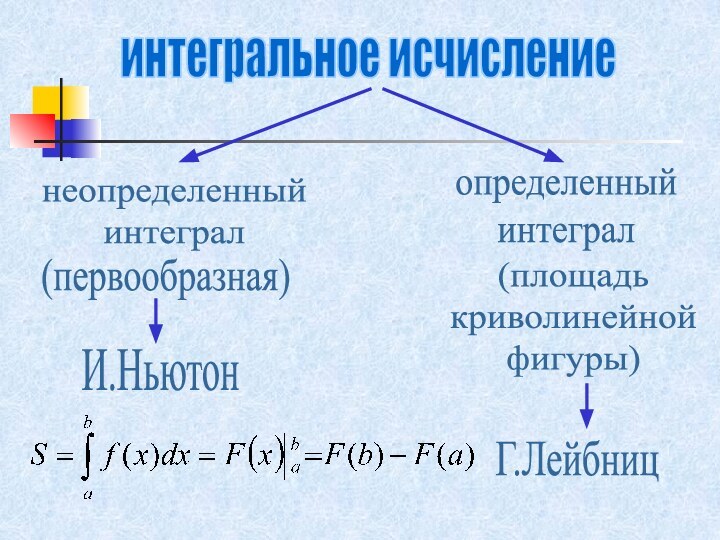
Слайд 10
интегральное исчисление
неопределенный
интеграл
определенный
интеграл
(первообразная)
(площадь
криволинейной
фигуры)
И.Ньютон
Г.Лейбниц
Слайд 12
Применение интеграла
Площадь фигуры
Объем тела вращения
Работа электрического заряда
Работа переменной
силы
Масса
Перемещение
Дифференциальное уравнение
Давление
Количество теплоты
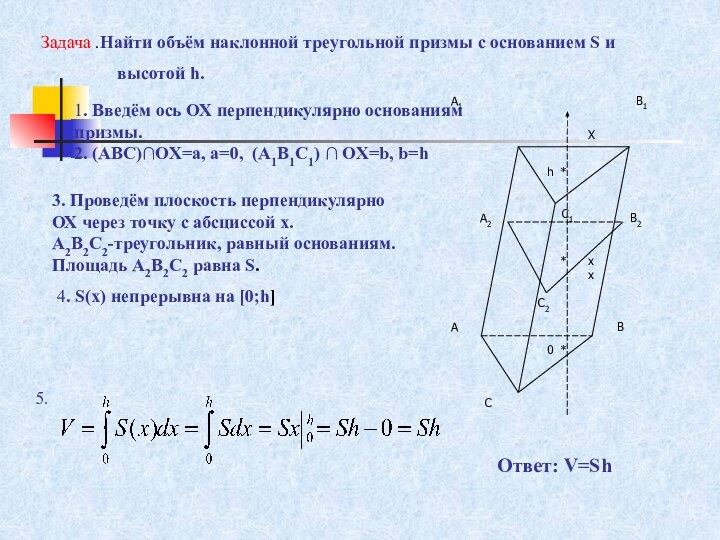
Слайд 13 Задача .Найти объём наклонной треугольной призмы с основанием
S и
высотой h.
1. Введём ось ОХ перпендикулярно основаниям призмы.
2. (АВС)OX=a, a=0, (A1B1C1) OX=b, b=h
3. Проведём плоскость перпендикулярно ОХ через точку с абсциссой х.
А2В2С2-треугольник, равный основаниям.
Площадь А2В2С2 равна S.
Ответ: V=Sh
4. S(x) непрерывна на [0;h]
Слайд 14
Из эксперимента известно, что скорость размножения бактерий
пропорциональна их количеству. За какое время количество бактерий увеличится
в m раз по сравнению с начальным?Решение:
Пусть x(t) – количество бактерий в момент времени t. x(0) = x0. Изменение количества бактерий со временем описывается уравнением
x´(t) = kx(t), k>0, ,
ln|x| = kt+ln|C|,
x=ekteln|C| , x=Cekt - общее решение уравнения.
ЗАДАЧА
Слайд 16
y“=-ω²y – дифференциальное уравнение гармонических колебаний.
ω – заданное
положительное число
y=y‘(x) y“=(y‘(x))‘
Решением являются функции:
Y(x)=Asin(ωx + φ),
гдеA – амплитуда колебания,
ω – частота, φ – начальная фаза.
Графиком гармонических колебаний является синусоида
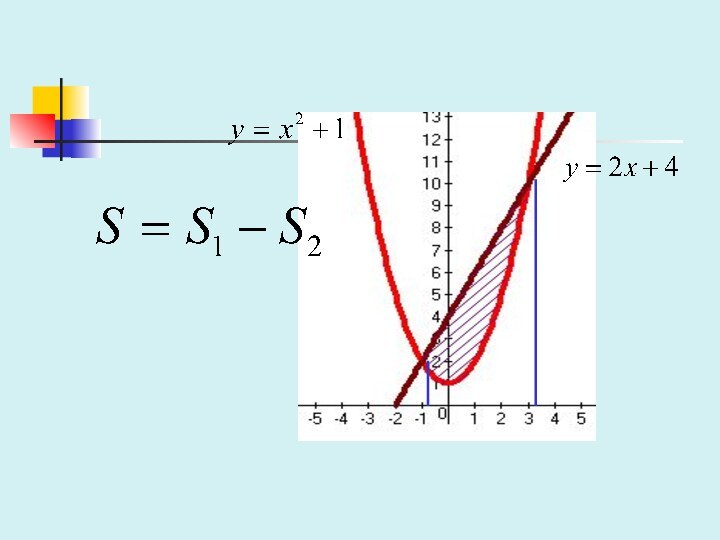
Слайд 17 Уже Архимед успешно находил площади фигур, несмотря на
то, что в математике его времени не было понятия
интегралаНо лишь интегральное исчисление дает общий метод решения задач из различных областей наук.
Недаром даже поэты воспевали интеграл.
Смысл- там, где змеи интеграла
Меж цифр и букв , меж d и f.
Там – власть, там творческие горны!
Пред волей чисел все – рабы.
И солнца путь вершат, покорны
Немым речам и ворожбы.
В.Брюсов.