Презентация на тему Квадратичная функция и её график

= ax2.
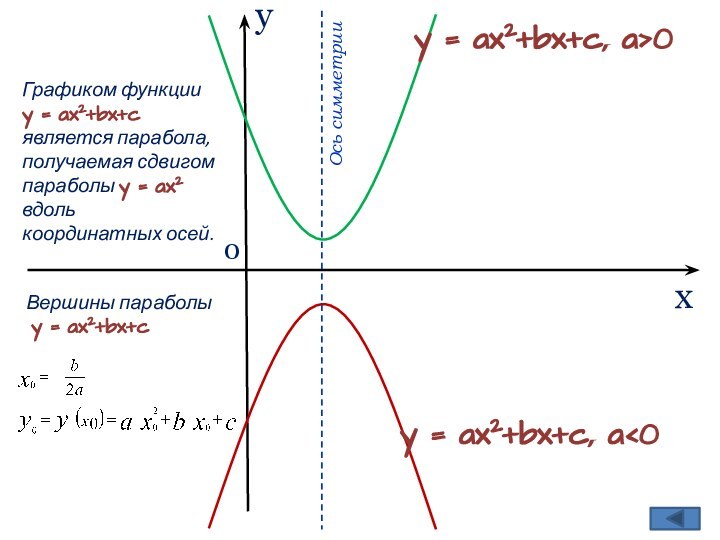
График функции
y = ax2

+ bx + c.
Лабораторно-графическая работа

= ax2, a

2x + 3 и сравнить с графиком функции y

= x2

Построение.
Графиком функции y = x2 – 2x + 3 является парабола, ветви которой направлены вверх.
Составим таблицу значений функции y = x2 – 2x + 3





Построим график функции y = x2 – 2x + 3
Сравним графики y = x2 – 2x + 3 и y = x2
y = x2 – 2x + 3 = x2 – 2x + 1+ 2 = (x – 1)2 + 2
Вывод: Графиком функции y = x2 – 2x + 3 является парабола, получаемая сдвигом параболы y = x2 на единицу вправо и на две единицы вверх.

y = ax2+bx+c является парабола, получаемая сдвигом параболы y

= ax2 вдоль координатных осей.

Вершины параболы
y = ax2+bx+c

Ось симметрии

координаты точек пересечения графика функции с осями координат.
Постройте график

данной функции.
С помощью графика найдите:
множество значений х, на котором функция:
1) возрастает, 2) убывает, 3) принимает положительные значения, 4) принимает отрицательные значения;
значения переменной х, при которых функция принимает наибольшее и наименьшее значение.
Проходит ли график данной функции через точки A(m; n), B(-m; n), C(-m; -n), D(m; -n).