Презентация на тему Некоторые применения теоремы Пифагора

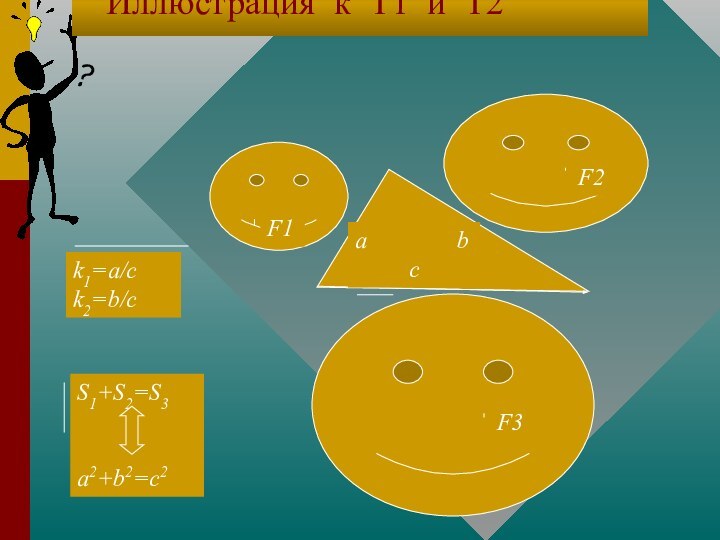
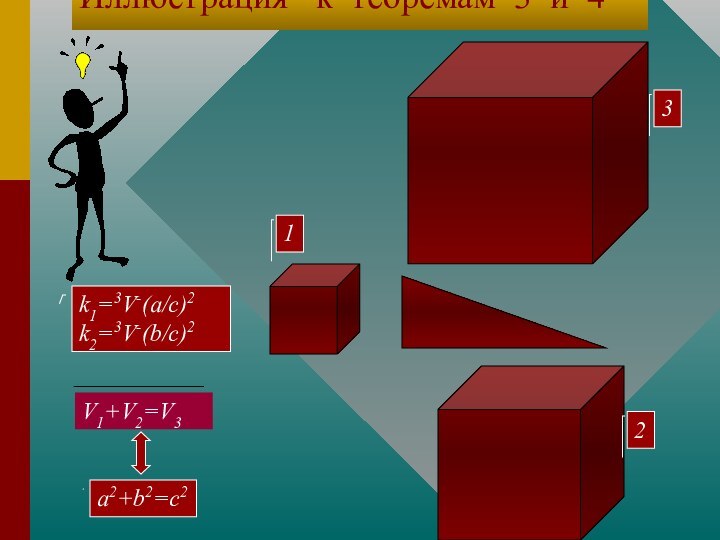
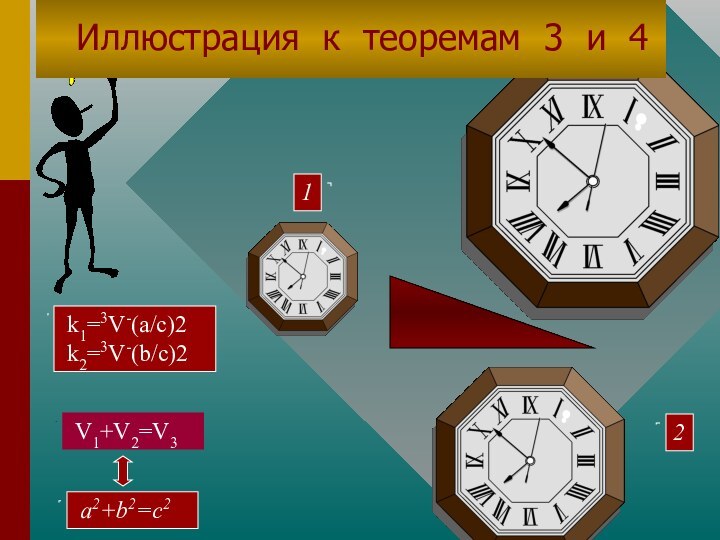
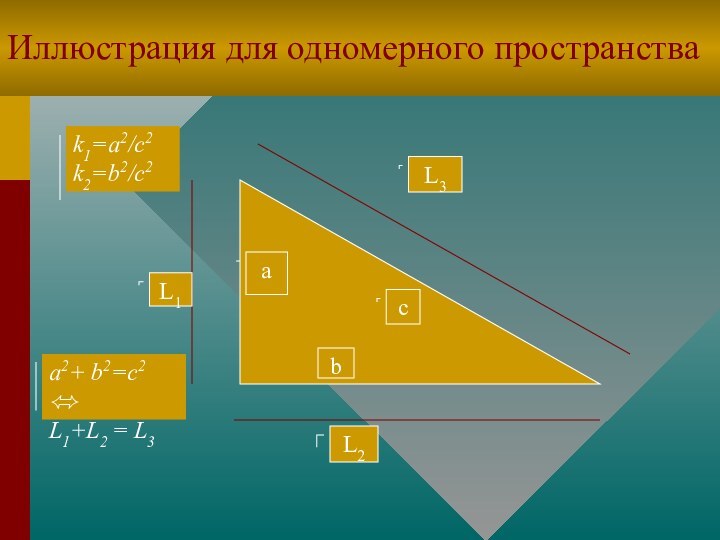
прямоугольного треугольника
ABC соответственно a, b и c ;

sin A = a / c, sin B = b / c ;
фигуры 1, 2, 3, их длины, площади и их объемы
соответственно F1,F2,F3;L1,L2,L3; S1,S2,S3 и V1,V2,V3.

Теорема Пифагора
и подобие фигур

мерного пространства
Будем считать F1 подобной F2 в n

- мерном пространстве с
коэффициентом подобия к , если есть величины W1 и W2
соответственно такие, что W1/W2=kn.
Т1. Если F1 подобна F3, где k=n V¯a2/c2, F2 подобна F3, где
k= n V¯b2/c2, и W1+W2=W3, то a,b и с - стороны прямоугольного треугольника.
Т2. Если F1 подобна F3, где k=n V¯a2/c2, F2 подобна F3, где
k=n V¯ b2/c2, и а,b и с- стороны прямоугольного треугольника,то
W1+W2 = W3.

F1 подобна F3, где k=a/c=sin A, F2 подобна

F3, где k=b/c=sin B, и S1+S2=S3 , то a,b и c- стороны прямоугольного треугольника.

Т2. Если F1 подобна F3, где k=a/c=sin A, F2 подобна F3, где k=b/c=sin B, причем a, b и c- стороны прямоугольного треугольника, то S1+S2=S3.

1 и 2

Из подобия фигур следует равенство :
S1+S2 =S3(a2+b2)/c2 (см.доказательствоТ2).
По

условию S1+S2=S3 , следовательно
(a2+b2)/c2=1 , откуда а2+b2=c2 . Тогда по
обратной теореме Пифагора имеем : a, b и c
есть стороны прямоугольного треугольника.
Теорема доказана.

Т2
Из подобия фигур, отношение площадей

которых равно квадрату коэффициента
подобия, следует : S1= (a2/c2)S3 , S2= (b2/c2)S3.
Тогда S1+S2= (a2/c2) S3+ (b2/c2)S3 =
=(a2/c2+b2/c2)S3=S3(a2+b2)/c2=S3, так как по
теореме Пифагора a2+b2=c2.
Итак , имеем S1+S2=S3. Теорема доказана.

b
c
S1+S2=S3


a2+b2=c2
k1=a/c
k2=b/c

Иллюстрация к Т1 и Т2

Если F1 подобна F3, где k=3V¯(a/c)2, F2 подобна

F3 , где k=3V¯(b/c)2 , и V1+V2=V3 , то a,b и c- стороны прямоугольного треугольника.
Т4. Если F1 подобна F3, где k=3V¯(a/c)2, F2 подобна F3 , где k=3V¯(b/c)2, причем a, b и c - стороны прямоугольного треугольника, то верно V1+V2=V3.

Отношение объемов подобных фигур равно кубу коэффициента подобия, поэтому

V1=(а2/c2)V3 и V2=(b2/c2)V3 , откуда V1+V2=V3(a2+b2)/c2. (1)
Т3.По условию V1+V2=V3 ,тогда из равенства(1)
следует a2+b2=c2 и то,что a,b и c - cтороны
прямоугольного треугольника.
Т4. По условию a,b и c-стороны прямоугольного
треугольника, т.е. a2+b2=c2,тогда из равенства
(1) следует, что V1+V2=V3. Теоремы доказаны.

Доказательство Т3 и Т4

теоремам 3 и 4

F1 подобна F3, где к=а2/с2, F2 подобна F3 ,
где

к=b2/c2, и L1+L2=L3 , то a,b и с - стороны
прямоугольного треугольника .
Т6. Если F1 подобна F3, где к=а2/с2, F2 подобна F3 ,
где к=b2/c2, и а,b и с - стороны прямоугольного
треугольника , то L1+L2=L3 .