Презентация на тему Симметрия фигур

плоскости α в пространстве (относительно прямой а на плоскости),

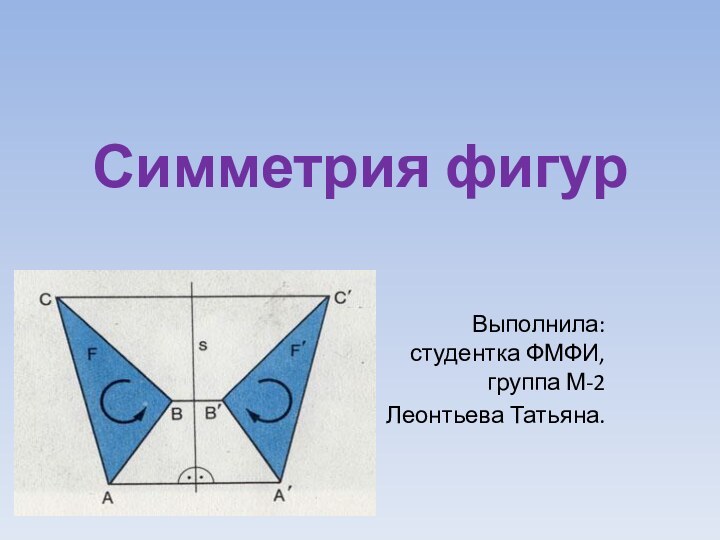
— преобразование пространства (плоскости), при котором каждая точка М переходит в точку M' такую, что отрезок MM' перпендикулярен плоскости α (прямой а) и делится ею пополам. Плоскость α (прямая а) называется плоскостью (осью) симметрии.

М

M'

а

Ф, характеризующее некоторую правильность формы Ф, неизменность её при

действии движений и отражений. Точнее, фигура Ф обладает симметрией, если существует нетождественное ортогональное преобразование, переводящее эту фигуру в себя.

с самой собой, является группой, называемой группой симметрии этой

фигуры (иногда сами эти преобразования называются симметриями).

себя при отражении, симметрична относительно прямой — оси С.

(рис. 1); здесь группа симметрии состоит из двух элементов.

Рис. 1. Плоская фигура, симметричная относительно прямой АВ; точка М преобразуется в М’ при отражении (зеркальном) относительно АВ.

такова, что повороты относительно какой-либо точки О на угол

360°/n, n — целое число ≥ 2, переводят её в себя, то Ф обладает С. n-го порядка относительно точки О — центра С. Примером таких фигур являются правильные многоугольники (рис. 2); группа симметрии здесь —циклическая группа n-го порядка.

Рис. 2. Звездчатый правильный многоугольник, обладающий симметрией восьмого порядка относительно своего центра.

порожденной отражениями, являются центральная С., зеркальная С., осевая С.

и С. переноса.

фигура Ф совмещается сама с собой после последовательных отражений

от трёх взаимно перпендикулярных плоскостей, другими словами, точка О — середина отрезка, соединяющего симметричные точки Ф (рис. 3)

Рис. 3. Куб, имеющий прямую AB осью симметрии третьего порядка, прямую CD — осью симметрии четвёртого порядка, точку О — центром симметрии. Точки М и M' куба симметричны как относительно осей AB и CD, так и относительно центра О.

относительно прямой n-го порядка, фигура накладывается на себя вращением

вокруг некоторой прямой (оси С.)на угол 360°/n( рис. 3а). Фигура, накладывающаяся на себя последовательным вращением на угол 360°/2k вокруг прямой AB и отражением в плоскости, перпендикулярной к ней, имеет зеркально-осевую С( рис.4).

Рис. 4 Многогранник, обладающий зеркально-осевой симметрией; прямая AB — зеркально-поворотная ось четвёртого порядка.

Рис.3а

себя переносом вдоль некоторой прямой (оси переноса) на какой-либо

отрезок (рис.5)

Рис. 5. Фигуры, обладающие симметрией переноса: верхняя фигура имеет также бесконечное множество вертикальных осей симметрии (второго порядка), т. е. плоскостей отражения

роль при исследовании кристаллических решёток.