Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Чистая приведенная стоимость

Содержание

Чистая приведенная стоимостьВо-вторых, необходимо определить соответствующие альтернативные издержки инвестирования. В-третьих, следует использовать данные альтернативных издержек для дисконтирования будущих потоков денежных средств, производимых проектом Клякса.
Чистая приведенная стоимостьФинансовый менеджер компании Конус решили вложить 10 млн руб. в Чистая приведенная стоимостьВо-вторых, необходимо определить соответствующие альтернативные издержки инвестирования. В-третьих, следует использовать Чистая приведенная стоимостьСумма дисконтированных денежных потоков, генерируемых проектом Клякса в будущем, называется Чистая приведенная стоимостьВ-четвертых, нужно рассчитать чистую приведенную стоимость (NPV), получаемую посредством вычитания Чистая приведенная стоимостьОднако слушатель, к сожалению, часто не воспринимает на веру те Чистая приведенная стоимостьПопробуем доказать ошибочность такого подхода у нашего слушателя. Давайте посмотрим, Чистая приведенная стоимостьВ данный момент общая рыночная стоимость компании Конус (цена одной Чистая приведенная стоимостьСледовательно, стоимость других активов и возможностей компании Конус должна равняться Чистая приведенная стоимость Определим приведенную стоимость нового проекта. Тогда выбор будет выглядеть следующим образом: Чистая приведенная стоимостьОчевидно, проект Клякса стоит принять, если его приведенная стоимость больше Чистая приведенная стоимостьНа этот вопрос можно ответить так: Чистая приведенная стоимостьИнвесторы могут предположить, какие дивиденды способна выплачивать фирма Клякса, и Чистая приведенная стоимостьТак как проект Клякса составляет все активы фирмы Клякса, мы Чистая приведенная стоимостьКроме того, ставка, по которой инвесторы могут дисконтировать дивиденды фирмы Чистая приведенная стоимостьКонечно, пример фирмы Клякса - чисто гипотетический. Но если проект Чистая приведенная стоимостьМы знаем, что другие активы компании Конус, рассматриваемые отдельно, стоят Чистая приведенная стоимостьМожно уверенно сказать, что определяя приведенную стоимость проекта Клякса, мы Чистая приведенная стоимостьУ нашего слушателя появляется новый вопрос: «Можно ли уточнить, откуда Чистая приведенная стоимостьЭту тему мы уже обсуждали, но вновь рассмотрим суть этой Чистая приведенная стоимостьСтавка дисконта представляет собой альтернативные издержки инвестирования в проект, а 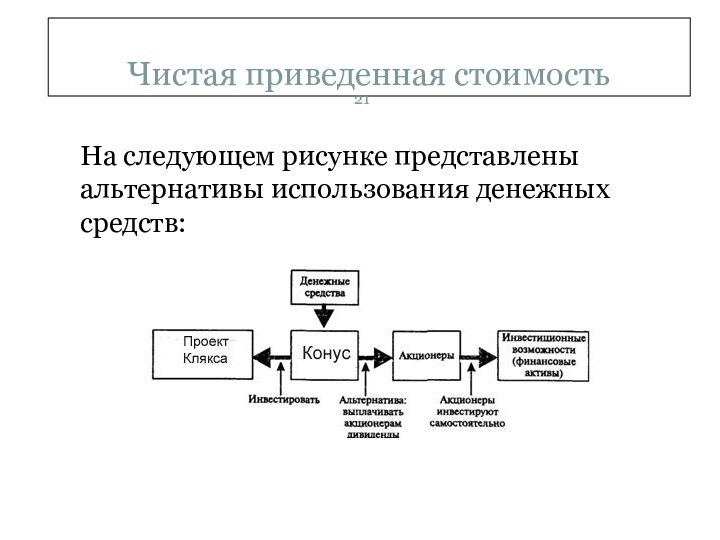Чистая приведенная стоимостьНа следующем рисунке представлены альтернативы использования денежных средств: Чистая приведенная стоимостьНа этом рисунке показан выбор между двумя возможными вариантами. Альтернативные Чистая приведенная стоимостьКогда мы дисконтируем потоки денежных средств по ожидаемой норме доходности Чистая приведенная стоимостьЕще раз обратим внимание слушателя, что идея альтернативных издержек имеет Чистая приведенная стоимостьВ общем случае мы должны выявить активы, риск которых эквивалентен Чистая приведенная стоимостьПредставляется, что теперь любознательный слушатель убедился в корректности правила чистой Чистая приведенная стоимостьСейчас мы предлагаем четыре наиболее известных критерия, альтернативных правилу чистой Чистая приведенная стоимостьПринимая во внимание эти альтернативные критерии, слушателям стоит напомнить следующие Чистая приведенная стоимостьПервое правило чистой приведенной стоимости предполагает, что стоимость рубля сегодня Чистая приведенная стоимостьВторое правило - чистая приведенная стоимость зависит исключительно от прогнозируемых Чистая приведенная стоимостьЛюбое правило инвестирования, на которое влияют предпочтения менеджеров, выбранные компанией Чистая приведенная стоимостьТретье правило — поскольку приведенные стоимости измеряются в текущих рублях, Чистая приведенная стоимостьЭто свойство аддитивности стоимостей имеет важное практическое значение. 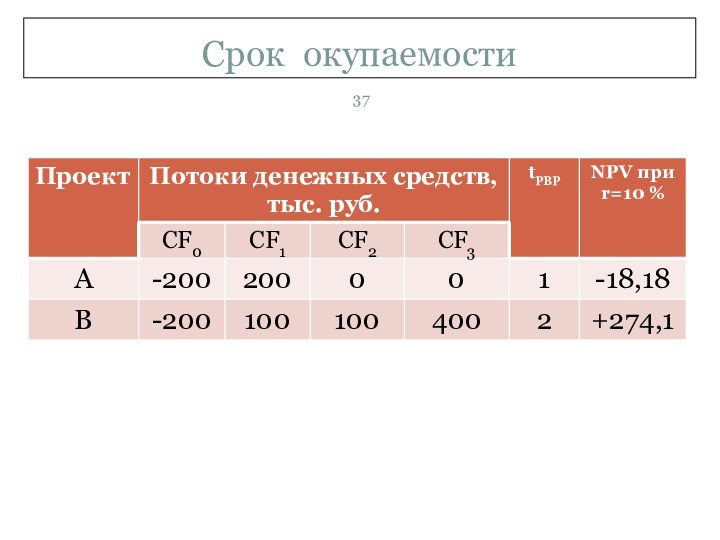Предположим, проект Чистая приведенная стоимостьПоэтому маловероятно, что аналитик ошибется в оценке плохого проекта В Чистая приведенная стоимостьИ если аналитик будет невнимателен, то может впасть в заблуждение, Срок окупаемостиКомпании часто требуют, чтобы первоначальные инвестиции в какой-либо проект окупались в Срок окупаемости Срок окупаемостиПервоначальные инвестиции в проект А составляют 200 тыс. руб. (I0= -200 Срок окупаемостиПроект В также требует первоначальных инвестиций в размере 200 тыс. 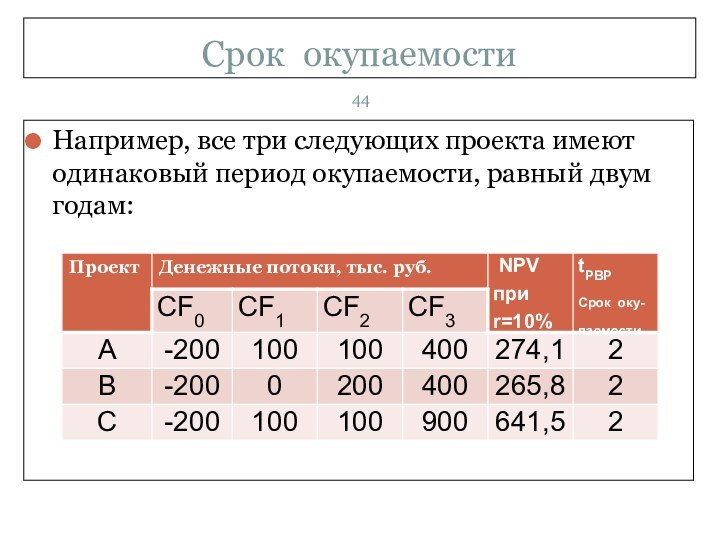руб., Срок окупаемостиТеперь давайте посмотрим, как быстро окупятся первоначальные инвестиции по каждому из Срок окупаемостиЕсли компания придерживается правила, что период окупаемости должен быть не больше Срок окупаемости Следовательно, вне зависимости от выбора периода окупаемости правило окупаемости Срок окупаемости Причина расхождения в результатах состоит в том, что в соответствии Срок окупаемостиНапример, все три следующих проекта имеют одинаковый период окупаемости, равный двум годам: Срок окупаемостиСогласно правилу окупаемости, все эти три проекта одинаково привлекательны. Но проект Срок окупаемостиРуководствуясь правилом окупаемости, компания должна определить соответствующий период окупаемости. Если компания Срок окупаемостиЕсли в среднем периоды окупаемости достаточно продолжительные, некоторые проекты, принятые корпорацией, Срок окупаемостиМногие фирмы, которые действуют в соответствии с принципом окупаемости, выбирают продолжительность Срок окупаемостиЕсть возможность поступать более обоснованно. Если вам известна типичная схема потоков Срок окупаемостиЕсли в среднем инвестиции осуществляются равномерно в течение жизни проекта, оптимальный Срок окупаемостиОднако этот принцип Срок окупаемостиНекоторые финансовые менеджеры, прежде чем определять период окупаемости, дисконтируют потоки денежных Срок окупаемостиЭта модификация принципа окупаемости позволяет избежать ошибок, связанных с единообразной оценкой Срок окупаемостиПредположим, есть два взаимоисключающих инвестиционных проекта, А и В. Каждый проект Срок окупаемостиПотоки денежных средств для проекта А равны 600 тыс. руб. и Срок окупаемостиПроект В очевидно привлекательнее проекта А, исходя из чистой приведенной стоимости. Срок окупаемостиЕжегодное поступление денег по проекту А больше, чем по проекту В, Срок окупаемостиПериод окупаемости проекта А немногим меньше 5 лет, так как приведенная Срок окупаемостиДисконтированная окупаемость служит лучшим критерием, чем не дисконтированная. Она учитывает, что Срок окупаемостиЭтот показатель полезный, но не слишком. Принцип дисконтированной окупаемости все же Бухгалтерская норма рентабельностиНекоторые компании оценивают инвестиционные проекты по бухгалтерской норме рентабельности. Для Бухгалтерская норма рентабельностиЗатем этот коэффициент сравнивается с бухгалтерской нормой рентабельности фирмы в Бухгалтерская норма рентабельностиПример. В следующей таблице представлен прогнозный отчет о прибыли Бухгалтерская норма рентабельностиСредняя чистая прибыль составит: Pav=(50000+40000+30000)/3=40 000 руб. 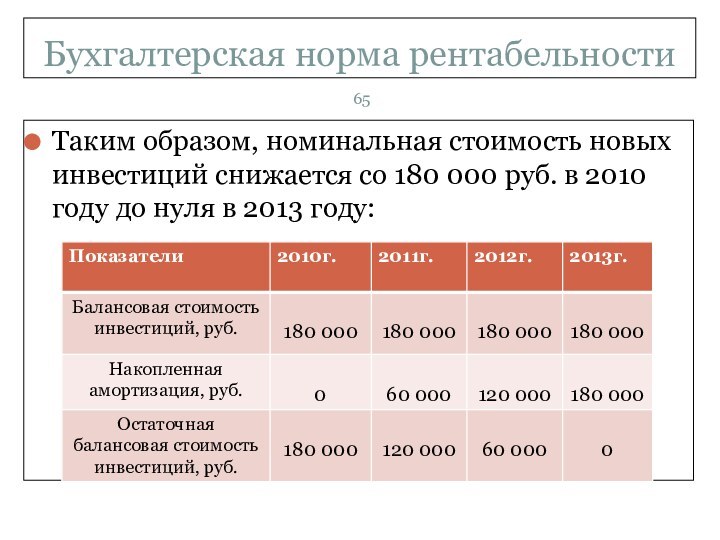Для упрощения Бухгалтерская норма рентабельностиТаким образом, номинальная стоимость новых инвестиций снижается со 180 000 Бухгалтерская норма рентабельностиСредняя остаточная балансовая стоимость инвестиций равна: Бухгалтерская норма рентабельностиДанный показатель эффективности инвестиционного проекта имеет несколько серьезных недостатков. Первый: Бухгалтерская норма рентабельностиЕсли в правиле окупаемости инвестиций не принимаются во внимание более Бухгалтерская норма рентабельностиВ следующей таблице приводятся данные по трем проектам. Проекты В Чистая приведенная стоимость Бухгалтерская норма рентабельностиВо-вторых, показатель средней прибыли в расчете на балансовую стоимость инвестиций Бухгалтерская норма рентабельностиНапример, бухгалтеры относят некоторые направления оттоков денежных средств к капитальным Бухгалтерская норма рентабельностиВозмещение капитальных затрат происходит согласно произвольно выбранной бухгалтером схеме. Затем Бухгалтерская норма рентабельностиПоэтому средняя прибыль в расчете на балансовую стоимость активов зависит Бухгалтерская норма рентабельностиОднако решения бухгалтера не в состоянии воздействовать на величину потоков Бухгалтерская норма рентабельностиКомпания, использующая показатель средней прибыли в расчете на балансовую стоимость Бухгалтерская норма рентабельностиВ таких случаях компании с высокими нормами рентабельности своего уже Бухгалтерская норма рентабельностиПравило окупаемости плохой критерий. Правило средней прибыли в расчете на Внутренняя норма доходностиСледующим критерием оценки эффективности инвестиционного проекта является показатель внутренней нормы Внутренняя норма доходностиИ когда мы будем анализировать достоинства и недостатки этого показателя, Внутренняя норма доходностиПрежде всего, обратим внимание нашего слушателя на возможность выражения чистой Внутренняя норма доходности Данное утверждение, если его правильно интерпретировать, безусловно, корректно. Однако Внутренняя норма доходностиПри определении нормы доходности (rN) инвестиций, которые приносят единственный поток Внутренняя норма доходностиИли же мы можем записать формулу чистой приведенной стоимости инвестиций Внутренняя норма доходностигде I – инвестированный капитал в период 0, руб. Внутренняя норма доходностиКонечно, CF1 — это поступления, I— требуемые инвестиции, и, таким Внутренняя норма доходностиК сожалению, нет вполне удовлетворительного способа найти точную норму доходности Внутренняя норма доходностиПоказатель внутренней нормы доходности часто используется при оценке инвестиционных проектов Внутренняя норма доходностиНапомним слушателям еще раз, что внутренняя норма доходности (IRR) определяется Внутренняя норма доходностиЭто означает, что для определения IRR инвестиционного проекта продолжительностью t Внутренняя норма доходностиИскомая ставка дисконтирования и будет внутренней нормой доходности инвестиционного проекта. Внутренняя норма доходностиПример. Инвестору предлагается купить финансовый инструмент, стоимость которого равна 7704 Внутренняя норма доходностиТаблица 1. Денежные потоки, генерируемые финансовым инструментам по годам Внутренняя норма доходностиЧтобы определить доходность инвестированного капитала, мы должны перебрать разные ставки Внутренняя норма доходностиТаблица 2. Расчет приведенной стоимости будущих денежных потоков Внутренняя норма доходностиПолученный результат показывает, что при ставке дисконтирования 10 % не Внутренняя норма доходностиРасчет текущей стоимости будущих денежных потоков при этой ставке дисконтирования Внутренняя норма доходностиПри дисконтной ставке, равной 14 %, вновь не выполняется условие Внутренняя норма доходностиПримем ставку дисконтирования равной 12%. В этом случае сегодняшняя стоимость Внутренняя норма доходности На данном рисунке представлена зависимость показателя NPV от ставки Внутренняя норма доходностиИз этого рисунка видно, что ставка дисконта на уровне 12 Внутренняя норма доходностиСогласно правилу внутренней нормы доходности инвестиционный проект следует принять, если Внутренняя норма доходностиЕсли альтернативные издержки меньше внутренней нормы доходности, равной 12 %, Внутренняя норма доходностиЕсли альтернативные издержки равны внутренней норме доходности, проект имеет нулевую Внутренняя норма доходностиСледовательно, когда мы сравниваем альтернативные издержки инвестирования с внутренней нормой Внутренняя норма доходностиЭто верно применительно не только к нашему примеру. Вывод, сделанный Внутренняя норма доходностиОбратим внимание слушателя на очень важное замечание по показателю IRR. Внутренняя норма доходностиВнутренняя норма доходности является измерителем рентабельности, которая зависит исключительно от Внутренняя норма доходностиВеличина альтернативных издержек устанавливается на рынках капиталов. Они представляют собой Внутренняя норма доходностиМногие финансовые менеджеры предпочитают в качестве критерия использовать не чистую Внутренняя норма доходностиЗаблуждение 1. Не у всех денежных потоков чистая приведенная стоимость Внутренняя норма доходностиВнутренняя норма доходности каждого из проектов составляет 50%,что видно из Внутренняя норма доходностиОзначает ли это, что оба проекта одинаково привлекательны? Ясно, что Внутренняя норма доходностиКогда мы предоставляем кредит, мы хотим получить высокую норму доходности; Внутренняя норма доходностиДавайте для наших проектов увеличим ставку дисконта до 25 % Внутренняя норма доходностиТаким образом, показатель NPV для проекта А снизился с 4 Внутренняя норма доходностиРассмотрим еще один проект С, для которого денежные потоки представлены в следующей таблице: Внутренняя норма доходностиРасчеты показывают, чистая приведенная стоимость проекта С равна нулю при Внутренняя норма доходностиВ какой-то степени он аналогичен также предоставлению займа, поскольку в Внутренняя норма доходностиПоказатель NPV проекта С растёт с ростом ставки дисконта. Если Внутренняя норма доходностиПри ставке дисконтирования 25% показатель NPV для проекта С будет Внутренняя норма доходностиЗаблуждение 2. Иногда слушатель предполагает, что показатель IRR для проекта Внутренняя норма доходностиРассмотрим, например, проект Лямбда. Затраты по нему составляют 10 000 Внутренняя норма доходностиСуществуют два значения ставки дисконта, при которых чистая приведенная стоимость Внутренняя норма доходностиТаким образом, внутренняя норма доходности инвестиций составляет 20% и 500%. Внутренняя норма доходностиЗаблуждение 3. Фирмам часто приходится выбирать один из нескольких альтернативных Внутренняя норма доходностиРассмотрим проекты D и E: Внутренняя норма доходностиОба проекта представляют собой хорошие варианты инвестирования, но проект D Внутренняя норма доходностиЕсли инвестор будет руководствоваться методом внутренней нормы доходности, его удовлетворит Внутренняя норма доходностиВ таких случаях рекомендуется использовать метод внутренней нормы доходности для Внутренняя норма доходностиВо-вторых, инвестор решает стоит ли инвестировать дополнительно 10 000 дол. Внутренняя норма доходностиВнутренняя норма доходности дополнительных инвестиций равна 30%, что также значительно Внутренняя норма доходностиБез рассмотрения приростных вложений внутренняя норма доходности не может служить Внутренняя норма доходностиДля иллюстрации такого подхода рассмотрим пример, в котором денежные потоки Чистая приведенная стоимость NPV, долл. Чистая приведенная стоимостьПроект А имеет более высокую внутреннюю норму доходности, но у Чистая приведенная стоимость NPV, долл. Чистая приведенная стоимостьЧёрная линия обозначает чистую приведенную стоимость проекта А при различных Чистая приведенная стоимость NPV, долл. Чистая приведенная стоимостьАналогично, красная линия обозначает чистую приведенную стоимость проекта Б при Чистая приведенная стоимостьПричина, по которой метод внутренней нормы доходности ведёт к ошибочным Чистая приведенная стоимостьЕсли посмотреть на внутренние нормы доходности двух проектов, то заметим, Чистая приведенная стоимостьВ рассматриваемом примере альтернативные издержки равны не 20%, а 10%. Чистая приведенная стоимостьЕсли фирма сталкивается с ограничениями на капитал, либо объективные, либо Чистая приведенная стоимостьС помощью метода внутренней нормы доходности такой пакет определить невозможно. Чистая приведенная стоимостьВнутренняя норма доходности дополнительных инвестиций в проект Б равна 15,6%. 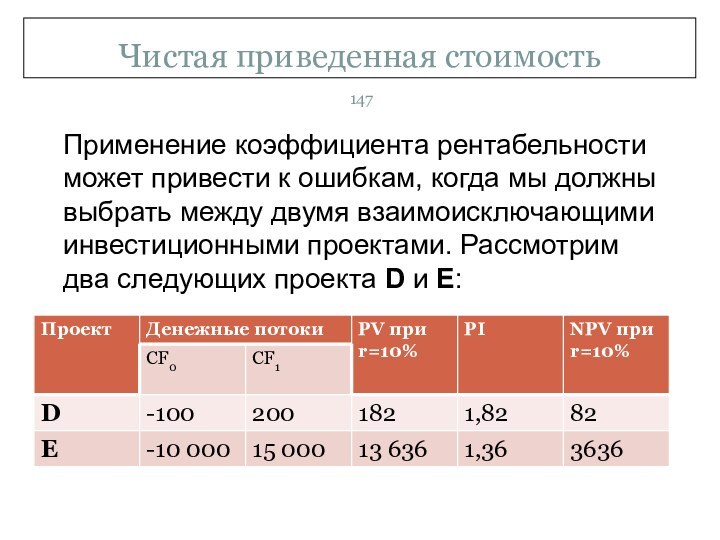Чистая приведенная стоимостьПрименение коэффициента рентабельности может привести к ошибкам, когда мы должны Чистая приведенная стоимостьКоэффициент рентабельности инвестиций указывает, что оба проекта хороши. Но если Чистая приведенная стоимостьКак и в случае с внутренней нормой доходности, инвестор всегда Чистая приведенная стоимостьВ этом случае рентабельность дополнительных инвестиций будет равна 1,36, и, Чистая приведенная стоимостьМы рассмотрели несколько критериев оценки эффективности инвестиционных проектов. Для большинства Чистая приведенная стоимостьАнализ чувствительности - систематический способ анализа, при котором определяются факторы, Учет риска при оценке капиталовложенийa) вычисляются числовые оценки зависимых переменных (NPV или Учет риска при оценке капиталовложенийПример. Денежные потоки, получаемые в результате реализации проекта Учет риска при оценке капиталовложений Учет риска при оценке капиталовложенийОпределим экономические показатели, получаемые при реализации проекта.1. Валовая Учет риска при оценке капиталовложений3. Налог на прибыль = (ставка налога на Учет риска при оценке капиталовложений6. 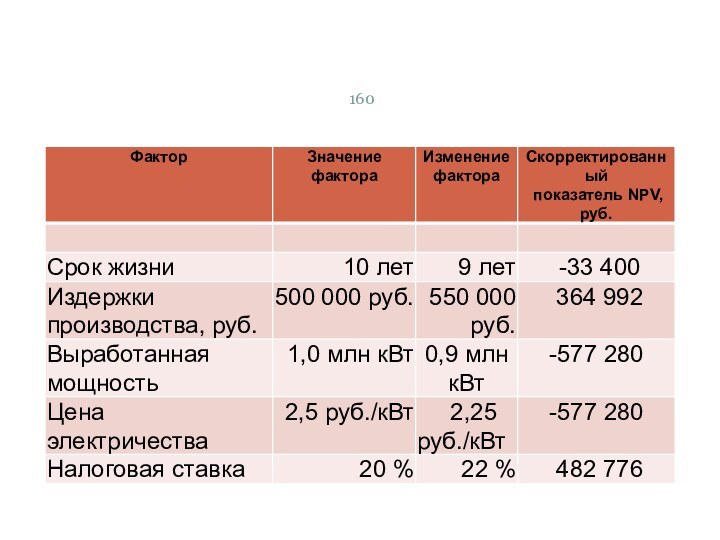Приведенная величина будущих денежных потоков определяется по Учет риска при оценке капиталовложенийОценим чувствительность показателя NPV к ошибке в 10 Учет риска при оценке капиталовложений Таблица 2 Учет риска при оценке капиталовложенийИз данных табл. 2 можно сделать вывод, что Учет риска при оценке капиталовложенийПри дискретном распределении вероятности значений денежных потоков математическое Учет риска при оценке капиталовложенийКоэффициент вариации CV вероятностного распределения определяется следующим образом: Учет риска при оценке капиталовложенийСреднеквадратическое отклонение служит мерой неопределенности величины денежного потока Учет риска при оценке капиталовложенийПример 8.17. Предположим, что среднеквадратическое отклонение наличного потока Учет риска при оценке капиталовложенийТогда показатель CV для А равен 0,5 или Учет риска при оценке капиталовложений Учет риска при оценке капиталовложений Чистая приведенная стоимость Чистая приведенная стоимость Чистая приведенная стоимость Чистая приведенная стоимость Чистая приведенная стоимость Чистая приведенная стоимость Чистая приведенная стоимость Чистая приведенная стоимость Чистая приведенная стоимость Чистая приведенная стоимость Чистая приведенная стоимость Чистая приведенная стоимость Чистая приведенная стоимость Чистая приведенная стоимость Чистая приведенная стоимость Чистая приведенная стоимость Чистая приведенная стоимость Чистая приведенная стоимость Чистая приведенная стоимость Чистая приведенная стоимость Чистая приведенная стоимость Чистая приведенная стоимость Чистая приведенная стоимость Чистая приведенная стоимость Чистая приведенная стоимость Чистая приведенная стоимость Чистая приведенная стоимость Чистая приведенная стоимость Чистая приведенная стоимость Чистая приведенная стоимость Чистая приведенная стоимость Чистая приведенная стоимость Чистая приведенная стоимость Чистая приведенная стоимость Чистая приведенная стоимость Чистая приведенная стоимость Чистая приведенная стоимость Чистая приведенная стоимость Чистая приведенная стоимость Чистая приведенная стоимость Чистая приведенная стоимость Чистая приведенная стоимость Чистая приведенная стоимость Чистая приведенная стоимость Чистая приведенная стоимость Чистая приведенная стоимость Чистая приведенная стоимость Чистая приведенная стоимость Чистая приведенная стоимость Чистая приведенная стоимость Чистая приведенная стоимость Чистая приведенная стоимость Чистая приведенная стоимость Чистая приведенная стоимость Чистая приведенная стоимость Чистая приведенная стоимость Чистая приведенная стоимость Чистая приведенная стоимость Чистая приведенная стоимость Чистая приведенная стоимость Чистая приведенная стоимость Чистая приведенная стоимость Чистая приведенная стоимость Чистая приведенная стоимость Чистая приведенная стоимость Чистая приведенная стоимость Чистая приведенная стоимость Чистая приведенная стоимость Чистая приведенная стоимость Чистая приведенная стоимость Чистая приведенная стоимость Чистая приведенная стоимость Чистая приведенная стоимость
Слайды презентации

Слайд 2 Чистая приведенная стоимость
Во-вторых, необходимо определить соответствующие альтернативные издержки

Чистая приведенная стоимостьВо-вторых, необходимо определить соответствующие альтернативные издержки инвестирования. В-третьих, следует

инвестирования.
В-третьих, следует использовать данные альтернативных издержек для дисконтирования

будущих потоков денежных средств, производимых проектом Клякса.

Слайд 3 Чистая приведенная стоимость

Сумма дисконтированных денежных потоков, генерируемых проектом

Чистая приведенная стоимостьСумма дисконтированных денежных потоков, генерируемых проектом Клякса в будущем,

Клякса в будущем, называется приведенной стоимостью этих потоков.

Слайд 4 Чистая приведенная стоимость
В-четвертых, нужно рассчитать чистую приведенную стоимость

Чистая приведенная стоимостьВ-четвертых, нужно рассчитать чистую приведенную стоимость (NPV), получаемую посредством

(NPV), получаемую посредством вычитания 10 млн руб. инвестиций из

суммы приведенной стоимости будущих денежных потоков, генерируемых проектом. Если чистая приведенная стоимость будет больше нуля, следует инвестировать 10 млн руб. в проект Клякса.

Слайд 5 Чистая приведенная стоимость
Однако слушатель, к сожалению, часто не

Чистая приведенная стоимостьОднако слушатель, к сожалению, часто не воспринимает на веру

воспринимает на веру те выше указанные шаги, которые рекомендуется

выполнить при оценке инвестиционного проекта, поскольку он не считает показатель чистой приведенной стоимости достаточно точным показателем.

Слайд 6 Чистая приведенная стоимость
Попробуем доказать ошибочность такого подхода у

Чистая приведенная стоимостьПопробуем доказать ошибочность такого подхода у нашего слушателя. Давайте

нашего слушателя.
Давайте посмотрим, что будет лучше для

акционеров копании Конус. Они хотят, чтобы финансовый менеджер повысил стоимость акций Конус, насколько это возможно.

Слайд 7 Чистая приведенная стоимость
В данный момент общая рыночная стоимость

Чистая приведенная стоимостьВ данный момент общая рыночная стоимость компании Конус (цена

компании Конус (цена одной акции, умноженная на количество акций

в обращении) составляет 100 млн руб. Сюда же входит 10 млн руб., которые планируется инвестировать в проект Клякса.

Слайд 8 Чистая приведенная стоимость
Следовательно, стоимость других активов и возможностей

Чистая приведенная стоимостьСледовательно, стоимость других активов и возможностей компании Конус должна

компании Конус должна равняться 90 млн руб. Финансовому менеджеру

нужно решить, что будет лучше: сохранить 10 млн руб. и отказаться от проекта Клякса или же потратить их и принять этот проект.

Слайд 9 Чистая приведенная стоимость
Определим приведенную стоимость нового проекта.

Чистая приведенная стоимость Определим приведенную стоимость нового проекта. Тогда выбор будет выглядеть следующим образом:

Тогда выбор будет выглядеть следующим образом:


Слайд 10 Чистая приведенная стоимость
Очевидно, проект Клякса стоит принять, если

Чистая приведенная стоимостьОчевидно, проект Клякса стоит принять, если его приведенная стоимость

его приведенная стоимость больше 10 млн руб., т.е. его

показатель NPV > 0.
Любознательный слушатель может спросить: "Откуда я знаю, что приведенная стоимость проекта Клякса действительно проявляется в рыночной стоимости компании Конус?"

Слайд 11 Чистая приведенная стоимость
На этот вопрос можно ответить так:

Чистая приведенная стоимостьНа этот вопрос можно ответить так:

"Предположим, вы создали новую независимую фирму Клякса, активы которой

образует только проект Клякса. Какова может быть рыночная стоимость фирмы Клякса?

Слайд 12 Чистая приведенная стоимость
Инвесторы могут предположить, какие дивиденды способна

Чистая приведенная стоимостьИнвесторы могут предположить, какие дивиденды способна выплачивать фирма Клякса,

выплачивать фирма Клякса, и дисконтировать эти дивиденды по ожидаемой

норме доходности ценных бумаг со степенью риска, подобной риску фирмы Клякса. Мы с вами уже знаем, что цена акции равна приведенной стоимости прогнозируемых дивидендов.

Слайд 13 Чистая приведенная стоимость
Так как проект Клякса составляет все

Чистая приведенная стоимостьТак как проект Клякса составляет все активы фирмы Клякса,

активы фирмы Клякса, мы можем предположить, что размер дивидендов,

которые будет выплачивать фирма Клякса, точно равен потокам денежных средств, которые мы прогнозируем для проекта Клякса.

Слайд 14 Чистая приведенная стоимость
Кроме того, ставка, по которой инвесторы

Чистая приведенная стоимостьКроме того, ставка, по которой инвесторы могут дисконтировать дивиденды

могут дисконтировать дивиденды фирмы Клякса, равна ставке, по которой

нам следует дисконтировать потоки денежных средств, генерируемые проектом Клякса.

Слайд 15 Чистая приведенная стоимость
Конечно, пример фирмы Клякса - чисто

Чистая приведенная стоимостьКонечно, пример фирмы Клякса - чисто гипотетический. Но если

гипотетический. Но если проект Клякса принимается, инвесторы, владеющие акциями

компании Конус, действительно будут иметь портфель, состоящий из проекта Клякса и других активов компании Конус.

Слайд 16 Чистая приведенная стоимость
Мы знаем, что другие активы компании

Чистая приведенная стоимостьМы знаем, что другие активы компании Конус, рассматриваемые отдельно,

Конус, рассматриваемые отдельно, стоят 90 млн руб. Поскольку мы

можем суммировать стоимости активов, мы в состоянии легко определить стоимость портфеля, рассматривая стоимость проекта Клякса как стоимость отдельного предприятия.

Слайд 17 Чистая приведенная стоимость
Можно уверенно сказать, что определяя приведенную

Чистая приведенная стоимостьМожно уверенно сказать, что определяя приведенную стоимость проекта Клякса,

стоимость проекта Клякса, мы воспроизводим процесс оценки обыкновенных акций

фирмы Клякса на рынках капиталов. Это настолько очевидно, что наш слушатель готов принять этот вывод.

Слайд 18 Чистая приведенная стоимость
У нашего слушателя появляется новый вопрос:

Чистая приведенная стоимостьУ нашего слушателя появляется новый вопрос: «Можно ли уточнить,

«Можно ли уточнить, откуда мы берем ставку дисконтирования при

определении показателя чистой приведенной стоимости проекта?»

Слайд 19 Чистая приведенная стоимость
Эту тему мы уже обсуждали, но

Чистая приведенная стоимостьЭту тему мы уже обсуждали, но вновь рассмотрим суть

вновь рассмотрим суть этой проблемы. Несомненно, точно определить ставку

дисконта трудно. Но довольно легко увидеть, что именно мы пытаемся измерить с помощью этого показателя.

Слайд 20 Чистая приведенная стоимость
Ставка дисконта представляет собой альтернативные издержки

Чистая приведенная стоимостьСтавка дисконта представляет собой альтернативные издержки инвестирования в проект,

инвестирования в проект, а не на рынке капиталов. Иначе

говоря, вместо осуществления проекта Клякса компания Конус всегда может отдать деньги акционерам, и те инвестируют их в финансовые активы.

Слайд 21 Чистая приведенная стоимость
На следующем рисунке представлены альтернативы использования

Чистая приведенная стоимостьНа следующем рисунке представлены альтернативы использования денежных средств:

денежных средств:

Слайд 22 Чистая приведенная стоимость
На этом рисунке показан выбор между

Чистая приведенная стоимостьНа этом рисунке показан выбор между двумя возможными вариантами.

двумя возможными вариантами. Альтернативные издержки осуществления проекта представляют собой

доход, который могли бы получить акционеры, если бы инвестировали свои средства по собственному усмотрению.

Слайд 23 Чистая приведенная стоимость
Когда мы дисконтируем потоки денежных средств

Чистая приведенная стоимостьКогда мы дисконтируем потоки денежных средств по ожидаемой норме

по ожидаемой норме доходности сопоставимых финансовых активов, мы определяем,

сколько инвесторы были бы готовы заплатить за проект Клякса.

Слайд 24 Чистая приведенная стоимость
Еще раз обратим внимание слушателя, что

Чистая приведенная стоимостьЕще раз обратим внимание слушателя, что идея альтернативных издержек

идея альтернативных издержек имеет смысл лишь в том случае,

когда сравниваются активы, которым присуща одинаковая степень риска.

Слайд 25 Чистая приведенная стоимость
В общем случае мы должны выявить

Чистая приведенная стоимостьВ общем случае мы должны выявить активы, риск которых

активы, риск которых эквивалентен риску рассматриваемого проекта, определить ожидаемую

норму доходности этих активов и использовать эту норму в качестве альтернативных издержек, т.е в качестве ставки дисконтирования.

Слайд 26 Чистая приведенная стоимость
Представляется, что теперь любознательный слушатель убедился

Чистая приведенная стоимостьПредставляется, что теперь любознательный слушатель убедился в корректности правила

в корректности правила чистой приведенной стоимости. Но, возможно, он

также слышал и о некоторых других альтернативных критериях оценки инвестиций и хочет узнать, почему в курсе лекций не рассмотрены какие-либо из них.

Слайд 27 Чистая приведенная стоимость
Сейчас мы предлагаем четыре наиболее известных

Чистая приведенная стоимостьСейчас мы предлагаем четыре наиболее известных критерия, альтернативных правилу

критерия, альтернативных правилу чистой приведенной стоимости:
Внутренняя норма доходности.
Срок окупаемости

инвестиций.
Средняя прибыль в расчете на балансовую стоимость активов.
Коэффициент рентабельности.

Слайд 28 Чистая приведенная стоимость
Принимая во внимание эти альтернативные критерии,

Чистая приведенная стоимостьПринимая во внимание эти альтернативные критерии, слушателям стоит напомнить

слушателям стоит напомнить следующие основные особенности правила чистой приведенной

стоимости:

Слайд 29 Чистая приведенная стоимость
Первое правило чистой приведенной стоимости предполагает,

Чистая приведенная стоимостьПервое правило чистой приведенной стоимости предполагает, что стоимость рубля

что стоимость рубля сегодня больше его стоимости завтра, поскольку

сегодня рубль может быть инвестирован и сразу начнет приносить процентный доход. Любое правило инвестирования, которое не учитывает стоимости денег во времени, не может быть корректным.

Слайд 30 Чистая приведенная стоимость

Второе правило - чистая приведенная стоимость

Чистая приведенная стоимостьВторое правило - чистая приведенная стоимость зависит исключительно от

зависит исключительно от прогнозируемых потоков денежных средств, генерируемых проектом,

и от альтернативных издержек.

Слайд 31 Чистая приведенная стоимость
Любое правило инвестирования, на которое влияют

Чистая приведенная стоимостьЛюбое правило инвестирования, на которое влияют предпочтения менеджеров, выбранные

предпочтения менеджеров, выбранные компанией принципы учетной политики, рентабельность уже

осуществляемой компанией деятельности или рентабельность других независимых проектов, приведет к принятию худших решений.

Слайд 32 Чистая приведенная стоимость
Третье правило — поскольку приведенные стоимости

Чистая приведенная стоимостьТретье правило — поскольку приведенные стоимости измеряются в текущих

измеряются в текущих рублях, мы можем их суммировать. То

есть показатель чистой приведенной стоимости обладает свойством аддитивности. Поэтому, если реализуются два проекта А и B, чистая приведенная стоимость этих двух проектов равна:
NPV(A) + NPV(B) = NPV (A+B).

Слайд 33 Чистая приведенная стоимость
Это свойство аддитивности стоимостей имеет важное

Чистая приведенная стоимостьЭто свойство аддитивности стоимостей имеет важное практическое значение. Предположим,

практическое значение. Предположим, проект В имеет отрицательную чистую приведенную

стоимость. Если объединить его с проектом А, то проект (А + В) будет иметь меньшую чистую приведенную стоимость, чем только проект А.

Слайд 34 Чистая приведенная стоимость
Поэтому маловероятно, что аналитик ошибется в

Чистая приведенная стоимостьПоэтому маловероятно, что аналитик ошибется в оценке плохого проекта

оценке плохого проекта В просто потому, что он соединен

с хорошим проектом А. Как мы увидим дальше, альтернативные критерии не обладают этим свойством аддитивности.

Слайд 35 Чистая приведенная стоимость
И если аналитик будет невнимателен, то

Чистая приведенная стоимостьИ если аналитик будет невнимателен, то может впасть в

может впасть в заблуждение, решив, что пакет, состоящий из

хорошего и плохого проектов, лучше, чем только хороший проект.

Слайд 36 Срок окупаемости
Компании часто требуют, чтобы первоначальные инвестиции в

Срок окупаемостиКомпании часто требуют, чтобы первоначальные инвестиции в какой-либо проект окупались

какой-либо проект окупались в течение некоторого определенного обозримого периода

времени.
Период окупаемости проекта определяется рядом лет, в течение которых совокупные прогнозируемые потоки денежных средств покрывают первоначальные инвестиции. Рассмотрим проекты А и В:

Слайд 37 Срок окупаемости

Срок окупаемости

Слайд 38 Срок окупаемости
Первоначальные инвестиции в проект А составляют 200

Срок окупаемостиПервоначальные инвестиции в проект А составляют 200 тыс. руб. (I0=

тыс. руб. (I0= -200 000) и обеспечивают единственный приток

денежных средств в году 1 в сумме 200 тыс. руб. Предположим, альтернативные издержки равны 10%. Тогда чистая приведенная стоимость проекта А составляет -18 180 руб.:

Слайд 39 Срок окупаемости
Проект В также требует первоначальных инвестиций в

Срок окупаемостиПроект В также требует первоначальных инвестиций в размере 200 тыс.

размере 200 тыс. руб., но он обеспечивает несколько притоков

денежных средств: по 100 тыс. руб. в годы 1 и 2 и 400 тыс. руб. в году 3. При альтернативных издержках, равных 10%, чистая приведенная стоимость проекта В составит +274 100 руб.:

Слайд 40 Срок окупаемости
Теперь давайте посмотрим, как быстро окупятся первоначальные

Срок окупаемостиТеперь давайте посмотрим, как быстро окупятся первоначальные инвестиции по каждому

инвестиции по каждому из проектов. Что касается проекта А,

то первоначальные инвестиции в сумме 200 тыс. руб. окупятся за первый год, в то время как по проекту В такие же по сумме инвестиции окупятся за два года.

Слайд 41 Срок окупаемости
Если компания придерживается правила, что период окупаемости

Срок окупаемостиЕсли компания придерживается правила, что период окупаемости должен быть не

должен быть не больше одного года, то она может

принять только проект А, если же ее устраивает срок окупаемости в два года или более, то она может принять как проект А, так и проект В.

Слайд 42 Срок окупаемости

Следовательно, вне зависимости от выбора

Срок окупаемости Следовательно, вне зависимости от выбора периода окупаемости правило окупаемости

периода окупаемости правило окупаемости дает результаты, отличные от результатов,

получаемых при использовании правила чистой приведенной стоимости.

Слайд 43 Срок окупаемости
Причина расхождения в результатах состоит в

Срок окупаемости Причина расхождения в результатах состоит в том, что в

том, что в соответствии с правилом окупаемости равноценными считаются

все потоки денежных средств, возникающие до истечения срока окупаемости, и совсем не учитываются последующие потоки денежных средств.

Слайд 44 Срок окупаемости
Например, все три следующих проекта имеют одинаковый

Срок окупаемостиНапример, все три следующих проекта имеют одинаковый период окупаемости, равный двум годам:

период окупаемости, равный двум годам:


Слайд 45 Срок окупаемости
Согласно правилу окупаемости, все эти три проекта

Срок окупаемостиСогласно правилу окупаемости, все эти три проекта одинаково привлекательны. Но

одинаково привлекательны. Но проект А имеет более высокую чистую

приведенную стоимость, чем проект В, при любой положительной процентной ставке (по 100 тыс. руб. и в первом и во втором году стоят больше, чем 200 тыс. руб. во втором году). А проект С имеет более высокую чистую приведенную стоимость, чем проекты А и В.

Слайд 46 Срок окупаемости
Руководствуясь правилом окупаемости, компания должна определить соответствующий

Срок окупаемостиРуководствуясь правилом окупаемости, компания должна определить соответствующий период окупаемости. Если

период окупаемости. Если компания придерживается одного и того же

периода окупаемости независимо от продолжительности экономической жизни проекта, то это приводит к принятию большого количества краткосрочных проектов и совсем незначительного числа долгосрочных.

Слайд 47 Срок окупаемости
Если в среднем периоды окупаемости достаточно продолжительные,

Срок окупаемостиЕсли в среднем периоды окупаемости достаточно продолжительные, некоторые проекты, принятые

некоторые проекты, принятые корпорацией, будут иметь отрицательную чистую приведенную

стоимость; если же в среднем периоды окупаемости короткие, она откажется от некоторых проектов с положительными чистыми приведенными стоимостями.

Слайд 48 Срок окупаемости

Многие фирмы, которые действуют в соответствии с

Срок окупаемостиМногие фирмы, которые действуют в соответствии с принципом окупаемости, выбирают

принципом окупаемости, выбирают продолжительность периода окупаемости, как правило, предположительно.


Слайд 49 Срок окупаемости
Есть возможность поступать более обоснованно. Если вам

Срок окупаемостиЕсть возможность поступать более обоснованно. Если вам известна типичная схема

известна типичная схема потоков денежных средств, тогда вы можете

определить период окупаемости, для которого чистая приведенная стоимость будет максимальна .

Слайд 50 Срок окупаемости
Если в среднем инвестиции осуществляются равномерно в

Срок окупаемостиЕсли в среднем инвестиции осуществляются равномерно в течение жизни проекта,

течение жизни проекта, оптимальный период окупаемости по правилу окупаемости

равен:
tPBP = 1/r – 1/[r×(1+r)n],
где п - продолжительность жизни проекта.

Слайд 51 Срок окупаемости
Однако этот принцип "оптимального" периода окупаемости работает

Срок окупаемостиОднако этот принцип

только для проектов с типовой схемой потоков денежных средств.

Поэтому все же лучше руководствоваться правилом чистой приведенной стоимости.

Слайд 52 Срок окупаемости
Некоторые финансовые менеджеры, прежде чем определять период

Срок окупаемостиНекоторые финансовые менеджеры, прежде чем определять период окупаемости, дисконтируют потоки

окупаемости, дисконтируют потоки денежных средств.
Правило дисконтированной

окупаемости базируется на вопросе:
в течение какого времени должен осуществляться проект, чтобы он имел смысл с точки зрения чистой приведенной стоимости?

Слайд 53 Срок окупаемости
Эта модификация принципа окупаемости позволяет избежать ошибок,

Срок окупаемостиЭта модификация принципа окупаемости позволяет избежать ошибок, связанных с единообразной

связанных с единообразной оценкой всех потоков денежных средств, возникающих

за время окупаемости. Однако принцип дисконтированной окупаемости все же не учитывает потоки денежных средств, возникающие за пределами периода окупаемости.


Слайд 54 Срок окупаемости
Предположим, есть два взаимоисключающих инвестиционных проекта, А

Срок окупаемостиПредположим, есть два взаимоисключающих инвестиционных проекта, А и В. Каждый

и В. Каждый проект требует 2,0 млн руб. первоначальных

инвестиций, и ожидается, что каждый из них начинает давать потоки денежных средств с первого года.

Слайд 55 Срок окупаемости
Потоки денежных средств для проекта А равны

Срок окупаемостиПотоки денежных средств для проекта А равны 600 тыс. руб.

600 тыс. руб. и проект продолжается 6 лет.
Потоки

денежных средств проекта В равны 525 тыс. руб., но его продолжительность 10 лет. Соответствующая ставка дисконта для каждого проекта равна 10%. Определим для обоих проектов показатель чистой приведенной стоимости:

Слайд 56 Срок окупаемости






Проект В очевидно привлекательнее проекта А, исходя

Срок окупаемостиПроект В очевидно привлекательнее проекта А, исходя из чистой приведенной стоимости.

из чистой приведенной стоимости.

Слайд 57 Срок окупаемости

Ежегодное поступление денег по проекту А больше,

Срок окупаемостиЕжегодное поступление денег по проекту А больше, чем по проекту

чем по проекту В, и поэтому, очевидно, проект А

имеет более короткий период дисконтированной окупаемости.

Слайд 58 Срок окупаемости
Период окупаемости проекта А немногим меньше 5

Срок окупаемостиПериод окупаемости проекта А немногим меньше 5 лет, так как

лет, так как приведенная стоимость 600 тыс. руб. при

ставке 10% за 5 лет составит 2 274 472 руб. Период окупаемости проекта В немногим больше 5 лет, поскольку приведенная стоимость 525 тыс. руб. за 5 лет составит 1 990 163 руб., т.е. меньше 2,0 млн. руб.

Слайд 59 Срок окупаемости
Дисконтированная окупаемость служит лучшим критерием, чем не

Срок окупаемостиДисконтированная окупаемость служит лучшим критерием, чем не дисконтированная. Она учитывает,

дисконтированная. Она учитывает, что рубль в начале периода окупаемости

стоит больше, чем рубль в конце периода окупаемости.

Слайд 60 Срок окупаемости
Этот показатель полезный, но не слишком. Принцип

Срок окупаемостиЭтот показатель полезный, но не слишком. Принцип дисконтированной окупаемости все

дисконтированной окупаемости все же зависит от произвольного выбора периода

окупаемости и не учитывает потоки денежных средств за его пределами.

Слайд 61 Бухгалтерская норма рентабельности
Некоторые компании оценивают инвестиционные проекты по

Бухгалтерская норма рентабельностиНекоторые компании оценивают инвестиционные проекты по бухгалтерской норме рентабельности.

бухгалтерской норме рентабельности. Для вычисления бухгалтерской нормы рентабельности используется

формула:
RA = Pav/Iav,
где Pav - средняя прогнозируемую прибыль от проекта за вычетом амортизации и налогов;
Iav - средняя балансовая стоимость инвестиций.

Слайд 62 Бухгалтерская норма рентабельности
Затем этот коэффициент сравнивается с бухгалтерской

Бухгалтерская норма рентабельностиЗатем этот коэффициент сравнивается с бухгалтерской нормой рентабельности фирмы

нормой рентабельности фирмы в целом или с какими-либо внешними

критериями, например, со средней бухгалтерской нормой рентабельности отрасли.

Слайд 63 Бухгалтерская норма рентабельности
Пример. В следующей таблице представлен

Бухгалтерская норма рентабельностиПример. В следующей таблице представлен прогнозный отчет о прибыли

прогнозный отчет о прибыли для проекта А за три

года.

Слайд 64 Бухгалтерская норма рентабельности
Средняя чистая прибыль составит:
Pav=(50000+40000+30000)/3=40

Бухгалтерская норма рентабельностиСредняя чистая прибыль составит: Pav=(50000+40000+30000)/3=40 000 руб. Для упрощения

000 руб. Для упрощения мы не берем в расчет

налог на прибыль.
Необходимые инвестиции в год t = 0 равны 180 000 руб. Затем эта сумма уменьшается с постоянным темпом на 60 000 руб. в год (износ основных средств) .

Слайд 65 Бухгалтерская норма рентабельности
Таким образом, номинальная стоимость новых инвестиций

Бухгалтерская норма рентабельностиТаким образом, номинальная стоимость новых инвестиций снижается со 180

снижается со 180 000 руб. в 2010 году до

нуля в 2013 году:

Слайд 66 Бухгалтерская норма рентабельности
Средняя остаточная балансовая стоимость инвестиций равна:

Бухгалтерская норма рентабельностиСредняя остаточная балансовая стоимость инвестиций равна: Iav

Iav = (120 000 +

60 000+0)/3 = 60 000 руб.
Подставив полученные данные, находим значение бухгалтерской нормы рентабельности инвестиций:
RA = Pav/Iav=40 000/60 000=0,667 или 66,7 %
Таким образом, проект А можно принять, если плановая бухгалтерская норма рентабельности компании будет ниже 66,7 %.

Слайд 67 Бухгалтерская норма рентабельности
Данный показатель эффективности инвестиционного проекта имеет

Бухгалтерская норма рентабельностиДанный показатель эффективности инвестиционного проекта имеет несколько серьезных недостатков.

несколько серьезных недостатков.
Первый: поскольку он отражает только среднюю

прибыль в расчете на балансовую стоимость инвестиций, то не учитывается тот факт, что немедленные поступления имеют большую стоимость, чем отдаленные во времени.

Слайд 68 Бухгалтерская норма рентабельности
Если в правиле окупаемости инвестиций не

Бухгалтерская норма рентабельностиЕсли в правиле окупаемости инвестиций не принимаются во внимание

принимаются во внимание более удаленные во времени потоки денежных

средств, то в правиле рентабельности в расчете на балансовую стоимость активов им придается слишком большое значение.

Слайд 69 Бухгалтерская норма рентабельности
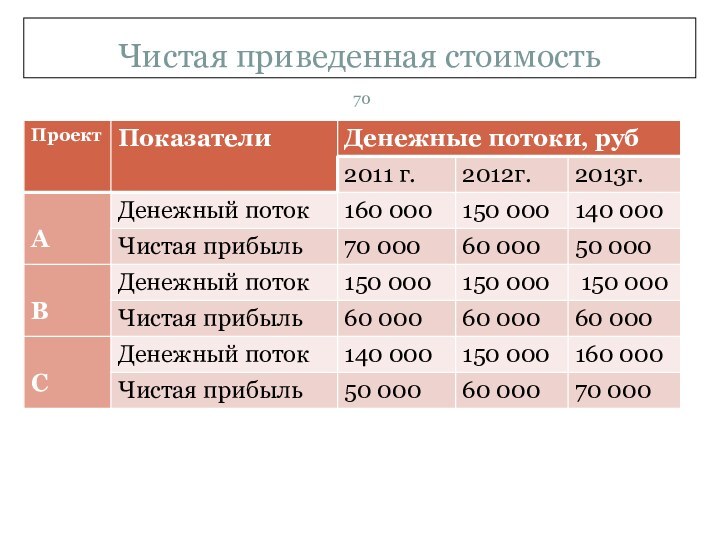
В следующей таблице приводятся данные по

Бухгалтерская норма рентабельностиВ следующей таблице приводятся данные по трем проектам. Проекты

трем проектам. Проекты В и С, имеют такие же

показатели, как и проект А (балансовая стоимость инвестиций, средняя бухгалтерская прибыль и средняя бухгалтерская рентабельность). Однако при этом чистая приведенная стоимость проекта А выше, чем проектов Б и В, поскольку по проекту А большая доля потоков денежных средств приходится на первые годы.

Слайд 70 Чистая приведенная стоимость

Чистая приведенная стоимость

Слайд 71 Бухгалтерская норма рентабельности
Во-вторых, показатель средней прибыли в расчете

Бухгалтерская норма рентабельностиВо-вторых, показатель средней прибыли в расчете на балансовую стоимость

на балансовую стоимость инвестиций опирается на бухгалтерскую прибыль, а

не на создаваемые проектом потоки денежных средств. Потоки денежных средств и бухгалтерская прибыль часто сильно различаются.

Слайд 72 Бухгалтерская норма рентабельности
Например, бухгалтеры относят некоторые направления оттоков

Бухгалтерская норма рентабельностиНапример, бухгалтеры относят некоторые направления оттоков денежных средств к

денежных средств к капитальным затратам, а другие - к

операционным расходам. Конечно, операционные расходы сразу вычитаются из валовой выручки любого года.

Слайд 73 Бухгалтерская норма рентабельности

Возмещение капитальных затрат происходит согласно произвольно

Бухгалтерская норма рентабельностиВозмещение капитальных затрат происходит согласно произвольно выбранной бухгалтером схеме.

выбранной бухгалтером схеме. Затем из дохода каждого года вычитаются

амортизационные отчисления.

Слайд 74 Бухгалтерская норма рентабельности

Поэтому средняя прибыль в расчете на

Бухгалтерская норма рентабельностиПоэтому средняя прибыль в расчете на балансовую стоимость активов

балансовую стоимость активов зависит от того, какие статьи расходов

бухгалтер относит к капитальным затратам и как быстро они амортизируются.

Слайд 75 Бухгалтерская норма рентабельности

Однако решения бухгалтера не в состоянии

Бухгалтерская норма рентабельностиОднако решения бухгалтера не в состоянии воздействовать на величину

воздействовать на величину потоков денежных средств и поэтому не

должны влиять на решения о принятии проекта или отказе от него.

Слайд 76 Бухгалтерская норма рентабельности
Компания, использующая показатель средней прибыли в

Бухгалтерская норма рентабельностиКомпания, использующая показатель средней прибыли в расчете на балансовую

расчете на балансовую стоимость активов, должна выбрать критерий для

оценки проекта. Это решение также произвольно. Иногда в качестве критерия фирма использует текущую бухгалтерскую прибыль.

Слайд 77 Бухгалтерская норма рентабельности
В таких случаях компании с высокими

Бухгалтерская норма рентабельностиВ таких случаях компании с высокими нормами рентабельности своего

нормами рентабельности своего уже осуществляемого бизнеса порой отказываются от

хороших проектов, а компании с низкими нормами рентабельности соглашаются на плохие.

Слайд 78 Бухгалтерская норма рентабельности
Правило окупаемости плохой критерий. Правило средней

Бухгалтерская норма рентабельностиПравило окупаемости плохой критерий. Правило средней прибыли в расчете

прибыли в расчете на балансовую стоимость активов, возможно, еще

хуже, поскольку оно не учитывает альтернативную стоимость денег и не опирается на потоки денежных средств проекта.

Слайд 79 Внутренняя норма доходности
Следующим критерием оценки эффективности инвестиционного проекта

Внутренняя норма доходностиСледующим критерием оценки эффективности инвестиционного проекта является показатель внутренней

является показатель внутренней нормы доходности (IRR). Этот критерий имеет

гораздо более почтенную репутацию и рекомендуется во многих работах, посвященных финансам.

Слайд 80 Внутренняя норма доходности
И когда мы будем анализировать достоинства

Внутренняя норма доходностиИ когда мы будем анализировать достоинства и недостатки этого

и недостатки этого показателя, то, конечно, мы более подробно

остановимся на его недостатках, то не оттого, что они многочисленны, а потому, что они менее очевидны.

Слайд 81 Внутренняя норма доходности
Прежде всего, обратим внимание нашего слушателя

Внутренняя норма доходностиПрежде всего, обратим внимание нашего слушателя на возможность выражения

на возможность выражения чистой приведенной стоимости инвестиционного проекта через

норму доходности. В этом случае необходимо следовать следующему правилу:
реализуй те инвестиционные возможности, для которых норма доходности инвестированного капитала выше альтернативных издержек.

Слайд 82 Внутренняя норма доходности
Данное утверждение, если его правильно

Внутренняя норма доходности Данное утверждение, если его правильно интерпретировать, безусловно, корректно.

интерпретировать, безусловно, корректно. Однако правильная интерпретация не всегда легко

даётся применительно к долгосрочным инвестиционным проектам.


Слайд 83 Внутренняя норма доходности
При определении нормы доходности (rN) инвестиций,

Внутренняя норма доходностиПри определении нормы доходности (rN) инвестиций, которые приносят единственный

которые приносят единственный поток денежных средств через один год,

двусмысленности не возникает:
rN = CF/I – 1, (1)
где CF – денежный поток, генерируемый инвестированным капиталом, руб.
I – инвестированный капитал, руб.

Слайд 84 Внутренняя норма доходности
Или же мы можем записать формулу

Внутренняя норма доходностиИли же мы можем записать формулу чистой приведенной стоимости

чистой приведенной стоимости инвестиций и определить ставку дисконта, при

которой показатель NPV
равен нулю, т.е.:
NPV = -I + CF1/(1+r) =0, (2)

Слайд 85 Внутренняя норма доходности
где I – инвестированный капитал в

Внутренняя норма доходностигде I – инвестированный капитал в период 0, руб.

период 0, руб.
CF1–денежный поток, полученный через

год, руб.;
r – ставка дисконтирования, доли ед.
На основе формулы (2) мы можем записать:
r = CF1/ I – 1. (3)

Слайд 86 Внутренняя норма доходности
Конечно, CF1 — это поступления, I—

Внутренняя норма доходностиКонечно, CF1 — это поступления, I— требуемые инвестиции, и,

требуемые инвестиции, и, таким образом, оба наших уравнения (1)

и (3) говорят об одном и том же. Таким образом, ставка дисконтирования, при которой чистая приведенная стоимость равняется нулю, является также нормой доходности инвестированного капитала.

Слайд 87 Внутренняя норма доходности
К сожалению, нет вполне удовлетворительного способа

Внутренняя норма доходностиК сожалению, нет вполне удовлетворительного способа найти точную норму

найти точную норму доходности долгосрочных активов. Наиболее приемлема для

этих целей так называемая норма доходности дисконтированных потоков денежных средств, или внутренняя норма доходности (IRR) инвестированного капитала.

Слайд 88 Внутренняя норма доходности
Показатель внутренней нормы доходности часто используется

Внутренняя норма доходностиПоказатель внутренней нормы доходности часто используется при оценке инвестиционных

при оценке инвестиционных проектов и в сфере финансов. Это

удобный критерий, но, как мы еще увидим, он может быть и ошибочным. Поэтому нам следует знать, как ее вычислять и как верно применять.

Слайд 89 Внутренняя норма доходности
Напомним слушателям еще раз, что внутренняя

Внутренняя норма доходностиНапомним слушателям еще раз, что внутренняя норма доходности (IRR)

норма доходности (IRR) определяется как ставка дисконта, при которой

чистая приведенная стоимость равна нулю.

Слайд 90 Внутренняя норма доходности
Это означает, что для определения IRR

Внутренняя норма доходностиЭто означает, что для определения IRR инвестиционного проекта продолжительностью

инвестиционного проекта продолжительностью t лет мы должны определить ставку

дисконта r из следующего общего выражения:


Слайд 91 Внутренняя норма доходности
Искомая ставка дисконтирования и будет внутренней

Внутренняя норма доходностиИскомая ставка дисконтирования и будет внутренней нормой доходности инвестиционного

нормой доходности инвестиционного проекта. На практике внутреннюю норму доходности

обычно находят методом подбора. Метод подбора ставки дисконтирования, при которой выполняется условие NPV = 0, покажем на следующем примере.

Слайд 92 Внутренняя норма доходности
Пример. Инвестору предлагается купить финансовый инструмент,

Внутренняя норма доходностиПример. Инвестору предлагается купить финансовый инструмент, стоимость которого равна

стоимость которого равна 7704 долл. Этот инструмент имеет срок

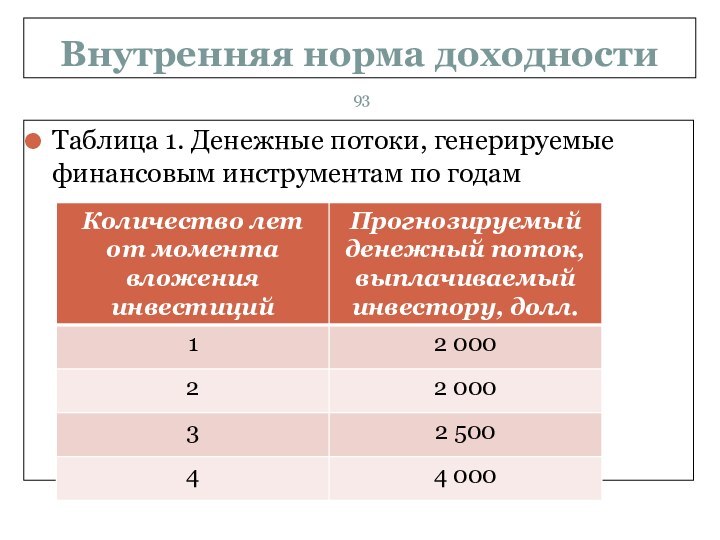
жизни, равный 4 годам. Эмитент каждый год предполагает выплачивать держателю инструмента денежные потоки, представленные в следующей таблице 1:

Слайд 93 Внутренняя норма доходности
Таблица 1. Денежные потоки, генерируемые финансовым

Внутренняя норма доходностиТаблица 1. Денежные потоки, генерируемые финансовым инструментам по годам

инструментам по годам

Слайд 94 Внутренняя норма доходности
Чтобы определить доходность инвестированного капитала, мы

Внутренняя норма доходностиЧтобы определить доходность инвестированного капитала, мы должны перебрать разные

должны перебрать разные ставки дисконтирования, и найти ту, которая

делает сумму текущих стоимостей будущих денежных потоков равной 7704 долл., т.е. цене инструмента. Ставка дисконтирования, равная 10%, делает сумму текущих стоимостей будущих денежных потоков следующей (табл.2):

Слайд 95 Внутренняя норма доходности
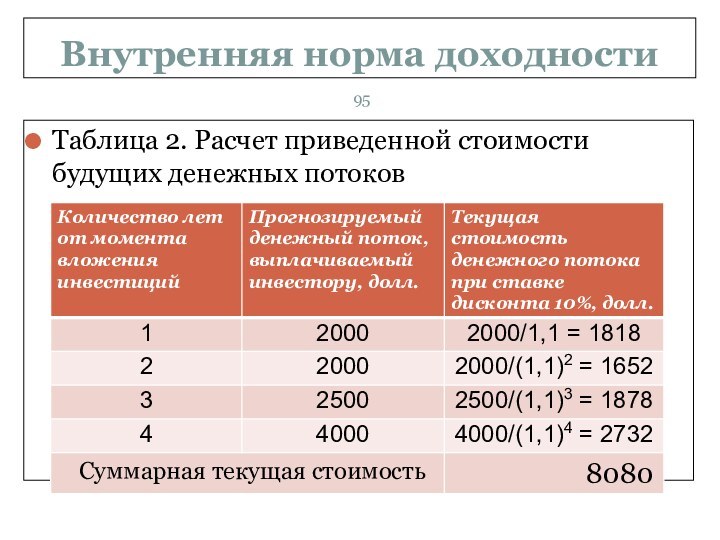
Таблица 2. Расчет приведенной стоимости будущих

Внутренняя норма доходностиТаблица 2. Расчет приведенной стоимости будущих денежных потоков

денежных потоков

Слайд 96 Внутренняя норма доходности
Полученный результат показывает, что при ставке

Внутренняя норма доходностиПолученный результат показывает, что при ставке дисконтирования 10 %

дисконтирования 10 % не выполняется условие NPV = 0,

поскольку сумма приведенных будущих денежных потоков больше инвестированного капитала (8080>7704), и поэтому эта ставка не может служить показателем IRR. Теперь выбираем большую ставку дисконта, например,14%.

Слайд 97 Внутренняя норма доходности
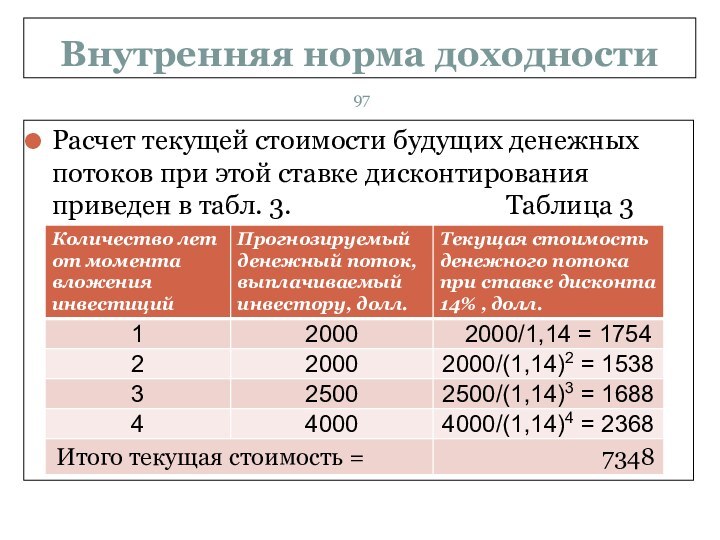
Расчет текущей стоимости будущих денежных потоков

Внутренняя норма доходностиРасчет текущей стоимости будущих денежных потоков при этой ставке

при этой ставке дисконтирования приведен в табл. 3.

Таблица 3


Слайд 98 Внутренняя норма доходности
При дисконтной ставке, равной 14 %,

Внутренняя норма доходностиПри дисконтной ставке, равной 14 %, вновь не выполняется

вновь не выполняется условие NPV=0, поскольку приведенная сумма будущих

денежных потоков меньше суммы инвестированного капитала (7 348<7 704) и поэтому эта ставка не может служить показателем IRR. Следовательно, надо взять меньшее значение дисконтной ставки.

Слайд 99 Внутренняя норма доходности
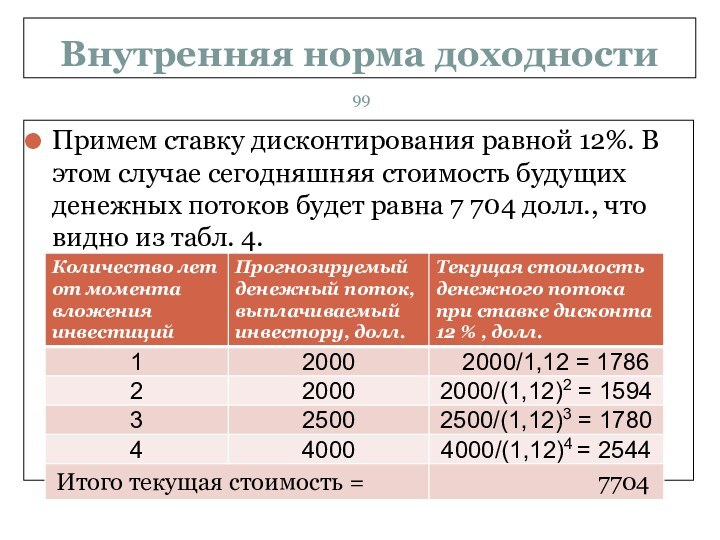
Примем ставку дисконтирования равной 12%. В

Внутренняя норма доходностиПримем ставку дисконтирования равной 12%. В этом случае сегодняшняя

этом случае сегодняшняя стоимость будущих денежных потоков будет равна

7 704 долл., что видно из табл. 4.

Слайд 100 Внутренняя норма доходности
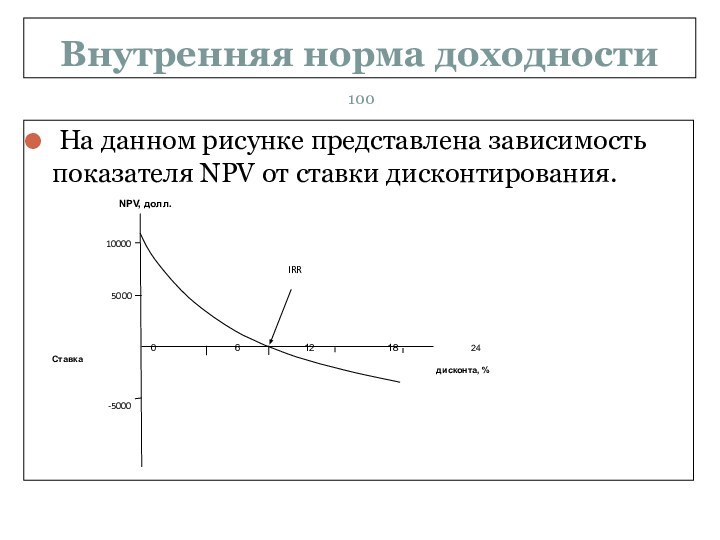
На данном рисунке представлена зависимость

Внутренняя норма доходности На данном рисунке представлена зависимость показателя NPV от

показателя NPV от ставки дисконтирования.

NPV, долл.


10000

IRR

5000



0 6 12 18 24 Ставка
дисконта, %


-5000


Слайд 101 Внутренняя норма доходности
Из этого рисунка видно, что ставка

Внутренняя норма доходностиИз этого рисунка видно, что ставка дисконта на уровне

дисконта на уровне 12 % дает искомую чистую приведенную

стоимость, равную нулю. Следовательно, внутренняя норма доходности проекта равна 12 %.

Слайд 102 Внутренняя норма доходности
Согласно правилу внутренней нормы доходности инвестиционный

Внутренняя норма доходностиСогласно правилу внутренней нормы доходности инвестиционный проект следует принять,

проект следует принять, если альтернативные издержки меньше, чем внутренняя

норма доходности. Доказательством этого служит график на рисунке, представленном выше.

Слайд 103 Внутренняя норма доходности
Если альтернативные издержки меньше внутренней нормы

Внутренняя норма доходностиЕсли альтернативные издержки меньше внутренней нормы доходности, равной 12

доходности, равной 12 %, тогда при дисконтировании по ставке,

равной альтернативным издержкам, проект будет иметь положительную чистую приведенную стоимость.

Слайд 104 Внутренняя норма доходности
Если альтернативные издержки равны внутренней норме

Внутренняя норма доходностиЕсли альтернативные издержки равны внутренней норме доходности, проект имеет

доходности, проект имеет нулевую чистую приведенную стоимость. И если

альтернативные издержки превышают внутреннюю норму доходности, проект имеет отрицательную чистую приведенную стоимость.

Слайд 105 Внутренняя норма доходности
Следовательно, когда мы сравниваем альтернативные издержки

Внутренняя норма доходностиСледовательно, когда мы сравниваем альтернативные издержки инвестирования с внутренней

инвестирования с внутренней нормой доходности нашего проекта, мы действительно

можем сказать, имеет ли проект положительную чистую приведенную стоимость.

Слайд 106 Внутренняя норма доходности
Это верно применительно не только к

Внутренняя норма доходностиЭто верно применительно не только к нашему примеру. Вывод,

нашему примеру. Вывод, сделанный согласно данному правилу, будет тем

же, что и согласно правилу чистой приведенной стоимости всякий раз, когда чистая приведенная стоимость проекта является постепенно убывающей функцией ставки дисконта.

Слайд 107 Внутренняя норма доходности
Обратим внимание слушателя на очень важное

Внутренняя норма доходностиОбратим внимание слушателя на очень важное замечание по показателю

замечание по показателю IRR. Некоторые люди путают понятия внутренней

нормы доходности и альтернативных издержек, поскольку оба выступают в качестве ставки дисконта в формуле чистой приведенной стоимости.

Слайд 108 Внутренняя норма доходности
Внутренняя норма доходности является измерителем рентабельности,

Внутренняя норма доходностиВнутренняя норма доходности является измерителем рентабельности, которая зависит исключительно

которая зависит исключительно от величины и времени возникновения потоков

денежных средств проекта. Альтернативные издержки представляют собой критерий рентабельности, который мы используем для определения того, сколько стоит проект.

Слайд 109 Внутренняя норма доходности
Величина альтернативных издержек устанавливается на рынках

Внутренняя норма доходностиВеличина альтернативных издержек устанавливается на рынках капиталов. Они представляют

капиталов. Они представляют собой ожидаемую норму доходности других активов,

риск которых сопоставим с риском оцениваемого нами проекта.

Слайд 110 Внутренняя норма доходности
Многие финансовые менеджеры предпочитают в качестве

Внутренняя норма доходностиМногие финансовые менеджеры предпочитают в качестве критерия использовать не

критерия использовать не чистую приведенную стоимость, а внутреннюю норму

доходности. Хотя, эти два критерия формально эквивалентны, правило внутренней нормы доходности таит в себе несколько ловушек.

Слайд 111 Внутренняя норма доходности
Заблуждение 1. Не у всех денежных

Внутренняя норма доходностиЗаблуждение 1. Не у всех денежных потоков чистая приведенная

потоков чистая приведенная стоимость уменьшается с ростом ставки дисконта.

Рассмотрим два следующих проекта А и B:






Слайд 112 Внутренняя норма доходности
Внутренняя норма доходности каждого из проектов

Внутренняя норма доходностиВнутренняя норма доходности каждого из проектов составляет 50%,что видно

составляет 50%,что видно из следующих расчетов:
Проект А: -12

000+ 18 000/1,50 = 0
Проект В: +12 000 – 18 000/1,50 = 0.

Слайд 113 Внутренняя норма доходности
Означает ли это, что оба проекта

Внутренняя норма доходностиОзначает ли это, что оба проекта одинаково привлекательны? Ясно,

одинаково привлекательны? Ясно, что нет, так как в проекте

А, когда мы изначально выплачиваем 12 000 руб., мы даем взаймы по ставке 50%, а в проекте Б, где мы изначально получаем 12 000 руб., мы берем взаймы по ставке 50%.

Слайд 114 Внутренняя норма доходности
Когда мы предоставляем кредит, мы хотим

Внутренняя норма доходностиКогда мы предоставляем кредит, мы хотим получить высокую норму

получить высокую норму доходности; когда же мы берем деньги

взаймы, мы хотим, чтобы норма доходности была низкой.

Слайд 115 Внутренняя норма доходности
Давайте для наших проектов увеличим ставку

Внутренняя норма доходностиДавайте для наших проектов увеличим ставку дисконта до 25

дисконта до 25 % и определим показатель NPV. Мы

знаем, что с увеличением дисконтной ставки показатель NPV будет уменьшаться. Однако для проекта В мы получим увеличение показателя NPV, что видно из следующего расчета:
NPVA = -12 000 + 18 000/1,25 = 2 400 руб.
NPVB = +12 000 – 18 000/1,25 = - 2 400 руб.



Слайд 116 Внутренняя норма доходности
Таким образом, показатель NPV для проекта

Внутренняя норма доходностиТаким образом, показатель NPV для проекта А снизился с

А снизился с 4 000 до 2 400 руб.,

а для проекта В увеличился с -4000 до -2400 руб.
Очевидно, что в этом случае метод внутренней нормы доходности, как мы его представили выше, работать не будет; мы должны найти внутреннюю норму доходности, значение которой меньше альтернативных издержек.

Слайд 117 Внутренняя норма доходности
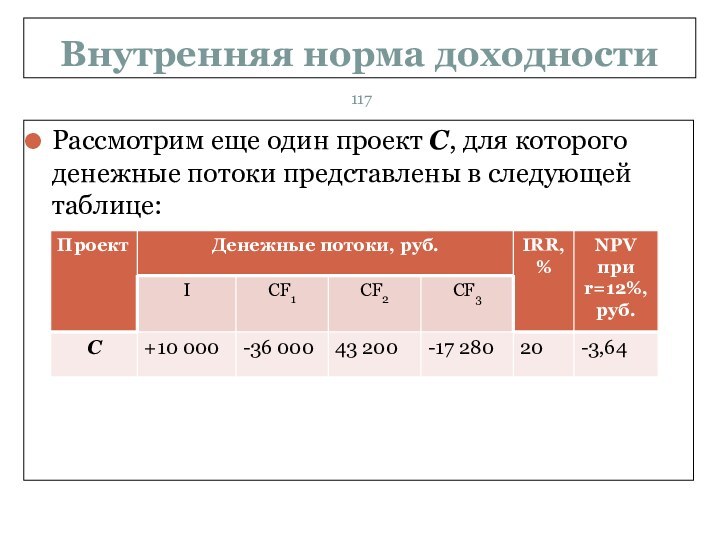
Рассмотрим еще один проект С, для

Внутренняя норма доходностиРассмотрим еще один проект С, для которого денежные потоки представлены в следующей таблице:

которого денежные потоки представлены в следующей таблице:

Слайд 118 Внутренняя норма доходности
Расчеты показывают, чистая приведенная стоимость проекта

Внутренняя норма доходностиРасчеты показывают, чистая приведенная стоимость проекта С равна нулю

С равна нулю при ставке дисконта 20%. Если альтернативные

издержки равны 12%, это значит, что проект стоит осуществлять. В какой-то степени проект С аналогичен получению кредита, поскольку мы получаем деньги сейчас и возвращаем их в первый период.

Слайд 119 Внутренняя норма доходности
В какой-то степени он аналогичен также

Внутренняя норма доходностиВ какой-то степени он аналогичен также предоставлению займа, поскольку

предоставлению займа, поскольку в период 1 мы отдаем деньги

и получаем их обратно в период 2. Следует ли нам принять проект или же лучше отказаться от него? Единственный способ найти ответ, это оценить его чистую приведенную стоимость.

Слайд 120 Внутренняя норма доходности
Показатель NPV проекта С растёт с

Внутренняя норма доходностиПоказатель NPV проекта С растёт с ростом ставки дисконта.

ростом ставки дисконта. Если альтернативные издержки равны 12% (т.

е. меньше внутренней нормы доходности), проект имеет небольшую отрицательную чистую приведенную стоимость (-3,64 руб.), и нам следует отказаться от проекта.

Слайд 121 Внутренняя норма доходности
При ставке дисконтирования 25% показатель NPV

Внутренняя норма доходностиПри ставке дисконтирования 25% показатель NPV для проекта С

для проекта С будет равен 0,64, то есть будет

больше нуля а при r =40 % чистая приведенная стоимость проекта будет равна 29,15 руб.

Слайд 122 Внутренняя норма доходности
Заблуждение 2. Иногда слушатель предполагает, что

Внутренняя норма доходностиЗаблуждение 2. Иногда слушатель предполагает, что показатель IRR для

показатель IRR для проекта может быть только один, как,

например, в наших предыдущих примерах.
Если рассматривается проект, в котором денежные потоки меняют свой знак, то в этом случае этот проект будет иметь столько показателей внутренней нормы доходности, сколько раз в проекте денежный поток менял свой знак.

Слайд 123 Внутренняя норма доходности
Рассмотрим, например, проект Лямбда. Затраты по

Внутренняя норма доходностиРассмотрим, например, проект Лямбда. Затраты по нему составляют 10

нему составляют 10 000 долл., и он приносит вам

в первый год 72 000 долл. Затем во втором году вы должны выплатить 72 000 долл. (Существует множество проектов, по окончании которых происходит отток денежных средств).

Слайд 124 Внутренняя норма доходности
Существуют два значения ставки дисконта, при

Внутренняя норма доходностиСуществуют два значения ставки дисконта, при которых чистая приведенная

которых чистая приведенная стоимость равна нулю:




NPV = -10000+72000/1,2 –

72000/(1,2)2 = 0
NPV = -10000 + 72000/6 – 72000/(6)2 = 0


Слайд 125 Внутренняя норма доходности
Таким образом, внутренняя норма доходности инвестиций

Внутренняя норма доходностиТаким образом, внутренняя норма доходности инвестиций составляет 20% и

составляет 20% и 500%.
С ростом ставки дисконта чистая

приведенная стоимость сначала растет, а затем снижается. Причина этого заключается в том, что знак потоков денежных средств дважды меняется. Может быть столько различных значений внутренней нормы доходности проекта, сколько раз изменяется знак потоков денежных средств.

Слайд 126 Внутренняя норма доходности
Заблуждение 3. Фирмам часто приходится выбирать

Внутренняя норма доходностиЗаблуждение 3. Фирмам часто приходится выбирать один из нескольких

один из нескольких альтернативных способов выполнения одной и той

же работы или использования одних и тех же мощностей. Говоря другими словами, им необходимо сделать выбор из взаимоисключающих проектов. И в этом случае использование критерия внутренней нормы доходности также может привести к ошибке.

Слайд 127 Внутренняя норма доходности
Рассмотрим проекты D и E:

Внутренняя норма доходностиРассмотрим проекты D и E:

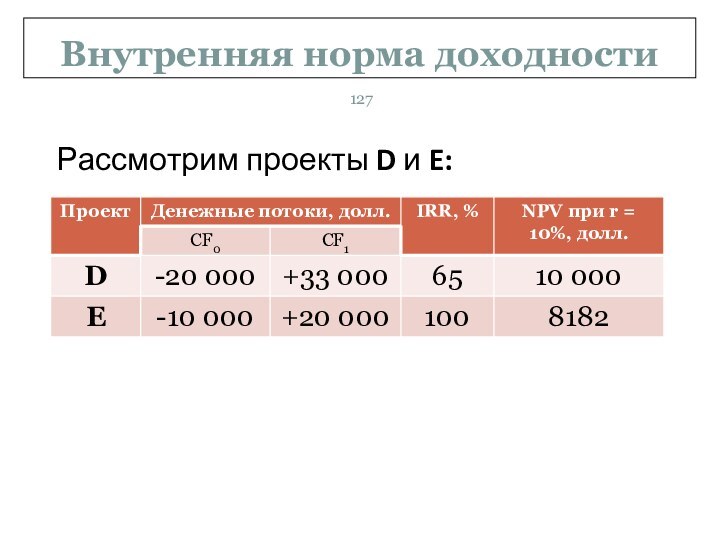
Слайд 128 Внутренняя норма доходности
Оба проекта представляют собой хорошие варианты

Внутренняя норма доходностиОба проекта представляют собой хорошие варианты инвестирования, но проект

инвестирования, но проект D имеет более высокую чистую приведенную

стоимость и, следовательно, является лучшим. Если же инвестор ориентируется на критерий внутренней нормы доходности, то он должен выбрать проект Е, поскольку он имеет более высокую внутреннюю норму доходности.

Слайд 129 Внутренняя норма доходности
Если инвестор будет руководствоваться методом внутренней

Внутренняя норма доходностиЕсли инвестор будет руководствоваться методом внутренней нормы доходности, его

нормы доходности, его удовлетворит норма доходности в 100%; если

же он будет следовать методу чистой приведенной стоимости, он станет богаче на 10 000 долл.

Слайд 130 Внутренняя норма доходности
В таких случаях рекомендуется использовать метод

Внутренняя норма доходностиВ таких случаях рекомендуется использовать метод внутренней нормы доходности

внутренней нормы доходности для оценки внутренней нормы доходности приростных

потоков. Как это сделать?
Во-первых, инвестор должен рассмотреть проект меньшей стоимости (в нашем примере это проект Е). Его внутренняя норма доходности равна 100% и превосходит альтернативные издержки, равные 10%. Следовательно, проект Е приемлем.

Слайд 131 Внутренняя норма доходности
Во-вторых, инвестор решает стоит ли инвестировать

Внутренняя норма доходностиВо-вторых, инвестор решает стоит ли инвестировать дополнительно 10 000

дополнительно 10 000 дол. в проект D. Осуществление проекта

D по сравнению с проектом Е дает следующие приросты потоков денежных средств:

Слайд 132 Внутренняя норма доходности
Внутренняя норма доходности дополнительных инвестиций равна

Внутренняя норма доходностиВнутренняя норма доходности дополнительных инвестиций равна 30%, что также

30%, что также значительно превышает 10%-ные альтернативные издержки. Поэтому

инвестору следует отдать предпочтение проекту D.
Если бы величина внутренней нормы доходности дополнительных инвестиций оказалась бы ниже значения альтернативных издержек, то тогда инвестору следует реализовать проект Е.

Слайд 133 Внутренняя норма доходности
Без рассмотрения приростных вложений внутренняя норма

Внутренняя норма доходностиБез рассмотрения приростных вложений внутренняя норма доходности не может

доходности не может служить надежным критерием для ранжирования проектов

различных масштабов. Он также ненадежен при выборе проектов с различным распределением денежных потоков во времени.

Слайд 134 Внутренняя норма доходности
Для иллюстрации такого подхода рассмотрим пример,

Внутренняя норма доходностиДля иллюстрации такого подхода рассмотрим пример, в котором денежные

в котором денежные потоки по проектам представлены в таблице

ниже.

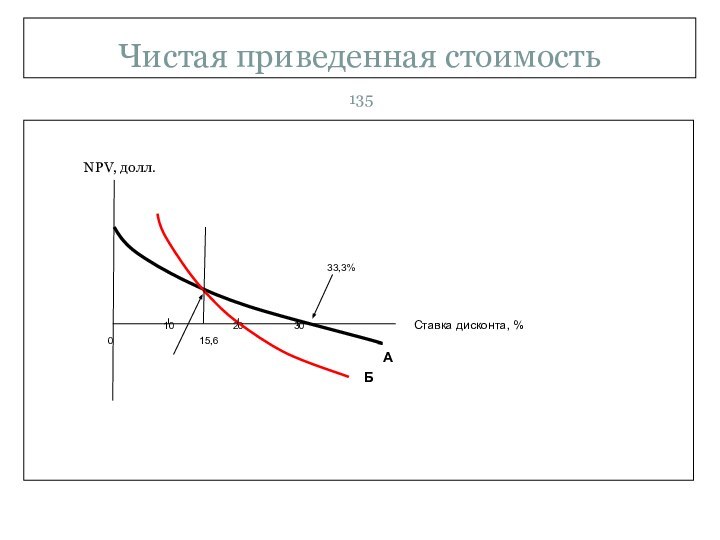
Слайд 135 Чистая приведенная стоимость

Чистая приведенная стоимость NPV, долл.

NPV, долл.






33,3%



10 20 30 Ставка дисконта, %
0 15,6
А
Б

Слайд 136 Чистая приведенная стоимость
Проект А имеет более высокую внутреннюю

Чистая приведенная стоимостьПроект А имеет более высокую внутреннюю норму доходности, но

норму доходности, но у проекта Б выше чистая приведенная

стоимость. На рисунке ниже показано, почему два метода приводят к разным результатам.

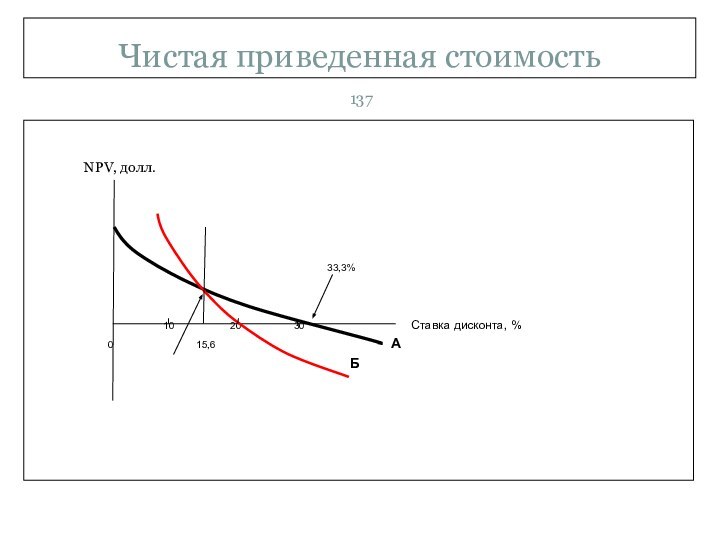
Слайд 137 Чистая приведенная стоимость

Чистая приведенная стоимость NPV, долл.

NPV, долл.






33,3%



10 20 30 Ставка дисконта, %
0 15,6 А
Б

Слайд 138 Чистая приведенная стоимость
Чёрная линия обозначает чистую приведенную стоимость

Чистая приведенная стоимостьЧёрная линия обозначает чистую приведенную стоимость проекта А при

проекта А при различных ставках дисконта. Так как при

ставке дисконта, равной 33%, чистая приведенная стоимость равна нулю, то она выступает внутренней нормой доходности проекта А.

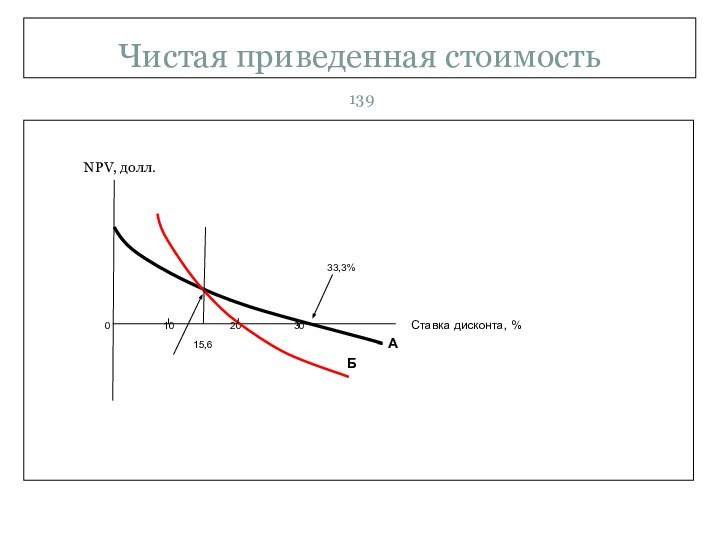
Слайд 139 Чистая приведенная стоимость

Чистая приведенная стоимость NPV, долл.

NPV, долл.






33,3%



0 10 20 30 Ставка дисконта, %
15,6 А
Б

Слайд 140 Чистая приведенная стоимость
Аналогично, красная линия обозначает чистую приведенную

Чистая приведенная стоимостьАналогично, красная линия обозначает чистую приведенную стоимость проекта Б

стоимость проекта Б при различных ставках дисконта. Внутренняя норма

доходности проекта Б равна 20%. Заметим, что проект Б имеет более высокую чистую приведенную стоимость до тех пор, пока альтернативные издержки составляют менее 15,6%.

Слайд 141 Чистая приведенная стоимость
Причина, по которой метод внутренней нормы

Чистая приведенная стоимостьПричина, по которой метод внутренней нормы доходности ведёт к

доходности ведёт к ошибочным заключениям, состоите том, что хотя

совокупный приток денежных средств по проекту Б более крупный, однако возникает он позже. Поэтому, когда ставка дисконта низкая, проект Б имеет более высокую чистую приведенную стоимость; когда ставка дисконта высокая, более высокую чистую приведенную стоимость имеет проект А.

Слайд 142 Чистая приведенная стоимость
Если посмотреть на внутренние нормы доходности

Чистая приведенная стоимостьЕсли посмотреть на внутренние нормы доходности двух проектов, то

двух проектов, то заметим, что при ставке дисконта 20%

чистая приведенная стоимость проекта Б равна нулю (внутренняя норма доходности равна 20%), а чистая приведенная стоимость проекта А положительна. Таким образом, если бы альтернативные издержки составляли 20%, инвесторы могли бы более высоко оценить краткосрочный проект А.

Слайд 143 Чистая приведенная стоимость
В рассматриваемом примере альтернативные издержки равны

Чистая приведенная стоимостьВ рассматриваемом примере альтернативные издержки равны не 20%, а

не 20%, а 10%. Инвесторы готовы заплатить относительно более

высокую цену за долгосрочные ценные бумаги, и поэтому они заплатят относительно высокую цену за долгосрочный проект. При альтернативных издержках, равных 10%, чистая приведенная стоимость инвестиций в проект Б составляет 8406 долл., а инвестиций в проект А только 3592 долл.

Слайд 144 Чистая приведенная стоимость
Если фирма сталкивается с ограничениями на

Чистая приведенная стоимостьЕсли фирма сталкивается с ограничениями на капитал, либо объективные,

капитал, либо объективные, либо специально установленные, использовать внутреннюю норму

доходности в качестве критерия отбора проектов нельзя. В этом случае задача сводится к тому, чтобы отыскать такой пакет инвестиционных проектов, который отвечал бы ограничениям на капитал и имел наибольшую чистую приведенную стоимость.

Слайд 145 Чистая приведенная стоимость
С помощью метода внутренней нормы доходности

Чистая приведенная стоимостьС помощью метода внутренней нормы доходности такой пакет определить

такой пакет определить невозможно. Обычно на практике для этого

используют метод линейного программирования.

Слайд 146 Чистая приведенная стоимость
Внутренняя норма доходности дополнительных инвестиций в

Чистая приведенная стоимостьВнутренняя норма доходности дополнительных инвестиций в проект Б равна

проект Б равна 15,6%. Поскольку она превышает альтернативные издержки,

проект Б и следует принять. Когда приходится выбирать между проектами А и Б, наиболее лёгкий способ - сравнить чистые приведенные стоимости.

Слайд 147 Чистая приведенная стоимость
Применение коэффициента рентабельности может привести к

Чистая приведенная стоимостьПрименение коэффициента рентабельности может привести к ошибкам, когда мы

ошибкам, когда мы должны выбрать между двумя взаимоисключающими инвестиционными

проектами. Рассмотрим два следующих проекта D и E:

Слайд 148 Чистая приведенная стоимость
Коэффициент рентабельности инвестиций указывает, что оба

Чистая приведенная стоимостьКоэффициент рентабельности инвестиций указывает, что оба проекта хороши. Но

проекта хороши. Но если предположить, что проекты D и

E взаимоисключающие, то инвестор должен. принять проект Е — проект с более высокой чистой приведенной стоимостью. Тем не менее, если судить по коэффициенту рентабельности инвестиций, приоритет принадлежит проекту D.

Слайд 149 Чистая приведенная стоимость
Как и в случае с внутренней

Чистая приведенная стоимостьКак и в случае с внутренней нормой доходности, инвестор

нормой доходности, инвестор всегда можем решить эту проблему, рассмотрев

коэффициент рентабельности приростных инвестиций. Говоря иначе, сначала удостоверьтесь, что проект D стоит осуществить, затем рассчитывается коэффициент рентабельности 9900 дол. дополнительных инвестиций в проект Е:

Слайд 150 Чистая приведенная стоимость
В этом случае рентабельность дополнительных инвестиций

Чистая приведенная стоимостьВ этом случае рентабельность дополнительных инвестиций будет равна 1,36,

будет равна 1,36, и, следовательно, следует принять проект Е,

поскольку рассматриваемый коэффициент больше единицы.

Слайд 151 Чистая приведенная стоимость
Мы рассмотрели несколько критериев оценки эффективности

Чистая приведенная стоимостьМы рассмотрели несколько критериев оценки эффективности инвестиционных проектов. Для

инвестиционных проектов. Для большинства целей показатель чистая приведенная стоимость

, который обладает свойством аддитивности, служит более надежным критерием, чем коэффициент рентабельности инвестиций, не обладающий таким свойством.

Слайд 152 Чистая приведенная стоимость
Анализ чувствительности - систематический способ анализа,

Чистая приведенная стоимостьАнализ чувствительности - систематический способ анализа, при котором определяются

при котором определяются факторы, влияющие на денежный поток, и

оценивается степень влияния каждого из факторов. Цель анализа состоит в том, чтобы оценить, как "чувствительна" чистая приведенная стоимость к изменениям ряда экономических факторов:

Слайд 153 Учет риска при оценке капиталовложений
a) вычисляются числовые оценки

Учет риска при оценке капиталовложенийa) вычисляются числовые оценки зависимых переменных (NPV

зависимых переменных (NPV или IRR) относительно экономических переменных (например,

цена на электричество);
б) оценивается степень неопределенности переменных, имеющих большее воздействие.

Слайд 154 Учет риска при оценке капиталовложений
Пример. Денежные потоки, получаемые

Учет риска при оценке капиталовложенийПример. Денежные потоки, получаемые в результате реализации

в результате реализации проекта по выработке электричества показаны в

табл. 1, представленной ниже. Дисконтная ставка для приведения будущих денежных потоков к текущему периоду принимается равной 11 %.

Слайд 155 Учет риска при оценке капиталовложений

Учет риска при оценке капиталовложений

Слайд 156 Учет риска при оценке капиталовложений
Определим экономические показатели, получаемые

Учет риска при оценке капиталовложенийОпределим экономические показатели, получаемые при реализации проекта.1.

при реализации проекта.
1. Валовая выручка = (цена) × (выработанная

мощность) =
= 2,5 руб./кВт × 1000000 кВт = 2500000 руб./год.
2. Налогооблагаемая прибыль = валовая выручка–издержки–амортизация =
= 2500000 - 500000 – 1000000 = 1000000 руб./год.

Слайд 157 Учет риска при оценке капиталовложений
3. Налог на прибыль

Учет риска при оценке капиталовложений3. Налог на прибыль = (ставка налога

= (ставка налога на прибыль)× (налогооблагаемая прибыль) = 0,2

× 1000000 = 200000 руб./год.
4. Чистая прибыль = (налогооблагаемая прибыль) – (налог на прибыль) =
= 1000000 – 200000 = 800000 руб./год.
5. Чистые денежные потоки = (чистая прибыль) + (амортизация) =
= 800000 + 1000000 = 1800000 руб./год.

Слайд 158 Учет риска при оценке капиталовложений
6. Приведенная величина будущих

Учет риска при оценке капиталовложений6. Приведенная величина будущих денежных потоков определяется

денежных потоков определяется по формуле:

5,8892×1800000=10 600 560 руб.

7. NPV = PV –I =
= 10 600 560 – 10 000 000 = 600 560 руб.
Учитывая результаты расчетов, показывающие положительную величину NPV проекта, можно рекомендовать данный проект к реализации.



Слайд 159 Учет риска при оценке капиталовложений
Оценим чувствительность показателя NPV

Учет риска при оценке капиталовложенийОценим чувствительность показателя NPV к ошибке в

к ошибке в 10 % в экономических факторах, затрагивающих

денежные потоки. Чтобы сделать это, необходимо определить величины NPV, используя пересмотренные значения каждого отдельно взятого фактора (табл. 2).

Слайд 160 Учет риска при оценке капиталовложений Таблица 2

Учет риска при оценке капиталовложений Таблица 2

Слайд 161 Учет риска при оценке капиталовложений
Из данных табл. 2

Учет риска при оценке капиталовложенийИз данных табл. 2 можно сделать вывод,

можно сделать вывод, что показатель NPV наиболее чувствителен к

ошибкам в прогнозах цены электричества и объема вырабатываемой мощности. Если прогнозы изменяются на 10 % в неправильном направлении, NPV проекта изменяется от положительного значения 600 560 руб. до отрицательного (-577 280 руб.). Расчеты показывают, что показатель NPV также довольно чувствителен к ошибкам в сроке жизни проекта.

Слайд 162 Учет риска при оценке капиталовложений
При дискретном распределении вероятности

Учет риска при оценке капиталовложенийПри дискретном распределении вероятности значений денежных потоков

значений денежных потоков математическое ожидание денежного потока равно

, (2)

где CFt – величина денежного потока в период t, руб.; pt – вероятность возникновения денежного потока в период t, доли ед.

Слайд 163 Учет риска при оценке капиталовложений
Коэффициент вариации CV вероятностного

Учет риска при оценке капиталовложенийКоэффициент вариации CV вероятностного распределения определяется следующим

распределения определяется следующим образом:

(3)

Слайд 164 Учет риска при оценке капиталовложений
Среднеквадратическое отклонение служит мерой

Учет риска при оценке капиталовложенийСреднеквадратическое отклонение служит мерой неопределенности величины денежного

неопределенности величины денежного потока и измеряется в тех же

единицах, что и ожидаемое значение денежного потока. Коэффициент вариации обеспечивает относительную меру неопределенности, которая может быть выражена в процентах.

Слайд 165 Учет риска при оценке капиталовложений
Пример 8.17. Предположим, что

Учет риска при оценке капиталовложенийПример 8.17. Предположим, что среднеквадратическое отклонение наличного

среднеквадратическое отклонение наличного потока A и наличного потока В

равно 50000 руб. Также предположим, что ожидаемое значение денежного потока А равно 100000 руб., тогда как ожидаемое значение денежного потока В равно 1000000 руб.

Слайд 166 Учет риска при оценке капиталовложений
Тогда показатель CV для

Учет риска при оценке капиталовложенийТогда показатель CV для А равен 0,5

А равен 0,5 или 50 %, а значение СV

для потока В будет равно 0,05 или 5 %. Для практических целей, денежный поток B обладает большей степенью определенности в сравнении с денежным потоком А, поскольку поток А характеризуется высокой степенью неопределенности. Это различие в неопределенности выражается коэффициентом вариации, а не стандартным отклонением.

Слайд 167 Учет риска при оценке капиталовложений

Учет риска при оценке капиталовложений

Слайд 168 Учет риска при оценке капиталовложений

Учет риска при оценке капиталовложений

Слайд 169 Чистая приведенная стоимость

Чистая приведенная стоимость

Слайд 170 Чистая приведенная стоимость

Чистая приведенная стоимость

Слайд 171 Чистая приведенная стоимость

Чистая приведенная стоимость

Слайд 172 Чистая приведенная стоимость

Чистая приведенная стоимость

Слайд 173 Чистая приведенная стоимость

Чистая приведенная стоимость

Слайд 174 Чистая приведенная стоимость

Чистая приведенная стоимость

Слайд 175 Чистая приведенная стоимость

Чистая приведенная стоимость

Слайд 176 Чистая приведенная стоимость

Чистая приведенная стоимость

Слайд 177 Чистая приведенная стоимость

Чистая приведенная стоимость

Слайд 178 Чистая приведенная стоимость

Чистая приведенная стоимость

Слайд 179 Чистая приведенная стоимость

Чистая приведенная стоимость

Слайд 180 Чистая приведенная стоимость

Чистая приведенная стоимость

Слайд 181 Чистая приведенная стоимость

Чистая приведенная стоимость

Слайд 182 Чистая приведенная стоимость

Чистая приведенная стоимость

Слайд 183 Чистая приведенная стоимость

Чистая приведенная стоимость

Слайд 184 Чистая приведенная стоимость

Чистая приведенная стоимость

Слайд 185 Чистая приведенная стоимость

Чистая приведенная стоимость

Слайд 186 Чистая приведенная стоимость

Чистая приведенная стоимость

Слайд 187 Чистая приведенная стоимость

Чистая приведенная стоимость

Слайд 188 Чистая приведенная стоимость

Чистая приведенная стоимость

Слайд 189 Чистая приведенная стоимость

Чистая приведенная стоимость

Слайд 190 Чистая приведенная стоимость

Чистая приведенная стоимость

Слайд 191 Чистая приведенная стоимость

Чистая приведенная стоимость

Слайд 192 Чистая приведенная стоимость

Чистая приведенная стоимость

Слайд 193 Чистая приведенная стоимость

Чистая приведенная стоимость

Слайд 194 Чистая приведенная стоимость

Чистая приведенная стоимость

Слайд 195 Чистая приведенная стоимость

Чистая приведенная стоимость

Слайд 196 Чистая приведенная стоимость

Чистая приведенная стоимость

Слайд 197 Чистая приведенная стоимость

Чистая приведенная стоимость

Слайд 198 Чистая приведенная стоимость

Чистая приведенная стоимость

Слайд 199 Чистая приведенная стоимость

Чистая приведенная стоимость

Слайд 200 Чистая приведенная стоимость

Чистая приведенная стоимость

Слайд 201 Чистая приведенная стоимость

Чистая приведенная стоимость

Слайд 202 Чистая приведенная стоимость

Чистая приведенная стоимость

Слайд 203 Чистая приведенная стоимость

Чистая приведенная стоимость

Слайд 204 Чистая приведенная стоимость

Чистая приведенная стоимость

Слайд 205 Чистая приведенная стоимость

Чистая приведенная стоимость

Слайд 206 Чистая приведенная стоимость

Чистая приведенная стоимость

Слайд 207 Чистая приведенная стоимость

Чистая приведенная стоимость

Слайд 208 Чистая приведенная стоимость

Чистая приведенная стоимость

Слайд 209 Чистая приведенная стоимость

Чистая приведенная стоимость

Слайд 210 Чистая приведенная стоимость

Чистая приведенная стоимость

Слайд 211 Чистая приведенная стоимость

Чистая приведенная стоимость

Слайд 212 Чистая приведенная стоимость

Чистая приведенная стоимость

Слайд 213 Чистая приведенная стоимость

Чистая приведенная стоимость

Слайд 214 Чистая приведенная стоимость

Чистая приведенная стоимость

Слайд 215 Чистая приведенная стоимость

Чистая приведенная стоимость

Слайд 216 Чистая приведенная стоимость

Чистая приведенная стоимость

Слайд 217 Чистая приведенная стоимость

Чистая приведенная стоимость

Слайд 218 Чистая приведенная стоимость

Чистая приведенная стоимость

Слайд 219 Чистая приведенная стоимость

Чистая приведенная стоимость

Слайд 220 Чистая приведенная стоимость

Чистая приведенная стоимость

Слайд 221 Чистая приведенная стоимость

Чистая приведенная стоимость

Слайд 222 Чистая приведенная стоимость

Чистая приведенная стоимость

Слайд 223 Чистая приведенная стоимость

Чистая приведенная стоимость

Слайд 224 Чистая приведенная стоимость

Чистая приведенная стоимость

Слайд 225 Чистая приведенная стоимость

Чистая приведенная стоимость

Слайд 226 Чистая приведенная стоимость

Чистая приведенная стоимость

Слайд 227 Чистая приведенная стоимость

Чистая приведенная стоимость

Слайд 228 Чистая приведенная стоимость

Чистая приведенная стоимость

Слайд 229 Чистая приведенная стоимость

Чистая приведенная стоимость

Слайд 230 Чистая приведенная стоимость

Чистая приведенная стоимость

Слайд 231 Чистая приведенная стоимость

Чистая приведенная стоимость

Слайд 232 Чистая приведенная стоимость

Чистая приведенная стоимость

Слайд 233 Чистая приведенная стоимость

Чистая приведенная стоимость

Слайд 234 Чистая приведенная стоимость

Чистая приведенная стоимость

Слайд 235 Чистая приведенная стоимость

Чистая приведенная стоимость

Слайд 236 Чистая приведенная стоимость

Чистая приведенная стоимость

Слайд 237 Чистая приведенная стоимость

Чистая приведенная стоимость

Слайд 238 Чистая приведенная стоимость

Чистая приведенная стоимость

Слайд 239 Чистая приведенная стоимость

Чистая приведенная стоимость

Слайд 240 Чистая приведенная стоимость

Чистая приведенная стоимость
  • Имя файла: chistaya-privedennaya-stoimost.pptx
  • Количество просмотров: 163
  • Количество скачиваний: 0
- Предыдущая Инструментальная детекция лжи
Следующая - Богатство и своеобразие культуры Древней Руси

Похожие презентации

Современные методы лечения хронической сердечной недостаточности Современные методы лечения хронической сердечной недостаточности 88
Презентация для классного часа на тему Выбор молодых: государственное управление в XXI веке Презентация для классного часа на тему Выбор молодых: государственное управление в XXI веке 125
Западный и Восточный типы культуры Западный и Восточный типы культуры 116
Загадочный планетарий Загадочный планетарий 150
Презентация по ПМ01 ЭиТО для професии 35.01.13 на тему Тесты по устройству трактора и автомобиля Презентация по ПМ01 ЭиТО для професии 35.01.13 на тему Тесты по устройству трактора и автомобиля 107
разработка сети широкополосного доступа в селе Нылга, Увинского района по технологии GPON разработка сети широкополосного доступа в селе Нылга, Увинского района по технологии GPON 89
Easter Easter 109
Теория развития критического мышления методическая разработка (1, 2, 3, 4 класс) Теория развития критического мышления методическая разработка (1, 2, 3, 4 класс) 95
ispolzovanie slov raznyh grupp v rechi ispolzovanie slov raznyh grupp v rechi 137
Урок-проект выполненный учащимися 11 класса по теме:Возможен ли мир без курения Урок-проект выполненный учащимися 11 класса по теме:Возможен ли мир без курения 123
Психологические особенности детей 5-6 лет презентация к уроку (старшая группа) Психологические особенности детей 5-6 лет презентация к уроку (старшая группа) 85
Современные детские конструкторы презентация по теме Современные детские конструкторы презентация по теме 57
prezentatsiya microsoft powerpoint 2 prezentatsiya microsoft powerpoint 2 92
Презентация к родительскому собранию: Спайс Презентация к родительскому собранию: Спайс 109
Дедуктивные умозаключения Дедуктивные умозаключения 105
1 сентября 2015 1 сентября 2015 122
Отличительныечерты windows 8.1 Отличительныечерты windows 8.1 101
Презентация Субъективная сторона преступления Презентация Субъективная сторона преступления 138
Презентация по географии на тему Рождество и Святки Презентация по географии на тему Рождество и Святки 105
Axalta coating systemsЦветовая поддержка dupont refinishВстреча дистрибьюторов10/04/2013 Axalta coating systemsЦветовая поддержка dupont refinishВстреча дистрибьюторов10/04/2013 79
§ Плоскость1. Общее уравнение плоскости § Плоскость1. Общее уравнение плоскости 102
Картотека опытов по детскому экспериментированию опыты и эксперименты (старшая группа) Картотека опытов по детскому экспериментированию опыты и эксперименты (старшая группа) 158
Город возможностей. Правила игры Город возможностей. Правила игры 103
Тайны паркетов Тайны паркетов 104
Тема: Вторичный документальны поток как составная часть информационных ресурсов по направлению подготовки Сервис и Туризм. Тема: Вторичный документальны поток как составная часть информационных ресурсов по направлению подготовки Сервис и Туризм. 117
ДИДАКТИЧЕСКАЯ ИГРА КАК СРЕДСТВО РАЗВИТИЯ РЕЧИ презентация по теме ДИДАКТИЧЕСКАЯ ИГРА КАК СРЕДСТВО РАЗВИТИЯ РЕЧИ презентация по теме 115
Шаблоны презентаций Новогодние 9 Шаблоны презентаций Новогодние 9 98
Современные горочная техника концерна ТРАНСМАШ Современные горочная техника концерна ТРАНСМАШ 112
Эфирные масла.Ароматерапия Эфирные масла.Ароматерапия 73
Презентация по теме: Компетентностно-ориентированные задания: содержание, структура,возможности использования в пространстве урока. презентация к уроку по теме Презентация по теме: Компетентностно-ориентированные задания: содержание, структура,возможности использования в пространстве урока. презентация к уроку по теме 139