Презентация на тему Астрономические системы отсчета и методы их построения

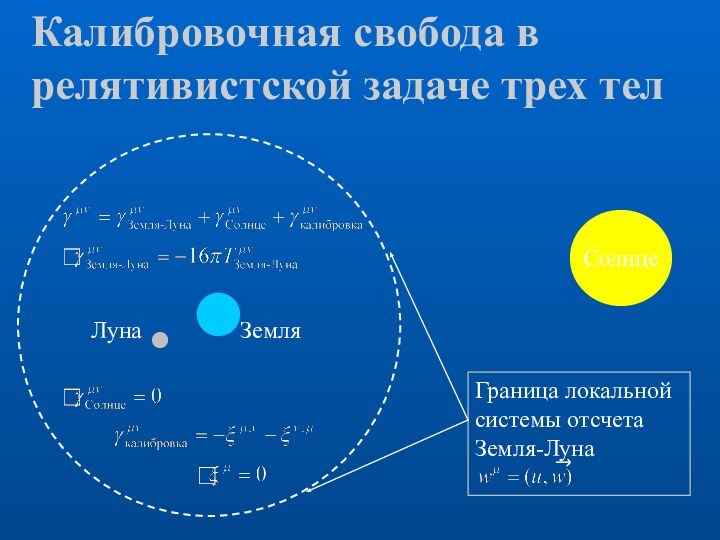
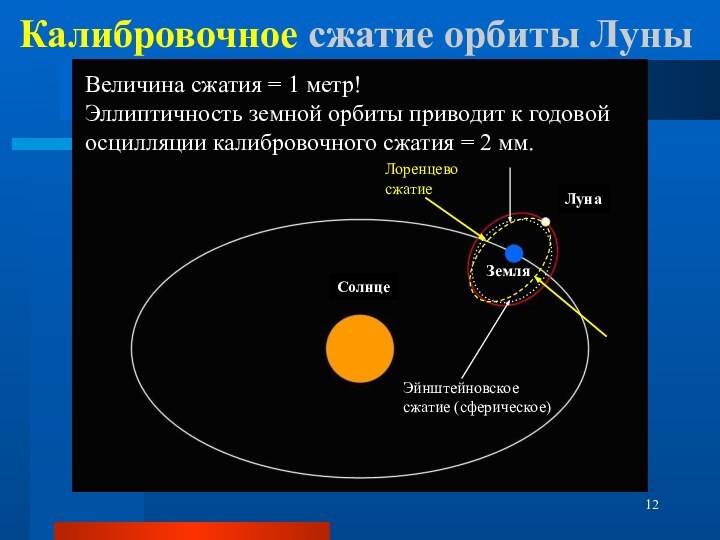
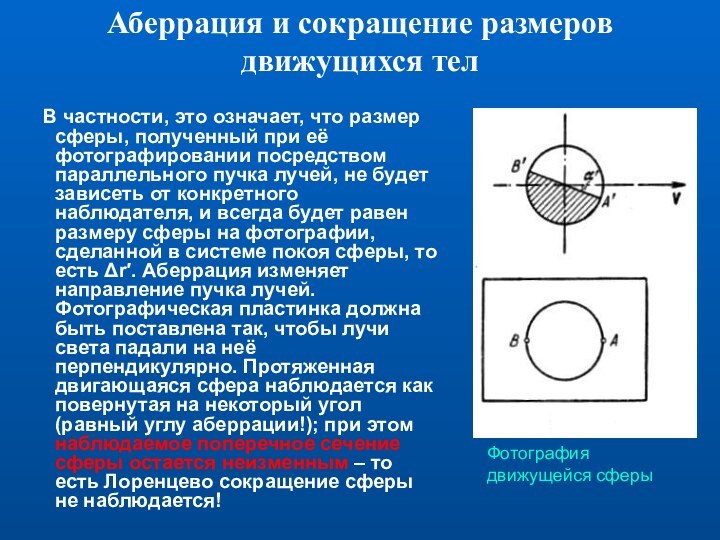
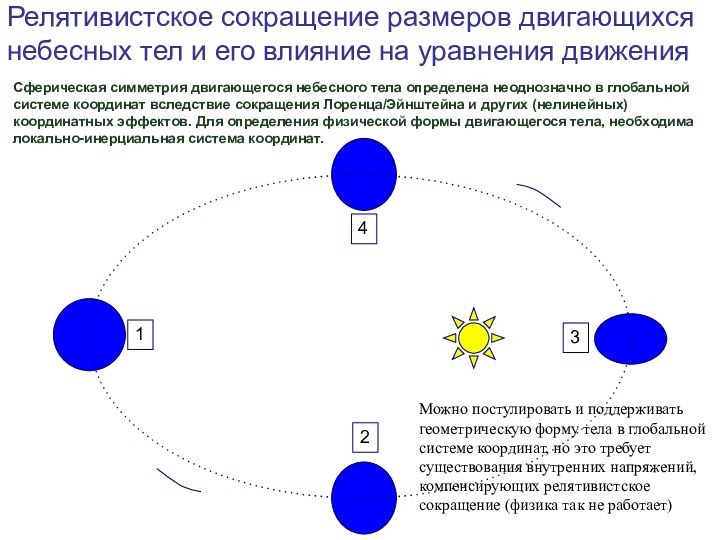
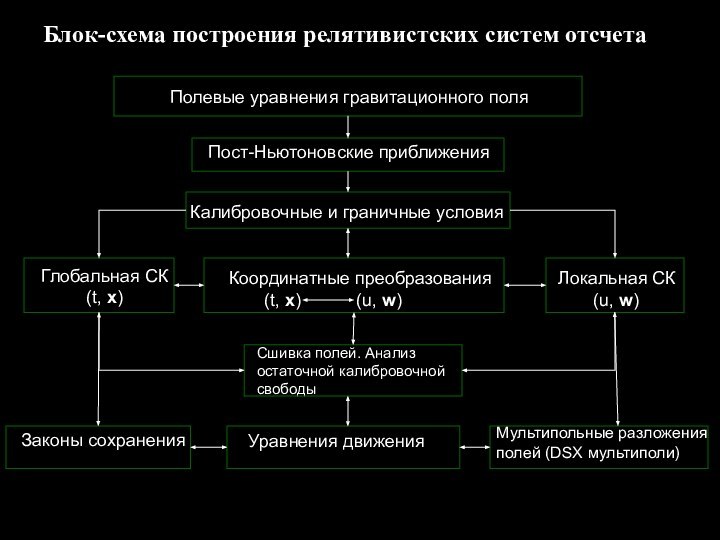
свобода
Мультипольные гравитационные поля
Пост-Ньютоновские приближения
Асимптотические сшивки полей
Теория систем отсчета: резолюции

МАС 2000
Теория прецессии и нутации МАС 2000
Компьютерные коды: NASA GEODYNE, Orbit Determination Program, CALC VLBI, etc.

Устраняет нефизические степени свободы из наблюдаемых величин
Адекватная интерпретация гравитационных

экспериментов
Параметризованный пост-Ньютоновский (ППН) формализм – морально устарел, требует модернизации. Причина:
Нединамичен
Системы отсчета не разработаны
Нековариантен
Калибровочные степени свободы перепутаны с физическими эффектами
Не вполне адекватен в интерпретации гравитационной физики и тестов ОТО

калибровочно-зависимые решения и эффекты

инвариантность эл.-эм. поля

кривизны

Эйнштейна

«Остаточная» калибровочная свобода

системы отсчета
Земля-Луна

Эйнштейновское сжатие



Релятивистская прецессия (de Sitter, Lense-Thirring, Thomas)

Эллиптичность земной орбиты приводит к годовой
осцилляции калибровочного сжатия

= 2 мм.

Земля

Лоренцево
сжатие

Эйнштейновское
сжатие (сферическое)

Солнце

Луна

отсутствуют в наблюдаемых данных, не имеют отношения к физическим

эффектам
Нордведт: да – отсутствуют в наблюдаемых данных, их отсутствие указывает на присутствие гравимагнитного поля (эффект «голого короля»)
Kopeikin, S., Phys. Rev. Lett., vol. 98, id. 229001 (2007)
The LLR technique involves processing data with two sets of mathematical equations, one related to the motion of the moon around the earth, and the other related to the propagation of the laser beam from earth to the moon. These equations can be written in different ways based on "gauge freedom," the idea that arbitrary coordinates can be used to describe gravitational physics. The gauge freedom of the LLR technique shows that the manipulation of the mathematical equations is causing JPL scientists to derive results that are not apparent in the data itself.

В частности, это означает, что размер

сферы, полученный при её фотографировании посредством параллельного пучка лучей, не будет зависеть от конкретного наблюдателя, и всегда будет равен размеру сферы на фотографии, сделанной в системе покоя сферы, то есть r. Аберрация изменяет направление пучка лучей. Фотографическая пластинка должна быть поставлена так, чтобы лучи света падали на неё перпендикулярно. Протяженная двигающаяся сфера наблюдается как повернутая на некоторый угол (равный углу аберрации!); при этом наблюдаемое поперечное сечение сферы остается неизменным – то есть Лоренцево сокращение сферы не наблюдается!

Фотография
движущейся сферы

Земля-Луна:
“Ньютоновские” преобразования релятивистской гравитационной 4-х силы



Устраняет все калибровочные степени

свободы из преобразований координат!
Переводит все калибровочные степени свободы в уравнения движения Луны вокруг Земли, где они появляются как фиктивные (ненаблюдаемые) силы

глобальной системе координат вследствие сокращения Лоренца/Эйнштейна и других (нелинейных)

координатных эффектов. Для определения физической формы двигающегося тела, необходима локально-инерциальная система координат.

Можно постулировать и поддерживать
геометрическую форму тела в глобальной
системе координат, но это требует
существования внутренних напряжений,
компенсирующих релятивистское
сокращение (физика так не работает)

Релятивистское сокращение размеров двигающихся небесных тел и его влияние на уравнения движения

координат приводит к появлению фиктивной пост-Ньютоновской силы (Брумберг 1972;

Копейкин и Власов 2004)

роль, но трудна для конкретного понимания
Неправильное истолкование калибровочной свободы

влечет:
появление нефизических эффектов в уравнениях движения;
неправильной интерпретации наблюдаемых данных;
предложение ошибочных гравитационных экспериментов;
нефизическую трактовку прецесии и нутации, неправильным выводам о внутренней структуре Земли и Луны;
неточностям в построении навигационных систем и геодезических координатных сетей;
ошибкам в прецезионной космической навигации в ближнем и дальнем космосе
Внимательно изучаем труды классиков и осваиваем тонкости теорий, обладающих калибровочной свободой

приближения
Калибровочные и граничные условия
Глобальная СК

(t, x)

Локальная СК
(u, w)

Координатные преобразования
(t, x) (u, w)

Сшивка полей. Анализ
остаточной калибровочной
свободы

Законы сохранения

Уравнения движения

Мультипольные разложения
полей (DSX мультиполи)