Презентация на тему Движение в гравитационном поле. Исскуственные спутники Земли

Солнечная система

Гравитация внутри Земли

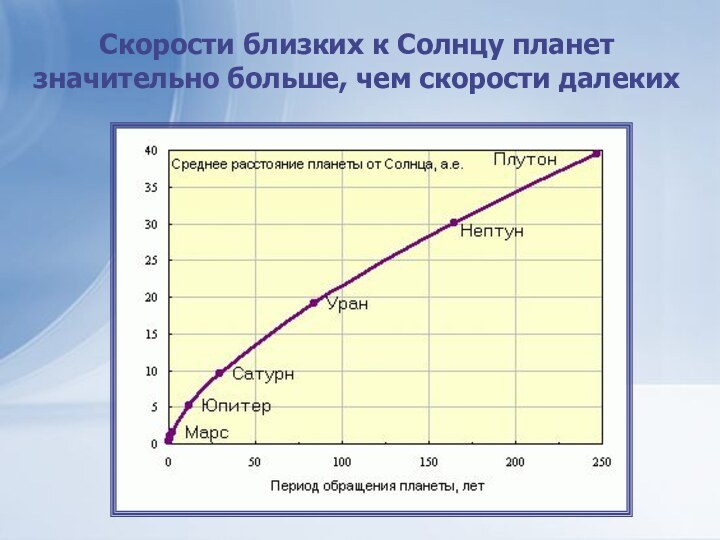
Законы Кеплера

Движение спутников

Элементы орбиты спутника

Межпланетный перелет

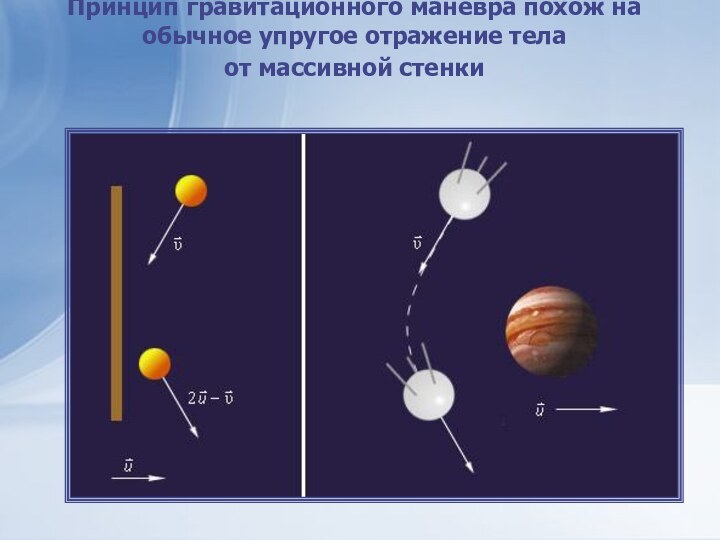
Гравитационный маневр

происхождением, упорядоченностью движения и общностью физических свойств. Центральным телом

Солнечной системы является Солнце. Вокруг него по эллиптическим орбитам вращаются девять больших планет.

Солнечная система

своей оси.

планетам земной группы, состоящим, в основном, из скалистых и

металлических пород и имеющим небольшие размеры, относятся Меркурий, Венера, Земля и Марс.

Характеристики планет

расположены дальше от Солнца; их металлические ядра окутывает плотная

атмосфера из водорода, гелия и других газов.

Характеристики планет

Характеристики планет

малые планеты (астероиды), составляющие два пояса; один из них

находится между орбитами Марса и Юпитера, а второй – пояс Койпера, – за орбитой Нептуна. В настоящее время полагают, что Плутон является одним из объектов пояса Койпера. Далеко за поясом Койпера находится еще одно пылевое облако – облако Оорта. Кроме того, в Солнечную систему входят многочисленные кометы, облетающие Солнце по сильно вытянутым орбитам, межпланетная пыль и газ.

размеры больших планет, но и расстояния от большинства спутников

до планет. Радиус Солнца в 109 раз, а масса – в 330 000 раз больше радиуса и массы Земли.

пространстве с помощью закона всемирного тяготения. Ньютон пришел к

своей теории в результате многолетних исследований движения Луны и планет

Ускорение, которое испытывает тело m, находящееся на расстоянии r от тела M, равно

Вблизи поверхности Земли ускорение свободного падения равно g = 9,8 м/с2. Сплюснутость Земли и ее вращение приводят к отличию силы тяжести на экваторе и возле полюсов: ускорение свободного падения в точке наблюдения может приближенно высчитываться по формуле g = 9,78 ∙ (1 + 0,0053 sin φ), где φ – широта этой точки.

сила тяжести убывает пропорционально расстоянию до центра:
Модель показывает,

как изменяется сила тяжести внутри Земли. Из теоремы Гаусса следует, что если считать Землю однородным шаром, сила тяжести внутри ее уменьшается пропорционально расстоянию до центра. Слева изображена Земля (ее правая половина показана в разрезе так, что виден туннель, проходящий на расстоянии L от центра; это расстояние можно менять). В правом нижнем углу изображен график зависимости ускорения свободного падения от расстояния до центра Земли. Серая линия отмечает радиус Земли, равный 6371 км. При нажатии кнопки Старт в туннель начинает падать тело. Силы трения, а также вращение Земли в модели не учитываются. Тело летит к центру туннеля под действием силы тяжести.

Пройдя середину тоннеля на максимальной скорости, оно начинает замедляться. Достигнув противоположной точки туннеля, тело останавливается и начинает падать обратно, совершая таким образом колебательные движения. График зависимости ускорения тела от времени приведен справа вверху. Движение тела можно приостановить или прекратить при помощи кнопок Стоп и Сброс.

поднимается и снижается, причем в устьях некоторых рек и

отдельных заливах на несколько метров. Эти явления носят название приливов и отливов. Гидросфера, как и всякое жидкое тело, способна деформироваться, что и происходит каждый день в результате притяжения Луны и Солнца. Луна каждые 24 часа 50 минут вызывает приливы не только в океанах, но и в коре Земли, и в атмосфере. Под воздействием приливных сил литосфера вытягивается примерно на полметра.

движение в гравитационном поле определяется законом сохранения энергии, то

есть K + U = сonst, где – кинетическая энергия тела массой m, движущегося со скоростью υ,  – потенциальная энергия этого тела, находящегося на расстоянии r от тела массой M. Константа h называется постоянной энергии.

коническому сечению
В 1679 году Исаак Ньютон показал, что любое тело

в поле тяготения будет двигаться по коническому сечению онические сечения образуются при пересечении прямого кругового конуса с плоскостью. К коническим сечениям относятся кривые второго порядка: эллипс, парабола и гипербола, а также пара параллельных прямых. Все они является геометрическим местом точек, отношение расстояний от которых до заданной точки (фокуса) и до заданной прямой (директрисы) есть величина постоянная, равная эксцентриситету e. При e < 1 получается эллипс, при e = 1 – парабола, при e > 1 – гипербола.

сумма расстояний от двух заданных точек (фокусов F1 и

F2) есть величина постоянная и равная длине большой оси: r1 + r2 = |AA´| = 2a. Степень вытянутости эллипса характеризуется его эксцентриситетом e. Эксцентриситет e = OF/OA. При совпадении фокусов с центром e = 0, и эллипс превращается в окружность.
Большая полуось a является средним расстоянием от фокуса (планеты от Солнца): a = (AF1 + F1A')/2.

движения спутника Земли. Запуск модели производится кнопкой Старт, приостановка

и возвращение в исходное состояние – кнопками Стоп и Сброс соответственно. Группа переключателей Закон позволяет выбрать, какой закон Кеплера будет в настоящий момент иллюстрироваться.
В центре окна вращается Земля. Вокруг нее по орбите движется спутник. Параметры орбиты (расстояние до Земли в перигее и начальную скорость) можно задать при помощи окон ввода в нижней части модели. В информационном окне приводятся прочие параметры орбиты: длина большой и малой полуосей, эксцентриситет и период обращения, а также виртуальное текущее время.
Первый закон Кеплера показывает, что все планеты движутся по эллипсу. Изменением начальной скорости небесного тела вы можете превратить эллиптическую орбиту в гиперболическую: по гиперболическим орбитам мимо Солнца движутся некоторые кометы и ряд спутников, покидающих пределы Солнечной системы.

Второй закон Кеплера показывает равенство площадей, заметаемых радиус–вектором небесного тела за равные промежутки времени. При этом скорость тела меняется в зависимости от расстояния до Земли (особенно хорошо это заметно, если тело движется по сильно вытянутой эллиптической орбите).
Демонстрация третьего закона Кеплера осуществляется при помощи двух спутников. В этом режиме можно задать параметры орбиты каждого спутника. Сравнив периоды обращения и радиусы орбит спутников, можно убедиться в справедливости закона.

скорости далеких

спутника в гравитационном поле Земли. На схеме изображены вращающаяся

Земля и спутник, двигающийся вокруг нее по эллиптической или гиперболической орбите согласно законам Кеплера. Параметры орбиты (начальную скорость, начальное расстояние и направление начальной скорости спутника) можно задать в окнах ввода. Если спутник подойдет слишком близко к Земле, он останавливается.
В информационном окне показаны тип орбиты, период обращения и виртуальное текущее время. Кнопки Старт, Стоп и Сброс позволяют управлять анимацией, запуская и приостанавливая модель и возвращая ее к исходному состоянию.

от того, в каком направлении корабль выходит из зоны

действия земного тяготения

вокруг Земли

для описания положения искусственных спутников Земли, – систему орбитальных

элементов. Шесть элементов определяют положение и наклон орбиты относительно земного экватора, размеры орбиты и положение спутника на ней. Ось OX направлена на точку весеннего равноденствия.
Если выключатель, соответствующий объекту системы, не выбран, этот объект отображается серым цветом. Если же его выбрать, то объект окрасится ярким цветом, а на схеме появится его название.

с космического аппарата за короткое время можно увидеть большую

часть поверхности земного шара.

круговых орбит импульсами, направленными «по скорости» и «против скорости».

Как видно из схем, орбита испытывает наибольшее геометрическое смещение в области, противолежащей точке, в которой телу был сообщен импульс

перелетов.
Нажмите на кнопку Старт. Ракета, обращающаяся вместе с Землей,

включит двигатели и выйдет на промежуточную эллиптическую орбиту (эллипс Гомана). При достижении афелия двигатели включаются еще раз, и космический аппарат перейдет на орбиту Марса. Время старта должно быть точно рассчитано, чтобы в тот момент, когда межпланетная станция перейдет на марсианскую орбиту, планета оказалась в том же месте.

Кнопки Стоп и Сброс приостанавливают модель и возвращают ее в исходное состояние. Если выбрать теперь при помощи соответствующего переключателя перелет с Марса на Землю, все произойдет в обратном порядке: находясь на орбите Марса, аппарат получит импульс торможения и перейдет на промежуточную эллиптическую орбиту; второй импульс торможения в перигелии промежуточной орбиты переведет его на орбиту Земли.

зависит от того, в какой точке орбиты он выполняется

маневр космического аппарата в поле тяжести планеты с целью

увеличения собственной скорости аппарата.
В центре модели на фоне звездного неба показано небесное тело, в гравитационном поле которого производится маневр. Его можно выбрать из списка Планеты (можно выбрать Солнце, Луну и 9 больших планет Солнечной системы).
Модель запускается кнопкой Старт. При этом справа на прицельном расстоянии с начальной скоростью v0 начинает двигаться космический аппарат. Пролетая мимо планеты, он разворачивается на угол φ (его значение можно посмотреть в информационном окне) или сталкивается с поверхностью планеты (если прицельное расстояние или начальная скорость слишком малы). При помощи окон ввода Начальная скорость и Прицельное расстояние можно менять параметры движения космического аппарата, а кнопки Стоп и Сброс приостанавливают анимацию и возвращают модель к исходному состоянию.

Помимо разворота космического корабля, маневр может использоваться для увеличения его собственной скорости. Этот эффект сходен с эффектом увеличения скорости шарика после удара с массивной упругой стенкой, движущейся ему навстречу. Если скорость шарика до удара была v, а стенки –u, то после удара шарик приобретает скорость 2u + v (это становится ясным, если перейти в систему отсчета, связанную со стенкой). Спутник же увеличивает свою скорость, когда разворачивается вокруг планеты, двигающейся ему навстречу.