Слайд 2
Как определить расстояние от Земли до Солнца?
Зная расстояние
между двумя наблюдателями и угол, под которым они видят
Солнце, можно вычислить расстояние от Земли до Солнца. Оно составляет 1,496 108 км и называется астрономической единицей.
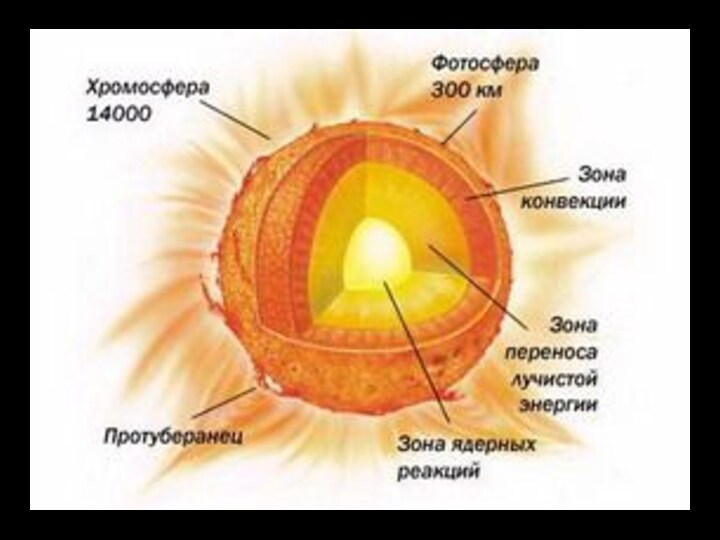
Как определить радиус Солнца?
Размеры Солнца известны с той же точностью, что и астрономическая единица, так как размеры определяют путём умножения углового диаметра Солнца (0,5о) на астрономическую единицу. Определённая таким способом величина диаметра Солнца составляет 1393000 км, что примерно в 108 раз больше диаметра Земли.
Слайд 3
Как определить массу Солнца?
Пусть Мз – масса Земли,
Rз – радиус Земли, m – масса яблока (упавшего
на голову Ньютона). На яблоко, лежащее на земле, действует сила притяжения Земли, которую нужно приравнять весу яблока mg.
GMзm/Rз2=mg ? G=gRз2/Mз
Учитывая, что Mз=ρ(4/3)πRз3 имеем G=3gRз2/(4ρπRз3)=3g/(4πρRз). При Rз=6,37 106 м, ρ=5 103 кг/м3 имеем G=7,35 10-11 н м2 кг-2. Это, вычисленное Ньютоном, значение гравитационной постоянной, лишь на 10% превышает принятое значение G=6,67 10-11 н м2 кг-2.
Слайд 4
Скорость движения тела по окружности равна длине окружности,
делённой на период обращения:
V=2πR/T
где R – расстояние между Солнцем
и Землёй, T – период обращения Земли вокруг Солнца (1 год). Приравнивая силу притяжения Земли к Солнцу к центробежной силе, действующей на Землю при её движении по круговой орбите, вычисляем массу Солнца:
GMсMз/R2=MзV2/R ? GMсMз/R2=Mз(4π2R/T2) ? Mс=4π2R3/(GT2)
По современным данным Mс=1,99 1033 г и в 333000 раз больше массы Земли. В Солнце сосредоточено 99,866% массы солнечной системы.
Ускорение свободного падения на поверхности Солнца gc = GMс/Rс = 2,74 104 см/сек2.
Слайд 5
Как определить температуру на поверхности Солнца?
Понятие температуры имеет
реальное значение только в условиях термодинамического равновесия. Хотя условия
на Солнце не вполне отвечают термодинамическому равновесию, фотосфера излучает энергию, как если бы она была абсолютно чёрным телом. Если сравнить кривую распределения энергии в спектре с малым разрешением для фотосферы с кривой излучения для чёрного тела, то эти кривые лучше всего совпадают при температуре около 6000 К (λmax × T = const – закон смещения Вина) . Кривые расходятся только для очень коротких и для очень длинных волн.
Слайд 6
Как оценить температуру в центре Солнца?
Давление внутри Солнца
на глубине h равно P=ρh, где - среднее
ускорение свободного падения внутри Солнца. В модели однородного шара постоянной плотности гравитационное поле линейно возрастает по мере перехода от центра шара к его поверхности. Поэтому =(1/2) GMс/Rс и в центре Солнца (h=Rc) имеем P=(1/2)ρGMс/Rс. Если Солнце – это шар идеального водородного газа, то согласно уравнению состояния идеального газа давление в центре Солнца P=ρkT/mp, где mp – масса протона, k – постоянная Больцмана. Приравнивая эти два выражения для давления в центре Солнца получаем оценку температуры в центре Солнца:
T=GMcmp/(2kRc)~107 K
Слайд 8
Почему Солнце светит?
При температурах ~ 107 K водород
в центральных частях Солнца полностью ионизован (потенциал ионизации водорода
13,6 эв, 1 эв = 11600 К) и ведёт себя необычно. Дело в том, что при слиянии лёгких ядер (например, двух ядер атома водорода), также как и при делении тяжёлых ядер, получаются более прочные (более устойчивые) ядра (с большей взаимосвязанностью нуклонов), чем исходные. Поэтому при слиянии лёгких ядер избыточная энергия должна выделяться.
Слияние ядер может произойти только в том случае, когда две тяжёлые частицы, одной из которых обычно бывает протон, сталкиваются друг с другом с относительной скоростью, достаточной для того, чтобы преодолеть электростатические силы их взаимного отталкивания, и сближаются настолько, что начинают проявляться силы ядерного взаимодействия. Чем больше заряды ядер, тем большей энергией должны обладать частицы, чтобы вступить в ядерную реакцию.
Слайд 9
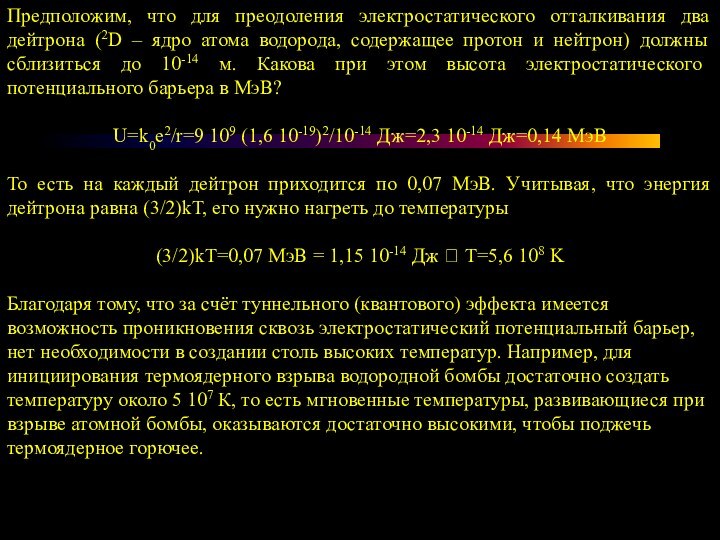
Предположим, что для преодоления электростатического отталкивания два дейтрона
(2D – ядро атома водорода, содержащее протон и нейтрон)
должны сблизиться до 10-14 м. Какова при этом высота электростатического потенциального барьера в МэВ?
U=k0e2/r=9 109 (1,6 10-19)2/10-14 Дж=2,3 10-14 Дж=0,14 МэВ
То есть на каждый дейтрон приходится по 0,07 МэВ. Учитывая, что энергия дейтрона равна (3/2)kT, его нужно нагреть до температуры
(3/2)kT=0,07 МэВ = 1,15 10-14 Дж ? T=5,6 108 K
Благодаря тому, что за счёт туннельного (квантового) эффекта имеется возможность проникновения сквозь электростатический потенциальный барьер, нет необходимости в создании столь высоких температур. Например, для инициирования термоядерного взрыва водородной бомбы достаточно создать температуру около 5 107 К, то есть мгновенные температуры, развивающиеся при взрыве атомной бомбы, оказываются достаточно высокими, чтобы поджечь термоядерное горючее.
Слайд 10
Ядерные реакции, требующие для своего осуществления температур порядка

миллиона градусов, называются термоядерными. На Солнце они могут протекать
лишь в самых горячих его областях (~ 107 К) и, как правило, между ядрами, заряды которых не больше 7 (ядра азота). Кроме того, частота столкновений может быть значительной лишь при достаточно высокой плотности вещества, то есть в центральной части Солнца.
Водород может превращаться в гелий в центральной части Солнца несколькими путями. Первый путь – водородный цикл - реализует следующая цепочка реакций:
p + p ? 2D + e+ + νe + 1,44 МэВ 99,75%
(p + e- + p ? 2D + νe 0,25%)
2D + p ? 3He + γ + 5,49 МэВ 100%
3He + 3He ? 4He + p + p + 12,85 МэВ 85%
Верхние индексы означают число протонов плюс нейтронов в ядре. В отличие от полной энергии кинетическая энергия взаимодействующих частиц не сохраняется (за исключением процесса упругого рассеяния). Разность между суммарной кинетической энергией частиц – продуктов реакции и суммарной кинетической энергией частиц, вступающих в реакцию, называется энергией реакции. Энергия реакции может быть положительной (энергия реакции освобождается за счёт уменьшения энергии покоя, а значит и массы, частиц в процессе реакции) или отрицательной (кинетическая энергия бомбардирующей частицы должна превышать некий порог).
Слайд 11
Вначале сталкиваются два протона, образуя дейтрон, позитрон и

нейтрино (эта реакция представляет собой пример слабого взаимодействия и
аналогична превращению протона в радиоактивном ядре в нейтрон и пару электрон-нейтрино – один из видов бета-распада. Принято считать, что радиус действия слабых сил много меньше радиуса действия ядерных сил. Нейтрино может участвовать только в слабом взаимодействии. Поэтому любой процесс с участием нейтрино обязательно слабый, то есть идёт медленно, и наоборот в сильном и электромагнитном процессе не может возникнуть или поглотиться нейтрино. Аналогично, гамма-квант может участвовать только в электромагнитном взаимодействии). Позитрон вскоре аннигилирует с электроном, их исчезновение сопровождается испусканием гамма-лучей.
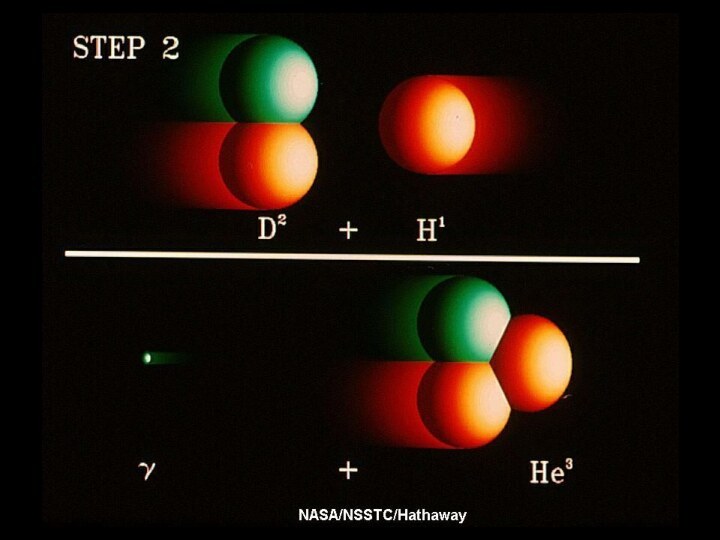
Во второй реакции дейтрон сливается с протоном, образуя 3He; при этом испускается гамма-излучение.
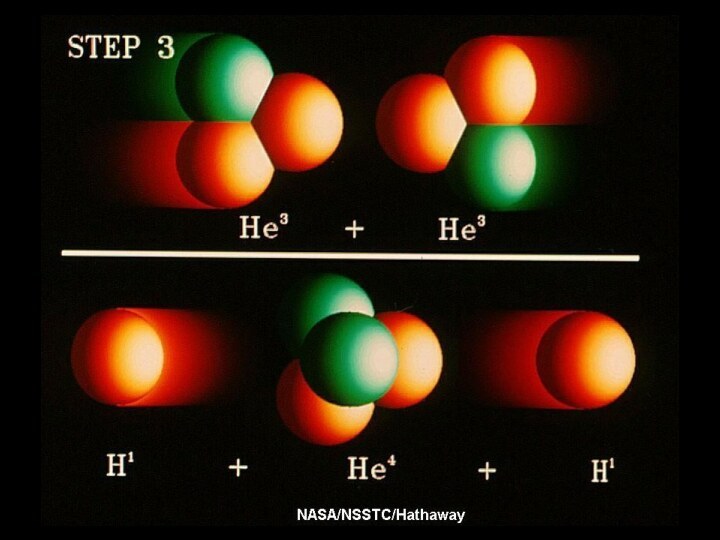
Третий шаг – образование 4He может произойти в различных реакциях; здесь приведена наиболее вероятная. На этом шаге возможны также ещё два сценария:
3He + 4He ? 7Be + γ
7Be + e- ? 7Li + νe
7Li + p ? 4He + 4He
7Be + p ? 8Be + γ
8Be ? 4He + e+ + νe
Слайд 12
Суммарная реакция этой цепочки представляет собой слияние четырёх
протонов с образованием одного ядра гелия (альфа-частицы), двух электронных
нейтрино и двух гамма-квантов. Энергетический выход цепочки составляет 26,7 Мэв, из которых нейтрино уносят по 0,26 МэВ каждое, так что остаётся 26,2 МэВ.
Четыре ядра атома водорода (mH=1,0081 а.е.м.) объединяются в ядро атома гелия (mHe=4,0039 а.е.м.). Результирующее ядро имеет меньшую массу, чем сумма масс первоначальных ядер и эта очень маленькая разность масс высвобождается при протекании ядерных реакций в виде очень большой энергии нейтрино и гамма-квантов.
Первая из реакций водородного цикла протекает медленее остальных и именно она определяет скорость, с которой осуществляется вся цепочка.
Слайд 16
Второй возможный механизм превращения водорода в гелий –

углеродный цикл – предложен одновременно и независимо Гансом Бете
и Карлом фон Вейцзеккером (оба они активные участники германского уранового проекта 1938-44 гг). Он складывается из следующих реакций, в которых углерод действует как катализатор:
12C + p ? 13N + γ + 1,95 МэВ
13N ? 13C + e+ + νe + 2,22 МэВ
13С + p ? 14N + γ + 7,54 МэВ
14N + p ? 15O + γ + 7,35 МэВ
15O ? 15N + e+ + νe + 2,71 МэВ
15N + p ? 12C + 4He + γ + 4,96 МэВ
Конечный результат этой последовательности реакций точно такой же, как и у цепочки водородного цикла, только в этом случае нейтрино уносят в среднем по 1,7 МэВ и на каждое образовавшееся ядро 4He приходится 24 МэВ освобождённой энергии гамма излучения.
Поскольку для преодоления кулоновского потенциального барьера 14N протону требуется большее количество энергии, чем для взаимодействия с другим протоном, углеродный цикл осуществляется при более высокой температуре (однако, располагая достаточным количеством энергии, протон реагирует с 14N гораздо охотнее, чем с другим протоном).
Слайд 17
Таким образом, в центральной части сферы с радиусом

в одну четвёртую часть радиуса Солнца – в ядре
Солнца (то есть в 1/64 объёма Солнца) генерируется 99% солнечной энергии.
Как проверить термоядерную концепцию экспериментально?
До недавнего времени представлялось, что исследование внутренних областей Солнца будет сводиться к построению теоретических моделей. Казалось, что совершенно невозможно заглянуть под поверхность Солнца. Первым прорывом в этом направлении оказалась нейтринная астрономия Солнца. Из центральной области Солнца до его поверхности электромагнитное излучение из-за многократного рассеяния, поглощения и переизлучения доходит за время около 1 млн. лет, при этом его спектр существенно изменяется: гамма-излучение превращается в видимый свет (в 200 раз больший путь от Солнца до Земли свет проходит всего за 8 мин). В отличие от фотонов, солнечные нейтрино, возникающие в результате ядерных реакций в центре Солнца, доходят до нас практически не поглощаясь. Зная полную светимость Солнца можно теоретически оценить ожидаемый интегральный поток солнечных нейтрино на орбите Земли. При этом измерение потока солнечных нейтрино является единственной экспериментальной возможностью проверить наши представления об источнике энергии Солнца.
Слайд 19
Нейтрино – частица, которая испытывает только слабое взаимодействие

(характерные сечения в диапазоне спектра солнечных нейтрино σ=10-42–10-43 см2).
Поэтому ожидаемое количество взаимодействий на 1 атом мишени мало σФ=10-32 – 10-36 сек-1. (Поток солнечных нейтрино принято измерять в солнечных нейтринных единицах Solar Neutrino Unit: 1 SNU=10-36 сек-1 – количество взаимодействий за 1 сек на 1036 атомов мишени). Очевидно, что для регистрации даже единичных нейтрино требуются уникальные технологии, гигантские мишени и длительные периоды наблюдений.
Полное число частиц, участвующих в столкновениях, δN пропорционально числу падающих частиц N, толщине мишени δx и средней плотности n частиц в единице объёма мишени. Коэффициент пропорциональности σ, вообще говоря зависящий от энергии падающих на мишень частиц, называется сечением.
Существуют два способа регистрации нейтрино:
Нейтрино может быть захвачено ядром мишени в реакции обратного К захвата (n + νe ? p + e-)
Нейтрино может быть рассеяно электроном мишени (e + νx ? e’ + νx’, аналог рассеяния Комптона) или ядром мишени с последующим его распадом (например, дейтроном 2D + νx ? n + p + νx)
Слайд 20
Непосредственно регистрируются образовавшиеся радиоактивные ядра (радиохимические детекторы) или
черенковский свет от вторичных заряженных частиц (черенковские детекторы). Благодаря
узкой направленности черенковского излучения при рассеянии нейтрино на электроне можно определить направление прихода нейтрино. Отметим, что на электронах и ядрах могут рассеиваться нейтрино различных типов, хотя эффективные сечения рассеяния для неэлектронных нейтрино значительно меньше. Поэтому черенковские детекторы регистрируют нейтрино всех типов, но с различной эффективностью.
Первым способом (радиохимические детекторы) регистрация мюонных нейтрино с энергией значительно меньше массы мюона запрещена законом сохранения энергии.
Слайд 21
Измерения потока солнечных нейтрино показали, что:
- В

углеродном цикле генерируется менее 9% солнечной энергии.
- Верхний предел
измеренного потока солнечных нейтрино оказался по крайней мере в 2-3 раза ниже, чем предсказывают современные теоретические модели. Результат этих измерений указывает на какую-то фундаментальную ошибку в наших представлениях о недрах Солнца. Эта «загадка солнечных нейтрино» может иметь астрофизические (ошибки стандартной модели Солнца) или ядернофизические (незнание физики нейтрино) причины. Исследовались следующие возможные источники ошибок: 1) начальное содержание гелия в протосолнечном веществе было меньше, чем 0,16-0,20 2) в значениях одного или нескольких эффективных поперечных сечений ядер содержатся неожиданно большие ошибки 3) значительно завышены оценки одного или нескольких эффективных поперечных сечений для поглощения нейтрино 4) Солнце было вначале неоднородным и осталось в дальнейшем таким же 5) в течение фазы ядерного горения в недрах Солнца происходило значительное перемешивание 6) возраст Солнца существенно меньше 4,5 109 лет 7) в недрах Солнца существуют сильные крупномасштабные магнитные поля, напряжённость которых вблизи центра достигает 109 Гс 8) гравитационная постоянная возрастает со временем.
Слайд 22
Сколько водорода сгорает на Солнце в 1 сек?
Если
W – мощность солнечного излучения, поглощаемая каждым квадратным метром
земной атмосферы (солнечная постоянная), то энергия, выделяемая на Солнце в 1 сек, равна
E=4πR2W
где R – расстояние от Земли до Солнца. Этой, выделяемой в единицу времени, энергии соответствует масса
M=E/c2.
Реакция образования ядра атома гелия (mHe=4,0039 а.е.м.) из четырёх ядер атомов водорода (mH=1,0081 а.е.м.) заключается в том, что четыре ядра водорода объединяются в ядро гелия. Хотя при этом образуются две частицы с массой покоя, отличной от нуля, они в дальнейшем также превращаются в излучение (позитроны, встречаясь с электронами, «пропадают», образуя гамма-кванты). Поэтому можно утверждать, что часть массы водорода
K=(4mH-mHe)/4mH = 7,1 10-3
отвечает энергии, выделившейся в результате реакции синтеза. Таким образом, в 1 секунду на Солнце «сгорает» масса водорода
m=M/K=4πR2W/(Kc2)=6,25 108 тонн,
что составляет примерно 3 10-17% массы Солнца.