Презентация на тему КУРС АСТОРОМИИ

без которой невозможно решение всех остальных задач астрономии, является

определение положения небесного светила на небесной сфере.
Небесная сфера - это воображаемая сфера произвольного радиуса, описанная из глаза наблюдателя, как из центра. На эту сферу мы проектируем положение всех небесных светил. Расстояния на небесной сфере можно измерять только в угловых единицах, в градусах, минутах, секундах или радианах. Например, угловые диаметры Луны и Солнца равны примерно 0.5°.

положение наблюдаемого небесного светила, является отвесная линия.
Плоскость, перпендикулярная

отвесной линии, называется горизонтальной плоскостью.

В каждой точке Земли наблюдатель видит половину сферы, плавно вращающейся с востока на запад вместе с будто прикрепленными к ней звездами. Это видимое вращение небесной сферы объясняется равномерным вращением Земли вокруг своей оси с запада на восток.
Отвесная линия пересекает небесную сферу в точке зенита, Z и в точке надира, Z'.

Большой круг небесной сферы, по которому горизонтальная плоскость, проходящая через глаз наблюдателя (точка С на рис.2), пересекается с небесной сферой, называется истинным горизонтом. Напомним, что большим кругом небесной сферы является круг, проходящий через центр небесной сферы. Круги, образованные пересечением небесной сферы с плоскостями, не проходящими через ее центр, называются малыми кругами. Линия, параллельная земной оси и проходящая через центр небесной сферы, называется осью мира. Она пересекает небесную сферу в северном полюсе мира, P, и в южном полюсе мира P'.

Большой круг небесной сферы, плоскость которого перпендикулярна оси мира, называется небесным экватором. Небесный экватор делит небесную сферу на две части: северную и южную. Небесный экватор параллелен экватору Земли.

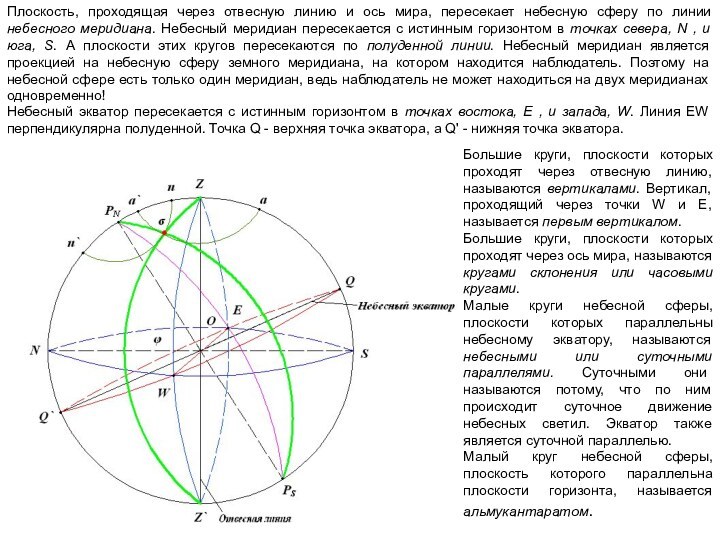
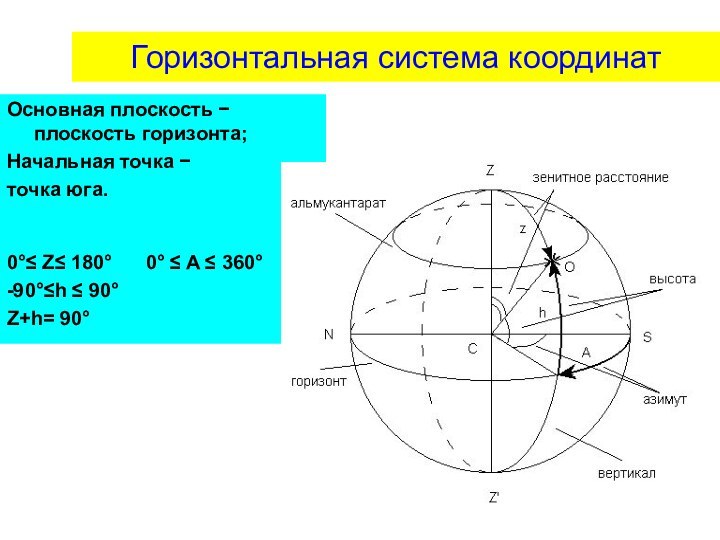
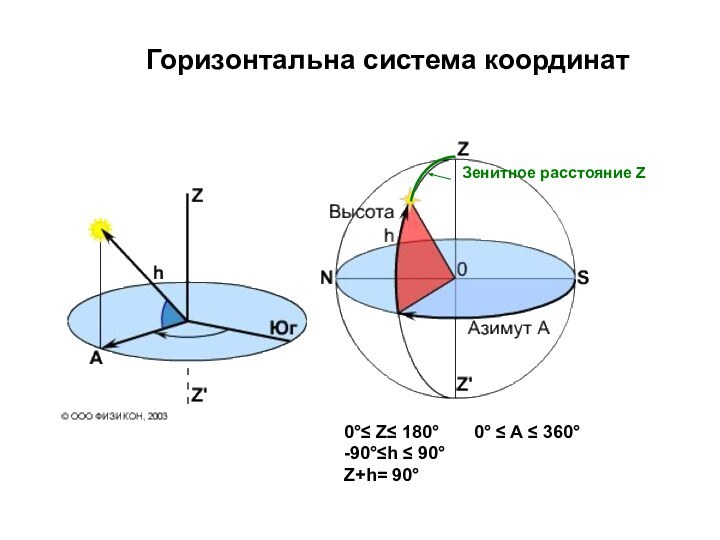
называются вертикалами. Вертикал, проходящий через точки W и E,

называется первым вертикалом.
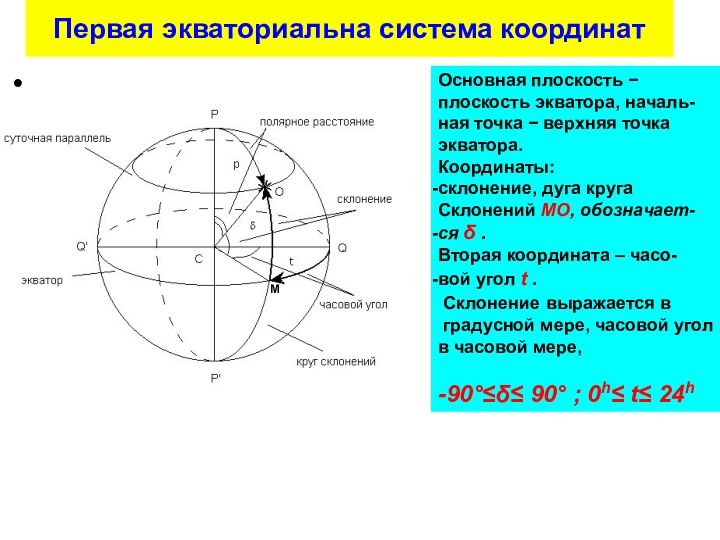
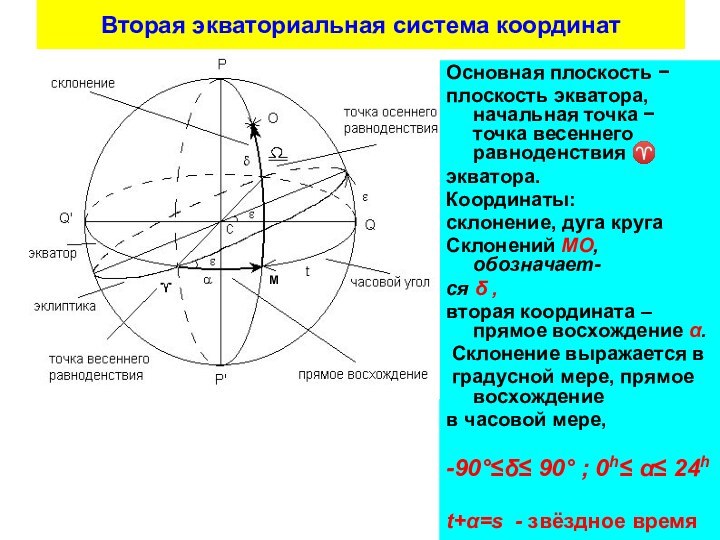
Большие круги, плоскости которых проходят через ось мира, называются кругами склонения или часовыми кругами.
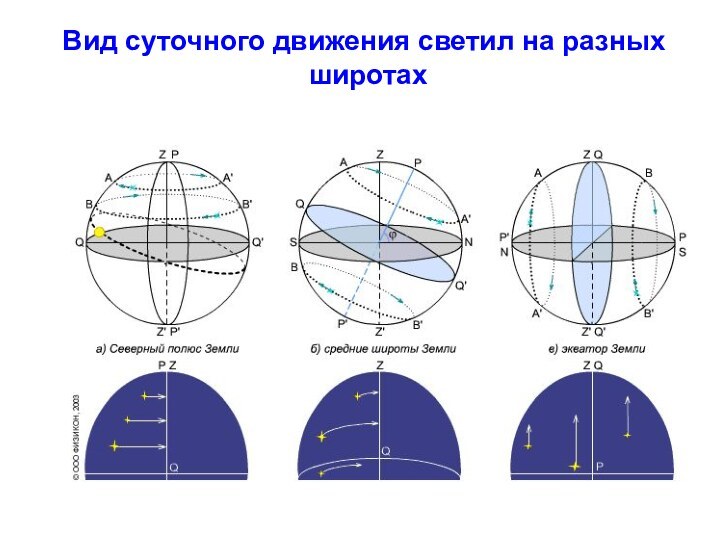
Малые круги небесной сферы, плоскости которых параллельны небесному экватору, называются небесными или суточными параллелями. Суточными они называются потому, что по ним происходит суточное движение небесных светил. Экватор также является суточной параллелью.
Малый круг небесной сферы, плоскость которого параллельна плоскости горизонта, называется альмукантаратом.

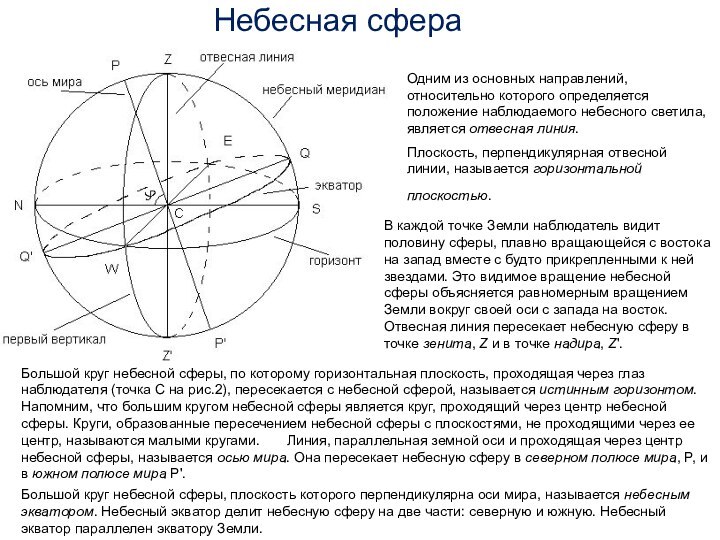
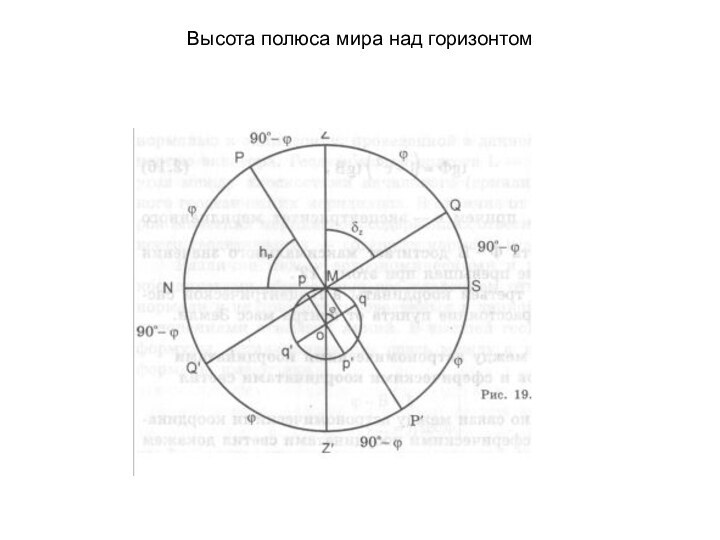
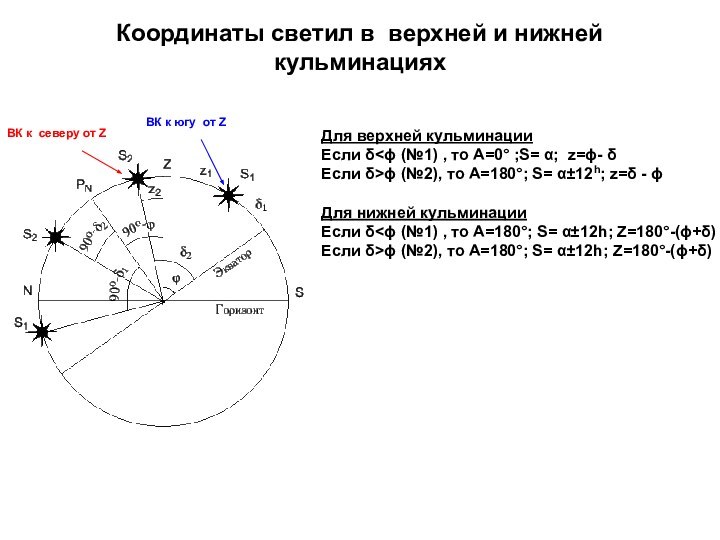
Небесный экватор пересекается с истинным горизонтом в точках востока, E , и запада, W. Линия EW перпендикулярна полуденной. Точка Q - верхняя точка экватора, а Q' - нижняя точка экватора.

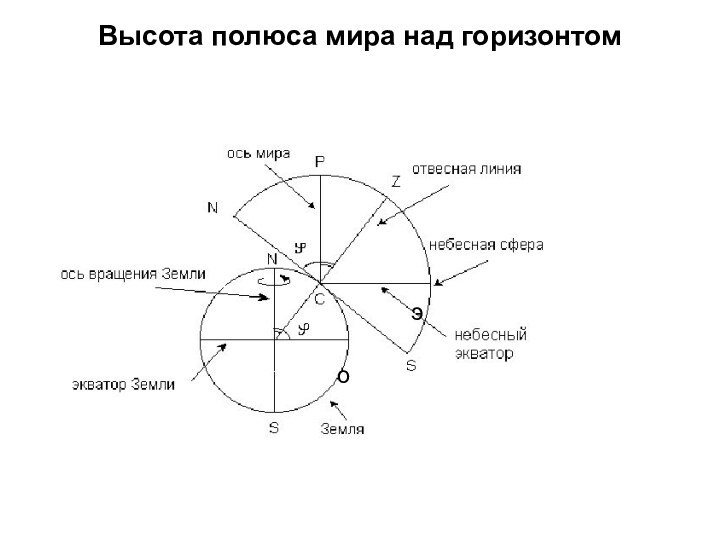
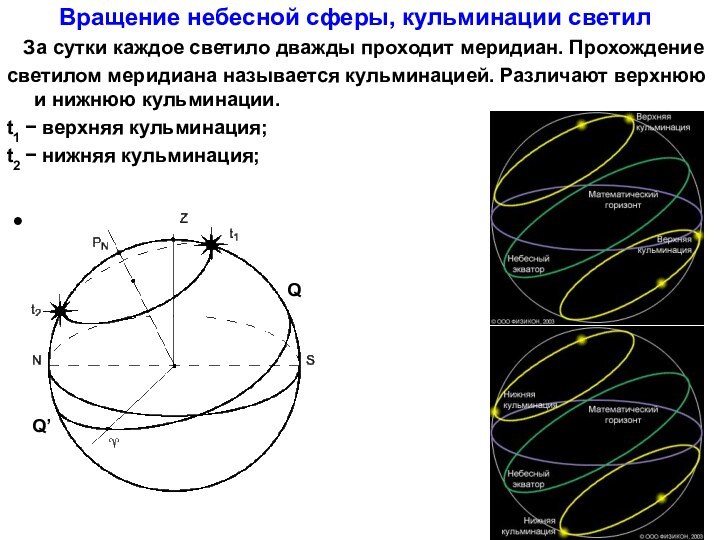
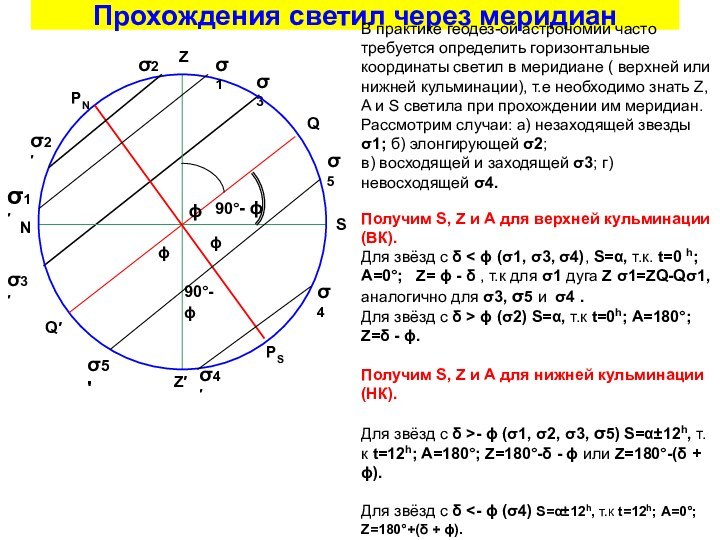
Плоскость, проходящая через отвесную линию и ось мира, пересекает небесную сферу по линии небесного меридиана. Небесный меридиан пересекается с истинным горизонтом в точках севера, N , и юга, S. А плоскости этих кругов пересекаются по полуденной линии. Небесный меридиан является проекцией на небесную сферу земного меридиана, на котором находится наблюдатель. Поэтому на небесной сфере есть только один меридиан, ведь наблюдатель не может находиться на двух меридианах одновременно!

на плоскость небесного меридиана

−
точка юга.

0°≤ Z≤ 180° 0° ≤ A

≤ 360°
-90°≤h ≤ 90°
Z+h= 90°

0° ≤ A ≤ 360°
-90°≤h ≤ 90°
Z+h= 90°
Горизонтальна система

координат

экватора, началь-
ная точка − верхняя точка
экватора.
Координаты:
склонение, дуга круга
Склонений

МО, обозначает-
ся δ .
Вторая координата – часо-
вой угол t .
Склонение выражается в
градусной мере, часовой угол
в часовой мере,

-90°≤δ≤ 90° ; 0h≤ t≤ 24h

начальная точка − точка весеннего равноденствия ♈
экватора.
Координаты:
склонение, дуга круга

Склонений МО, обозначает-
ся δ ,
вторая координата – прямое восхождение α.
Склонение выражается в
градусной мере, прямое восхождение
в часовой мере,

-90°≤δ≤ 90° ; 0h≤ α≤ 24h

t+α=s - звёздное время

является плоскость эклиптики. Северный полюс эклиптики обозначим через

ПN; по определению дуга PNПN    равна примерно 23,5°.   Южный полюс эклиптики обозначим как ПS, ПNПS − ось эклиптики.
Линия пересечения двух плоскостей - небесного экватора и эклиптики называется линией узлов. Эклиптика делит небесную сферу на два полушария: северное и южное.
Большой круг, проведенный через полюсы эклиптики и небесный объект, называется кругом широты.
Дуга круга широты AS , отсчитываемая от плоскости эклиптики, называется эклиптической широтой : AS=β .
Широта положительна в северном и отрицательна в южном полушарии    

Второй координатой является эклиптическая долгота λ, равная двугранному углу между большим кругом, который проходит через полюсы эклиптики и динамическую точку весеннего равноденствия, и кругом широты: ♈A=λ . Долгота измеряется от точки весеннего равноденствия от 0° до 360° против часовой стрелки, если смотреть с северного полюса эклиптики, то есть в направлении возрастания прямых восхождений.

каждое светило дважды проходит меридиан. Прохождение
светилом меридиана называется кульминацией.

Различают верхнюю и нижнюю кульминации.
t1 − верхняя кульминация;
t2 − нижняя кульминация;

Q

Q’

и заходящие звёзды


-(90°−ϕ) ≤ δ≤ (90°−ϕ)
3. Невосходящие звёзды
90°−ϕ
а
b

4. Звёзды, проходящие 1-ый
вертикал над горизонтом

0° ≤ δ≤ ϕ

5. Элонгирующие звёзды

δ > ϕ

О

90°−ϕ

90°−ϕ

90°−ϕ

Элонгирующие звёзды

кульминации
Если δ

δ
Если δ>ϕ (№2), то А=180°; S= α±12h; z=δ - ϕ

Для нижней кульминации
Если δ<ϕ (№1) , то А=180°; S= α±12h; Z=180°-(ϕ+δ)
Если δ>ϕ (№2), то А=180°; S= α±12h; Z=180°-(ϕ+δ)

ВК к северу от Z

ВК к югу от Z

требуется определить горизонтальные координаты светил в меридиане ( верхней

или нижней кульминации), т.е необходимо знать Z, A и S светила при прохождении им меридиан. Рассмотрим случаи: а) незаходящей звезды σ1; б) элонгирующей σ2;
в) восходящей и заходящей σ3; г) невосходящей σ4.

Получим S, Z и А для верхней кульминации (ВК).
Для звёзд с δ < ϕ (σ1, σ3, σ4), S=α, т.к. t=0 h; А=0°; Z= ϕ - δ , т.к для σ1 дуга Z σ1=ZQ-Qσ1, аналогично для σ3, σ5 и σ4 .
Для звёзд с δ > ϕ (σ2) S=α, т.к t=0h; А=180°; Z=δ - ϕ.

Получим S, Z и А для нижней кульминации (НК).

Для звёзд с δ >- ϕ (σ1, σ2, σ3, σ5) S=α±12h, т.к t=12h; А=180°; Z=180°-δ - ϕ или Z=180°-(δ + ϕ).

Для звёзд с δ <- ϕ (σ4) S=α±12h, т.к t=12h; А=0°; Z=180°+(δ + ϕ).

σ5'

σ5

- ϕ
t
180°− A
q

cosδ×sinϕ×cost
sinZ×sinA=cosδ×sint
sinδ= sinϕ×cosZ+ cosϕ×sinZ×cosAN

Производные формулы
ctgAN=sinϕ×ctg t - cosϕ×tgδ×cosect
cosA=(sinδ-sinϕ×cosZ)/(cosϕ×sinZ)

при Z = 90º, то по правилу Непера-Модюи:
cos z

= sinδ/sinϕ; cost= tgδ/tgϕ.

Sw = α + tw; SE = α + tE.
для δ > 0, φ > 0
tw = t, tE = 24 – t.

σ

q

имеем cos t = tg δ * tg φ;

cos A = −sinϕ/cosδ;

для φ > 0, δ > 0
t w = 12ʰ - t ; Aw = 180º - A;
tE = 12ʰ + 1; AE = 180º + A
для δ < 0
t w = t ; Aw = А;
tE = 24 – t; AE = 360º - A;
Sw = α + t w ; SE = α + tE;

σ

q

удаления от меридиана называются
Элонгациями. Различают западную Эw и

восточную ЭE элонгации. В элонгациях углы ZЭР равны 90°. Решая их по правилу Непера-Модюи получим:
cost=tgϕ / tgδ ; cosZ= sinϕ / sinδ ; sinA = cosδ / cosϕ .
Для западной элонгации: tw=t и AN=−A, а Sw =α +tW ; AW =180° +A .
Для восточной элонгации: tе=− t и AN=A, а SЕ =α +tЕ ; AЕ =180° + A .

Z

AE