- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему КУРС АСТОРОНИИ
Содержание
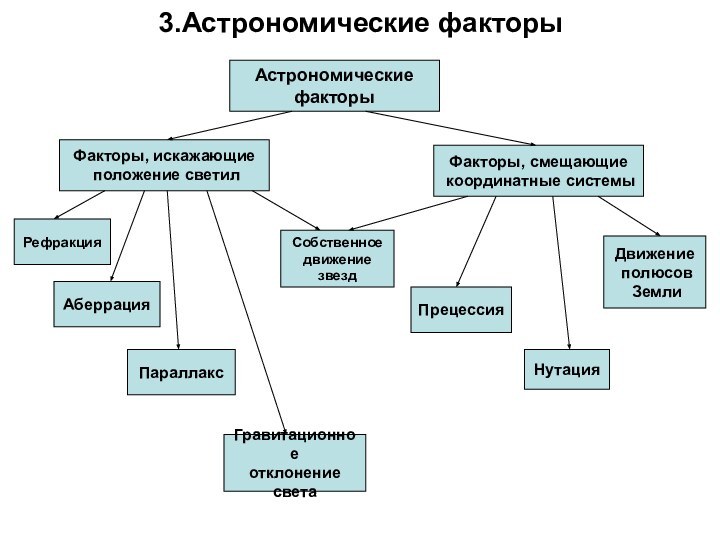
- 2. 3.Астрономические факторыАстрономические факторыФакторы, искажающие положение светил Факторы, смещающие координатные системыРефракцияАберрацияПараллаксСобственное движениезвездПрецессияНутацияДвижение полюсов ЗемлиГравитационное отклонение света
- 3. РЕФРАКЦИЯ , .
- 4. Если у нас есть абсолютные показатели
- 5. Вывод приближённой формулы рефракции Если представить атмосферу
- 6. где D – нормальная плотность воздуха при
- 7. Параллакср – параллактическое смещение светила(апекс)По теореме синусов
- 8. Суточный параллакс. Горизонтальный параллакс.sinp′=(R0 /d)sinz′
- 9. Годичный параллаксГодичный параллакс светила есть малый угол
- 10. Годичный параллаксdα-α0 = πcosδ?sin(α?-α0)secδ0 ; δ-δ0=π[sinδ?cosδ0-cosδ?sinδ0cos(α?-α0)]Учёт годичного
- 11. АберрацияАберрацией называют явление отклонения светового луча от
- 12. Аберрационное смещение светила на небесной
- 13. Смещение светил, вызванное годичной
- 14. Суточная аберрация Скорость вращения Земли
- 15. ПрецессияГреческий астроном Гиппарх (123 г. до н.э.)
- 16. Смещение полюса мира из-за лунно-солнечной прецессииПэ
- 17. Лунно-Солнечная прецессия и прецессия от планет. Прецессионные параметры.
- 18. Определение прецессионных параметровПоложение экваториальной системы относительно эклиптической
- 19. ПрецессияИзменение экваториальных координат вследствие прецессии можно представить
- 20. Нута́ция (от лат. nūtāre — колебаться) — слабое нерегулярное
- 21. Нутация, средний и истинный полюсРсПрецессия и полярная
- 22. Нутация в долготе и наклоне Нутационное движение разлагается
- 23. НутацияНутацию разделяют на долгопериодическуюΔψ ; Δε и
- 24. Собственное движение звездЗвезды движутся с разными скоростями и удалены от наблюдателя на различные расстояния. Вследствие этого взаимное расположение звезд меняется с течением времени. В течение одной человеческой жизни обнаружить изменения контура созвездия практически невозможно. Если проследить эти изменения в течение тысячелетий, то они становятся вполне заметными
- 25. Собственное движение звёздСобственное движение звезды также характеризуется двумя числами:µα – собственное движение по прямому восхождению, µδ –собственное движение по склонению, μ - полное собственное движение звезды выражается в секундах дуги в год и вычисляется по формуле: (3.16)
- 26. Движение географических полюсов. Мгновенная ось вращения Земли
- 27. Движение полюсаДвижение полюса на интервале 1900-2000 г.
- 28. Совместный учёт редукцийЕсли требуется преобразовать измеренные координаты
- 29. Приведение на видимое место В геодезической
- 30. Совместное влияние прецессии, нутации и собственного движения,
- 31. Видимые места звёзд в астрономическом ежегоднике (АЕ)В
- 32. Фундаментальные каталогиФундаментальный каталог (The Catalogue of Fundamental
- 33. Международная небесная система координатInternational Celestial Reference System
- 34. Скачать презентацию
- 35. Похожие презентации






![КУРС АСТОРОНИИ Годичный параллаксdα-α0 = πcosδ?sin(α?-α0)secδ0 ; δ-δ0=π[sinδ?cosδ0-cosδ?sinδ0cos(α?-α0)]Учёт годичного параллакса в экваториальных координатахгде α,](/img/tmb/12/1145385/53e98b198c411a42d51300101e5befe9-720x.jpg)






















Слайд 2
3.Астрономические факторы
Астрономические
факторы
Факторы, искажающие
положение светил
Факторы, смещающие
Слайд 4 Если у нас есть абсолютные показатели преломления
двух сред 1 и 2, то тогда
отсюда .
Если μ1,2 >1, то среда 2 плотнее среды 1, значит и ,
т.е при переходе из менее плотной среды в более плотную луч приближается к нормали.
Теперь рассмотрим с этих позиций прохождение луча света от светила через Земную атмосферу.
Земную атмосферу можно рассматривать как оптически прозрачную среду состоящую из слоев возрастающей плотности от верхней границы к поверхности Земли, а следовательно луч света проходя через нее будет преломляться.
Определение: Как само явление преломления в земной атмосфере лучей света, исходящих от
небесных светил, так и угол ρ, на который отклоняется луч в атмосфере, называется
астрономической рефракцией.
Реальная земная атмосфера по форме близка к сферической, вычисление рефракции при этом выполняется методом интегрирования (решение было пролучено Ньютоном), что является достаточно непростой задачей, поэтому точное значение рефракции получают из таблиц. Самые известные таблицы рефракции − Пулковские таблицы, но для многих случаев можно использовать приближённую формулу рефракции.
Слайд 5
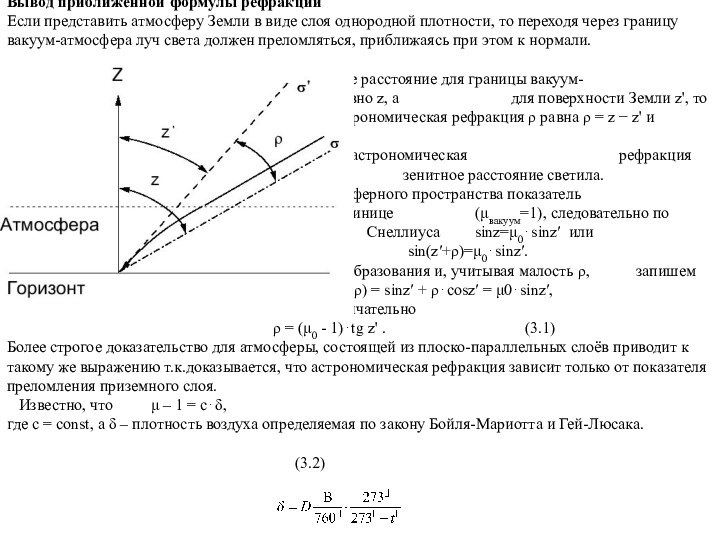
Вывод приближённой формулы рефракции
Если представить атмосферу Земли
в виде слоя однородной плотности, то переходя через границу
вакуум-атмосфера луч света должен преломляться, приближаясь при этом к нормали.Если зенитное расстояние для границы вакуум- атмосфера было равно z, а для поверхности Земли z', то астрономическая рефракция ρ равна ρ = z − z' и следовательно
z = z' + ρ, т.е астрономическая рефракция уменьшает зенитное расстояние светила.
Для внеатмосферного пространства показатель преломления равен единице (μвакуум=1), следовательно по закону Декарта- Снеллиуса sinz=μ0⋅sinz′ или
sin(z′+ρ)=μ0⋅sinz′.
После преобразования и, учитывая малость ρ, запишем sin(z′+ρ) = sinz′ + ρ⋅cosz′ = μ0⋅sinz′,
окончательно
ρ = (μ0 - 1)⋅tg z' . (3.1)
Более строгое доказательство для атмосферы, состоящей из плоско-параллельных слоёв приводит к такому же выражению т.к.доказывается, что астрономическая рефракция зависит только от показателя преломления приземного слоя.
Известно, что μ – 1 = с⋅δ,
где с = const, а δ – плотность воздуха определяемая по закону Бойля-Мариотта и Гей-Люсака.
(3.2)
Слайд 6 где D – нормальная плотность воздуха при В
= 760 мм.рт.ст. и 0° температуры по С (D
= 0,0012928);t° - температура. Подставим (2) в (1) получим
ρ = c·δ·tgz' = (3.3)
Величина С·D = 60″,3 получена из опыта (лучше определять из астрономических определений). Если не учитывать температуру и давление, то получим выражение для средней рефракции, которое используется для обработки приближенных определений
ρ = 60″,3 ·tgz'. (3.4)
Окончательно:
Выражение (3) называется приближенной формулой для рефракции, которая применяется для z≤60°÷70° (для z≤60° ошибка вычисления ρ ≤0.1″) более точные значения ρ получают учитывая сферичность слоев атмосферы и используя таблицы рефракции.
Слайд 7
Параллакс
р – параллактическое
смещение светила
(апекс)
По теореме синусов из
Δ-ка ОВΣ
sinp=(b/Δ)sinγ′ =(b/Δ)sinγ,
т.к. γ′≈γ
Или по малости
рp=206264.8″× (b/Δ)sinγ.
Законы параллактического смещения
1. Параллактическое смещение происходит по большому кругу;
2. Параллактическим смещением светило удаляется от апекса.
3. Синус параллактического смещения светила пропорционален синусу
углового расстояния светила от апекса перемещения наблюдателя.
Параллаксом называется изменение направления на объект при наблюдении его
из разных точек пространства
Слайд 8
Суточный параллакс.
Горизонтальный параллакс.
sinp′=(R0 /d)sinz′
sinp′=sinp0sinz′
или по малости р
p′=p0sinz
(3.5) z0=z- p0sinz (3.6)
где р′ − суточный параллакс в Т;
р0 − горизонтальный параллакс в Т
z′ - измеренное и исправленное за рефракцию z в Т; zc – геоцентрическое z .
Апекс для Т в надире, поэтому параллактическое смещение происходит в вертикале светила и азимут не изменяется.
Параллактическое смещение светила, возникающее вследствие суточного вращения
Земли вокруг оси или возникающее при наблюдении светила из различных пунктов
земной поверхности, называется суточным. Иначе можно сказать, что суточным
Параллаксом называется угол р′ под которым виден радиус Земли в месте наблюдения.
Если светило находится в горизонте, то суточный параллакс имеет максимальное
значение и называется горизонтальным параллаксом.
Слайд 9
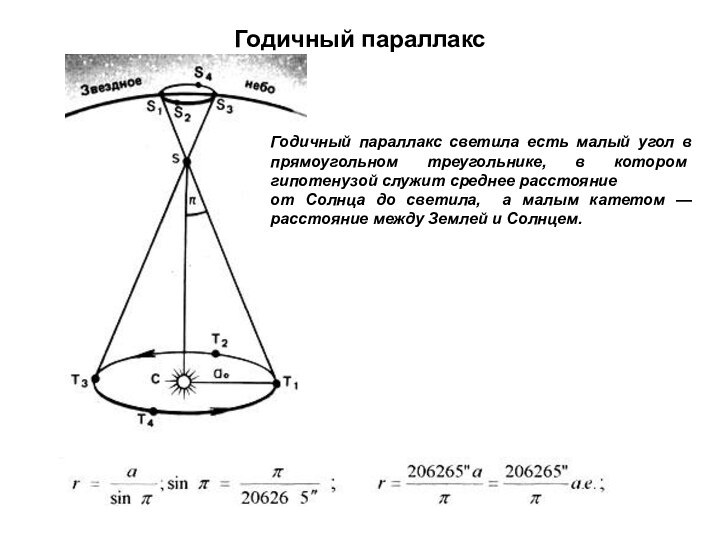
Годичный параллакс
Годичный параллакс светила есть малый угол в
прямоугольном треугольнике, в котором гипотенузой служит среднее расстояние
от
Солнца до светила, а малым катетом — расстояние между Землей и Солнцем.
Слайд 10
Годичный параллакс
d
α-α0 = πcosδ?sin(α?-α0)secδ0 ;
δ-δ0=π[sinδ?cosδ0-cosδ?sinδ0cos(α?-α0)]
Учёт годичного параллакса
в экваториальных координатах
где α, δ - геоцентрические координаты светила;
α0, δ0 – гелиоцентрические координаты светила
Где X и Y прямоугольные барицентрические координаты Земли на
данный момент
Учёт годичного параллакса в прямоугольных координатах
(3.7)
Слайд 11
Аберрация
Аберрацией называют явление отклонения светового луча от действительного
направления на светило, происходящее в результате сложения скорости света
с относительной скоростью движения пункта наблюдения.Наблюдения светил ведутся с движущейся Земли, следовательно должно наблюдаться влияние этого фактора на координаты звёзд.
Аберрация была объяснена Джеймсом Брадлеем в 1728г. С 1725 г. он проводил наблюдения ряда звезд, в частности γ Дракона. После учета необходимых поправок Брадлей обнаружил, что эта звезда, находящаяся в зените, совершает кажущееся движение по почти круговой траектории с диаметром ≈40.5″ . Для других звезд он наблюдал эллиптическое движение.
Аберрацию проще всего можно объяснить, проведя аналогию между распространением света и падением дождевых капель. При безветренной погоде капли падают вертикально, и человек не промокнет, если будет стоять неподвижно под зонтиком. Если же он побежит, то, чтобы не промокнуть, он должен наклонить зонт в сторону движения. Относительно движущегося человека дождевые капли уже не падают вертикально, а имеют горизонтальную составляющую скорости -V , если V - скорость человека относительно земли. Если c - вертикальная скорость движения капель, то угол β, на который нужно наклонить зонт, определяется уравнением tgβ=V/c.
по малости β можно записать:
β= 206264'', 8⋅sin γ , (3.8)
Где k= ⋅ 206264'', 8 − коэффициент аберрации
Слайд 12 Аберрационное смещение светила на небесной сфере
подчинено трем основным положениям:
1. Аберрационное смещение пропорционально синусу
углового расстояния между направлениями на светило и апекс движения наблюдателя.2. Аберрационное смещение светила на небесной сфере происходит по большому
кругу, проведенному через апекс движения наблюдателя и светило.
3. Аберрационным смещением светило приближается к апексу движения наблюдателя.
В соответствии с тремя видами движения Земли различают три вида аберрации: суточную аберрацию, годичную аберрацию и вековую аберрацию.
Вековая аберрация возникает вследствие движения всей Солнечной системы в пространстве. Скорость движения Солнечной системы и ее направление в течение очень длительного времени остаются постоянными. Поэтому изменение, которое это движение вносит в координаты звезд, не меняется по величине и его можно не учитывать. Вековую аберрацию, поскольку она не меняется для каждого светила, обнаружить непосредственно из наблюдений нельзя.
Годичная аберрация
Если подставит в выражение для k значения скорости Земли по орбите и скорости света, то коэффициент годичной аберрации будет равен 20",496. , а само значение будет:
β= 20",496 × sin γ.
При вычислении годичной аберрации принимается, что Земля движется вокруг Солнца по эллипсу и вектор ее скорости v лежит в плоскости эклиптики. Широта апекса равна 0°, а долгота LА меньше долготы Солнца L◉ примерно на 90°.
Слайд 13 Смещение светил, вызванное годичной аберрацией,
всегда направлено в сторону движения Земли, поэтому в течение
года видимое место (искаженное годичной аберрацией) описывает на небесной сфере около истинного места эллипс, большая полуось которого равна k и расположена параллельно эклиптике, а малая полуось равна k sin γ. Если звезда находится в полюсе эклиптики, то для нее эллипс превращается в круг с радиусом k; если же звезда находится на эклиптике, то для нее эллипс превращается в дугу. Влияние годичной аберрации на координаты светил можно записать:α'−α = −k (sinα sin L◉ + cos α cos L◉ cos ε) sec δ +k е (sinα sin Lp + cosα cos Lp cos ε) sec δ;
δ'−δ = − k sin L◉ cosα sinδ − k cosL◉ cos ε (tgε cos δ − sinα sinδ) − ke [sin Lp cosα sinδ +
+ cos Lp cosε (tg ε cos δ − sin α sin δ)].
В этих формулах k — постоянная годичной аберрации, принятое значение которой 20."496, Lp — долгота перигелия, L◉ — долгота Солнца, е — эксцентриситет орбиты Земли, координаты α и δ свободные от влияния годичной аберрации, а α' и δ'- видимые координаты светил. Введя обозначения
С = — k cos ε cos L◉ , D = —k sin L◉ , с = cos α sec δ, c' = tg ε cos δ — sin α sin δ , d = sin α sec δ d' = cos α sin δ
Запишем
α'−α = Сс +Dd ,
δ'−δ = Cc' + Dd'.
(3.9)
(3.10)
Слайд 14
Суточная аберрация
Скорость вращения Земли на
геоцентрической широте φ' равна:
V0 = 0,464 cos φ' км/сек,
поэтому выражение для суточной аберрации запишем:β" = 0",319 cos φ sin γ, где 0",319 – коэффициент суточной аберрации k0.
Суточная аберрация учитывается в горизонтальных координатах светил:
А = А' + k0 cos φ cosec z cos А,
z = z' + k0 cos φ cos z sin A.
Поправку за суточную аберрацию удобнее вводить в средние отсчёты времени
аберрацию
ΔТаб = −0,021scosZ .
Слайд 15
Прецессия
Греческий астроном Гиппарх (123 г. до н.э.) определяя
координаты звёзд и сравнивая их с аналогичными наблюдениями Аристилла
и Тимохариса, произведенными на 100 лет раньше нашел, что широты звезд остались неизмененными, а склонения заметно изменились. Это указывало на смещение экватора относительно эклиптики и следовательно смещение точки весеннего равноденствия (ТВР, ♈) навстречу движения Солнца по эклиптике. Явление это на латыни получило название прецессия, что можно перевести как предварение равноденствия.Сущность этого явления объяснил Ньютон. Причиной прецессии являются следующие факторы:
гравитационное влиянии Солнца, Луны и планет;
- полярное сжатие Земли и неравномерное распределение масс в её теле;
- наклон оси вращения Земли к плоскости её орбиты.
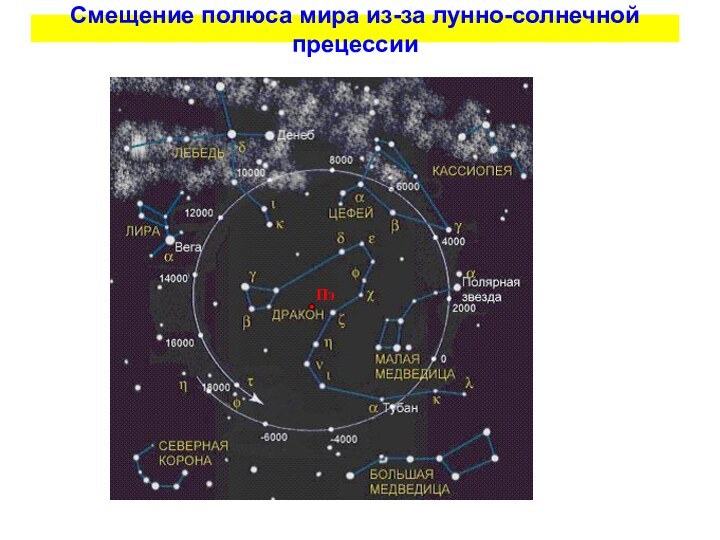
Полярное сжатие и наклон оси вращения приводит к тому, что экваториальные избытки притягиваются Луной и Солнцем с разной силой, что вызывает появления момента стремящегося изменить наклон оси вращения, а это ведёт к возникновению вращательного момента. В результате ось вращения Земли описывает окружность вокруг оси эклиптики с периодом примерно 25700 лет. Это явление называется лунно-солнечной прецессией и в результате ТВР смещается по эклиптике за год на 50,″39 . Влияние планет приводит к вращению плоскости эклиптики вокруг оси, лежащей в плоскости эклиптики с эклиптической долготой λ=174.°85. В результате ТВР смещается за год на 0,″10 вдоль эклиптики в направлении движения Солнца, а наклон эклиптики к экватору уменьшается за год на 0,″47.
Слайд 18
Определение прецессионных параметров
Положение экваториальной системы относительно эклиптической системы
может быть задано тремя углами Эйлера:
Угол
равен дуге эклиптики и называется лунно-солнечной прецессией за промежуток времени . В результате лунно-солнечной прецессии средняя мгновенная точка весеннего равноденствия смещается на запад по эклиптике из-за прецессионного движения экватора. Угол равен дуге среднего мгновенного экватора (А) и называется прецессией от планет. В результате прецессии от планет средняя мгновенная точка весеннего равноденствия смещается вдоль среднего мгновенного экватора.
Наклон мгновенной эклиптики Е к экватору А равен а эклиптики Ео на начальную эпоху к экватору А′ равен .
Слайд 19
Прецессия
Изменение экваториальных координат вследствие прецессии можно представить в
виде рядов Тейлора:
.
Для геодезической астрономии и промежутков времени в
десятки лет достаточно разложения до 3-го порядка, а для промежутка меньше года можно ограничиться первой производной.Значения годичной прецессии для светил Поправки в экваториальные координаты за годичную прецессию
dα/dt=m+n×sinα×tgδ ; Δα= (m+n×sinα×tgδ)×(T-Т0)/15; dδ/dt=n×cosα . Δδ= (n×cosα) × (T-T0)
Лунно-солнечная прецессия
Прецессия от планет
(прецессия по прямому восхождению)
(прецессия по склонению)
(значения для эпохи 2000.0)
Из прямоугольного треугольника ♈♈0N получим:
(3.11)
(3.12)
(3.13)
(3.14)
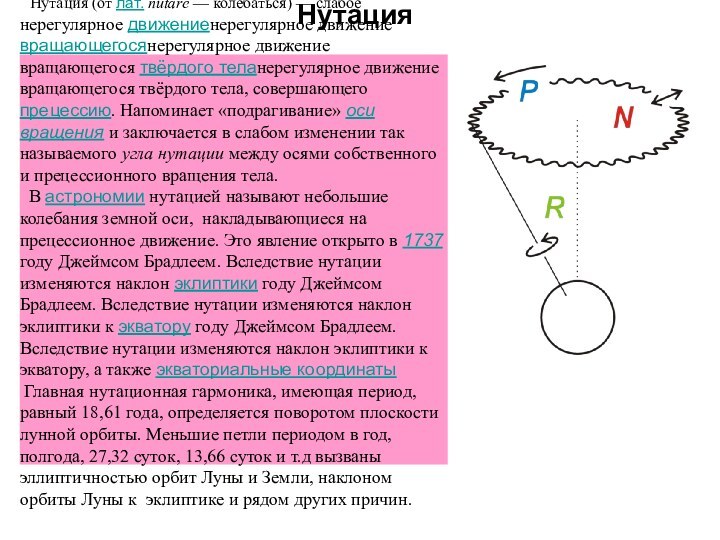
Слайд 20 Нута́ция (от лат. nūtāre — колебаться) — слабое нерегулярное движениенерегулярное
движение вращающегосянерегулярное движение вращающегося твёрдого теланерегулярное движение вращающегося твёрдого
тела, совершающего прецессию. Напоминает «подрагивание» оси вращения и заключается в слабом изменении так называемого угла нутации между осями собственного и прецессионного вращения тела.В астрономии нутацией называют небольшие колебания земной оси, накладывающиеся на прецессионное движение. Это явление открыто в 1737 году Джеймсом Брадлеем. Вследствие нутации изменяются наклон эклиптики году Джеймсом Брадлеем. Вследствие нутации изменяются наклон эклиптики к экватору году Джеймсом Брадлеем. Вследствие нутации изменяются наклон эклиптики к экватору, а также экваториальные координаты
Главная нутационная гармоника, имеющая период, равный 18,61 года, определяется поворотом плоскости лунной орбиты. Меньшие петли периодом в год, полгода, 27,32 суток, 13,66 суток и т.д вызваны эллиптичностью орбит Луны и Земли, наклоном орбиты Луны к эклиптике и рядом других причин.
Нутация
Слайд 21
Нутация, средний и истинный полюс
Рс
Прецессия и полярная нутация Экваториальная
нутация
Полюс мира, двигающийся только в результате прецессии называется средним
полюсом Рс , положение полюса с учётом влияния нутации называется истинным полюсом Р. Этим полюсам соответствуют средний экватор и истинный экватор.Главное нутационное движение полюса мира можно представить в виде эллипса с полуосями, равными в дуговой мере 9,2″ и 6,9″.
Слайд 22
Нутация в долготе и наклоне
Нутационное движение разлагается на
две главные компоненты:
Δψ=-17.2″×sinΩ − нутацию в долготе и
Δε=9.2″×cosΩ − нутацию в наклоне, где Δψ - нутация по долготе; Δε - нутация в наклоне; Ω - долгота восходящего узла лунной орбиты.
Теория нутации Земли МАС1980 включает 106 гармоник нутационного движения;новая теория нутации МАС2000 почти 1500 гармоник с периодами от 2 суток до 18,6 лет.
Слайд 23
Нутация
Нутацию разделяют на долгопериодическую
Δψ ; Δε и короткопериодическую
dψ; dε .
Суммарное влияние обозначается:
[Δψ]= Δψ+ dψ и
[Δε]= Δε+ dε .Влияние нутации на экваториальные
координаты можно записать:
α-α0=[ Δψ](cosε+sinεsinα0tgδ0)-[Δε]cosα0tgδ0
δ-δ0 =[Δψ]sinεcosα0+[Δε]sinα0
Совместный точный учёт прецессии и
нутации в экваториальных координатах
от среднего равноденствия rcp к истинному
rист производится по формуле rист =NPrcp ,
где N – матрица нутации, P − матрица
прецессии.
(3.15)
Слайд 24
Собственное движение звезд
Звезды движутся с разными скоростями и удалены от наблюдателя на различные
расстояния. Вследствие этого взаимное расположение звезд меняется с течением
времени. В течение одной
человеческой жизни обнаружить изменения контура
созвездия практически невозможно. Если проследить эти изменения в течение
тысячелетий, то они становятся вполне заметными
Слайд 25
Собственное движение звёзд
Собственное движение звезды также характеризуется двумя числами:
µα – собственное движение по прямому восхождению,
µδ –собственное движение по склонению,
μ - полное собственное движение звезды
выражается в секундах дуги в год
и вычисляется по формуле:
(3.16)
Слайд 26 Движение географических полюсов. Мгновенная ось вращения Земли не
сохраняет в теле Земли неизменного направления, вследствие чего происходит
перемещение географических Полюсов по земной поверхности; это явление называется движением полюсов Земли. Сведения о движении полюсов имеют важное значение в астрономии и геодезии, т.к. оно вызывает непрерывные изменения координат точек поверхности Земли и азимутов земных предметов, что сказывается на результатах астрономических и геодезических измерений. Для получения этих сведений в 1899 была создана Международная служба широты, переименованная в 1961 в Международную службу движения полюсов Земли (см. Служба движения полюса международная). В её состав входят 5 станций, ведущих наблюдения изменений широт, и Центральное бюро, которое на основе этих наблюдений вычисляет координаты Полюсы географические Станции расположены на одной географической параллели 39° 8’ с. ш. и снабжены однотипными инструментами. В число их входят станции: Мидзусава (Япония), Китаб (СССР), Карлофорте (Италия), Гейтерсберг (США), Юкайа (США). В СССР наблюдения для службы движения полюсов Земли ведутся также в Пулкове, Москве, Полтаве, Казани, Горьком, Иркутске, Благовещенске. Движение полюсов Земли изучается относительно т. н. условного международного начала координат Сев. полюса Земли (ему соответствует «условный» экватор), положение которого установлено решением 13-й Генеральной ассамблеи Международного астрономического союза в 1967. В этой точке проводится плоскость К, касательная к поверхности земного сфероида. По результатам астрономических наблюдений широты j на станциях определяется плоскость мгновенного экватора Земли. Перпендикуляр СР к этой плоскости практически совпадает с мгновенной осью вращения Земли, а точка Р, в которой он пересекает плоскость К, — с мгновенным полюсом Земли. В плоскости К вводят координатную систему: ось ОХ проводят в направлении меридиана Гринвича, OOY — под углом 90° к З. от него. Координаты точки Р в этой системе называется координатами мгновенного полюса Земли. Они связаны с широтой пункта наблюдений формулой, предложенной в 1893 С. К. Костинским: х cos l + у sin l = j — j0, где l — долгота пункта наблюдения. Данные о движении Полюсы географические показывают, что полюс Р движется по поверхности Земли в направлении её суточного вращения вокруг полюса инерции I, в которой наименьшая ось эллипсоида инерции Земли пересекает плоскость К и при этом описывает неправильную спиралевидную кривую — полодию, витки которой постепенно смещаются относительно условного международного начала О в сторону Гренландии. Полодия Южного полюса имеет такую же форму, как и Северного.
Слайд 27
Движение полюса
Движение полюса на интервале 1900-2000 г. (вековой
ход - жирная линия) и на интервале 1995-2000 г.
Отсчет координат ведется от Условного Международного Начала (МУН) или (CIO). Координаты мгновенного полюса x и y вычисляются международным бюро времени (МБВ), а также национальными службами временина основании спутниковых измерений, лазерной локации Луны, РСДБ-измерений и публикуются в специальных бюллетенях.
Поправки за приведение мгновенных координат и азимутов к среднему полюсу вычисляют по формулам:
Δϕ=y×sinλ - x×cosλ ;
Δλ=-(x×sinλ + y×cosλ)tgϕ/15 ;
Δa= -(x×sinλ + y×cosλ)secϕ,
а исправленные значения координат и азимута равны:
ϕМУН=ϕнабл+ Δϕр;
λ МУН= λ набл+ Δ λр ;
а МУН= а набл+ Δ ар
(3.17)
(3.18)
Слайд 28
Совместный учёт редукций
Если требуется преобразовать измеренные координаты звезды
или планеты к экватору и равноденствию стандартной эпохи, то
классический метод обработки оптических астрометрических наблюдений заключается в следующем.Из наблюденных зенитных расстояний вычитаются поправки за рефракцию и находятся прямые восхождения и склонения небесных тел для точки на поверхности Земли, лишенной атмосферы.
Учитывая поправки, связанные с суточной аберрацией, находятся координаты, которые отнесены к невращающейся Земле (видимые координаты).
Учет суточного параллакса приводит к переносу начала отсчета в центр Земли.
Учет годичной аберрации (для близких небесных тел - планетной аберрации) приводит к переносу начала системы отсчета в барицентр солнечной системы. В результате выполненной редукции координаты небесных тел определяются относительно истинного экватора и равноденствия даты в барицентрической системе отсчета (истинные координаты) .
Учет нутации позволяет определить координаты, отнесенные к среднему экватору и равноденствию даты.
Исправляя координаты за прецессию и собственное движение, получим координаты небесных тел, отнесенные к среднему экватору и равноденствию стандартной эпохи (эпохи каталога звёздных положений). Положение небесных тел в этой системе координат является средним стандартным местом
Слайд 29
Приведение на видимое место
В геодезической астрономии
при обработке астрономических определений используют
видимые геоцентрические экваториальные координаты
светил. Наблюдённое на пункте направление на светило приводится к видимому, отнесённому к центру Земли путём введения поправок за рефракцию, сточную аберрацию и суточный параллакс (последняя поправка только для тел солнечной системы).Переход от средних координат эпохи каталога t0 к видимым координатам момента наблюдения выполнятся в два этапа. На первом этапе учитывая влияние прецессии и собственных движений переходят к средним координатам года наблюдения (средину года, эпоха наблюдения t ). Такой переход выполняется по формулам:
На втором этапе переходят от средних координат эпохи наблюдения t к видимым координатам момента наблюдения. Этот промежуток не превышает половины года и обозначается через τ. Первоначально также учитываем влияние прецессии и собственных движений светил:
; ,
где τ выражается в долях года от средины года t.
Далее, учитывая нутацию по формулам (3.15), перейдём к истинным координатам на момент наблюдения.
(3.19)
(3.20)
Слайд 30 Совместное влияние прецессии, нутации и собственного движения, сохраняя
за суммами долгопериодических членов обозначения Δψ и Δε и,
обозначая суммы короткопериодических членов через dψ и dε , приводит к формулам:После ряда преобразований, введя обозначения, которые называются большие и малые бесселевы буквы:
запишем окончательно:
где Cc, Dd, Cc′, Dd′ - учитывают влияние годичной аберрации (3.10).
(3.21)
Слайд 31
Видимые места звёзд в астрономическом ежегоднике (АЕ)
В АЕ
для 779 ярких звёзд приведены видимые места для верхней
кульминации в Гриниче . Из них для 47 близполюсных (δ>80°) на каждые сутки года и для 732 (δ<80°) через 10 суток.Для промежуточных моментов видимые места находят с помощью линейной интерполяции.
Слайд 32
Фундаментальные каталоги
Фундаментальный каталог (The Catalogue of Fundamental Stars) —
серия из шести звёздных каталогов, созданных в разное время
для фиксации на небе стандартной системы координатфиксации на небе стандартной системы координат — Международной небесной системы координат.
FK4 — каталог, опубликованный в 1963 году и содержащий данные о 1535 звёздах.
FK4S — дополнение к каталогу FK4.
FK5 опубликован в 1988 году и содержит обновлённые данные о 1535 зведах. и на тот момент являлся оптической реализацией Международной небесной системы координат. Все вышеназванные каталоги содержат данные, полученные только из наземных наблюдений.
FK6 — последний Фундаментальный каталог, является комбинацией результатов наземных наблюдений и космического астрометрического проекта Hipparcos. Каталог состоит из трёх частей. Первая часть содержит 878 так называемых фундаментальных звёзд, то есть звёзд, которые с большой вероятностью не являюся двойными, то есть звёзд, которые с большой вероятностью не являюся двойными. Двойственность звезды вносит неопределённость в собственное движение, что снижает точность астрометрических измерений. Средняя ошибка собственных движений почти в два раза меньше, чем у Hipparcos и составляет 0,35 mas/год. Третья часть содержит 3272 звезды. Введён резолюцией МАС , принятой в 1997 году. В АЕ положения и собственные движения звёзд на его основе публикуются с 2004 года. FK6 – оптическая реализация системы ICRS.
Слайд 33
Международная небесная система координат
International Celestial Reference System (ICRS,
Международная небесная система координат или Международная система астрономических координат)
— на данный момент стандартная небесная система координат) — на данный момент стандартная небесная система координат, принятая на 23-м съезде МАС) — на данный момент стандартная небесная система координат, принятая на 23-м съезде МАС в 1997) — на данный момент стандартная небесная система координат, принятая на 23-м съезде МАС в 1997 году. Началом отсчета является барицентр) — на данный момент стандартная небесная система координат, принятая на 23-м съезде МАС в 1997 году. Началом отсчета является барицентр Солнечной системы. Система основана на кинематическом принципе, то есть оси жёстко зафиксированы в пространстве относительно самых удаленных объектов наблюдаемой вселенной. ICRS — набор договоренностей и основополагающих принципов построения небесной системы координат.International Celestial Reference Frame (ICRF, Международный набор реперов системы астрономических координат) — реализация небесной системы координат ICRS. По своей сути это каталог, содержащий координаты опорных бесконечно удаленных объектов. В каталог входят 212 внегалактических радиоисточников (квазаров), координаты которых измерены с точностью до 1 mas (миллисекунды дуги) с помощью РСДБ наблюдений. В каталог также включены дополнительно 396 объектов, координаты которых измерены с меньшей точностью. Оптической реализацией является принятый фундаментальный каталог , сейчас это FK6.





























