Презентация на тему Позиционная астрономия и небесная механика в 18 веке

веке
Поиск годичного параллакса
Гринвичская обсерватория
1725 г. – Джеймс Брадлей (профессор

в Оксфорде) - проверка результата Гука
(якобы годичный параллакс γ Draconis – 30 “)
Зенитный сектор радиусом 7.2 м, установленный в меридиане. Год наблюдений
Начинал наблюдения Самуэль Молинё (1689-1728), позже, назначенный в Адмиралтейство

веке
Поиск годичного параллакса
Гринвичская обсерватория
Декабрь-март – 20” на юг
Март-сентябрь -

40” на север
К началу декабря – в прежнее положение
Погрешность наблюдений - <2”
При параллактическом смещении – наибольшее смещение – на три месяца раньше! (Зимой – как можно дальше к югу, летом – как можно дальше к северу)

веке
Поиск годичного параллакса
Гринвичская обсерватория
Другие звезды: изменения тем меньше, чем

ближе к эклиптике звезды
(Берри, стр.223)
1728 г. – объяснение – движение Земли! (Начало 1728 г. – доклад Королевскому Обществу)
Аберрация (не нутация) – первое доказательство движения Земли!
(Климишин, стр.223)

веке
Поиск годичного параллакса
Гринвичская обсерватория
Тогда же сделан вывод – на

имеющихся инструментах параллактическое смещение необнаружимо
Первый параллакс – 1822 г. (сто лет спустя!) – В.Я.Струве (1793-1864) – α Орла – Альтаир (0.181”)

веке
Нутация
Гринвичская обсерватория
1742 г. – Брадлей – королевский астроном
У звезды

γ Draconis были обнаружены вторичные колебания положений с периодом примерно 19 лет и амплитудой 18”. Нутация
Объяснение дано другими (1748 г.) – колебания оси вращения Земли, вызванные тяготением Луны и обусловленные несферичностью Земли
(Предел точности наблюдений. Редукции. После смерти Брадлея его наблюдения обработал Бессель)

веке
Фигура Земли
Жан Рише. 1672 г. - экспедиция в Кайенну

(φ = +5о)
Маятник качается медленнее
g – меньше; действие центробежных сил + сплюснутость Земли (Гюйгенс – 1683 г., Ньютон)
Гюйгенс (1687) – сплюснутость 1 / 572
Ньютон – 1 / 230 (1 / 298.3) – объяснил прецессию, предсказал нутацию

веке
Фигура Земли
Тем не менее французские астрономы (многолетние наблюдения дуги

меридиана) сделали вывод об уменьшении дуги в 1о к северу
(Климишин, стр.191, слова Вольтера)
Граф Морепа добился в 1734 г. финансирования экспедиции

веке
Фигура Земли
Парижская обсерватория
(16 мая) 1735 г. – руководитель –

академик Луи Годен. Луи Бугер (гидрограф), Шарль-Мари Ла Кондамин (военный математик и астроном), Жозеф Жюссьё (врач-натуралист).
Экспедиция в северную часть Перу (ныне Эквадор, горная долина Кито) – Анды, дуга меридиана в 3o - 320 км, от от местечка Яруки, близ Кито, до точки за городом Куэнкой.
(Предполагалось измерить и дугу в направлении запад-восток)
Завершение экспедиции – 1743 г.

веке
Фигура Земли
Парижская обсерватория
(Годен остался в Перу и стал преподавателем

Университета в Лиме. Академия наук исключила его из своего состава (растраты). Позже он перебрался в Бразилию, затем в Испанию.
Ла Кондамин занимался переправкой драгоценностей.
Буге самостоятельно добрался до Парижа 27 июня 1744 г.
Ла Кондамин пересек континент по течению Амазонки (каучук), а потом направился к французскому порту в Кайенне. 30 ноября 1744 г. он высадился в Амстердаме.)

веке
Фигура Земли
Парижская обсерватория
(2 мая) 1736 г. – Мопертюи и

Клеро – экспедиция в Лапландию, Торнио – дуга меридиана в 57’
Завершение экспедиции – 1738 г.

веке
Фигура Земли
Парижская обсерватория
Кито - 1 град. = 56 753

туаза
(“французский” градус = 57 057 туазов)
Торнио - 1 град. = 57 438 туазов
К 1740 г. вопрос был решен: с увеличением широты длина 1о дуги меридиана возрастает!
Торнио-Париж – сжатие 1/114
Кито-Париж – 1/279

веке
Масса Земли и масса Солнца
(Ньютон сделал относительные измерения)
Третий закон

Кеплера (сначала для системы Земля-Луна, а потом – Солнце-Земля)

веке
Масса Земли и масса Солнца

Ньютон – в 5 раз

тяжелее воды. Оценка без измерений
(Климишин, стр. 194)
1749 г. наблюдения в Перу вблизи горы Чимборасо (Пьер Бугер и Шарль Мари Ла Кондамин). Отвес отклоняется на 7-8”

веке
Масса Земли и масса Солнца
1774 г. - Невилл Маскелайн

(1732-1811) выполнил аналогичные измерения на севере Шотландии (вблизи горы Шегальен, или Шихаллион, над озером Тэй). (Линии равных высот)
Измерения зенитного расстояния полюса на одном меридиане к северу и к югу от хребта
Расстояние 1330 м. Разность зенитных расстояний – 43“. Измерения - 54.8” (отклонение отвеса - 5.9”)

веке
Масса Земли и масса Солнца
1774 г. - Невилл Маскелайн

- измерения вблизи горы Шихаллион
Плотность Земли – в 1.8 раза превышает плотность горы. При средней плотности гранита 2.6 г/см3 –

веке
Масса Земли и масса Солнца
1797 г. - Генри Кавендиш

(1731-1810) “заменил” гору двумя свинцовыми шарами по 158 кг каждый. Масса пробных тел по 729 г. Подвешены на горизонтальной деревянной палочке, закрепленной в центре масс серебряной нитью. Измерялся угол закрутки нити


Масса Земли - 5.98*1027 г
Масса Солнца – 2*1033 г – взвешено при помощи деревянной палочки!

веке
Определение параллакса Солнца
Античное значение (пользовался еще Тихо Браге) параллакса

Солнца 3’
Кеплер по наблюдениям Марса (Тихо) вывел, что параллакс Солнца < 1’
Около 1630 г. Венделин (методом Аристарха, но уже пользуясь телескопом) для треугольника Аристарха определил угол Земля-Луна-Солнце в первую четверть:
90o – 0’.25 (!)

веке
Определение параллакса Солнца
Жан Рише. Осень 1672 г. - экспедиция

в Кайенну (φ = +5о). Марс в противостоянии. Расстояние Земля-Марс 0.37 а.е.
Кассини в Париже: параллакс Марса < 25”, следовательно параллакс Солнца <10” (9”.5)
Расстояние до Солнца – 140 000 000 км (!)

веке
Определение параллакса Солнца
Николай Луи де Лакайл
1750 г. –

экспедиция на мыс Доброй Надежды (5 лет) Параллакс Луны (57’5”)
Наблюдения Марса в противостоянии и серпа Венеры вблизи нижнего соединения. Европейские корреспондирующие результаты не очень точные
По наблюдениям Марса – 10”.2
По наблюдениям Венеры – 10”.6

веке
Определение параллакса Солнца
1676-1678 гг. – о. св.Елены – попытка

определить параллакс Солнца, наблюдая прохождение Меркурия по диску Солнца (1677). Неудачная (45” вместо 8.79“)
Эдмунд Галлей предложил в 1691 г. использовать для решения этой задачи прохождение Венеры – в 1761 г. и в 1769 г.
1716 г. – еще один призыв

веке
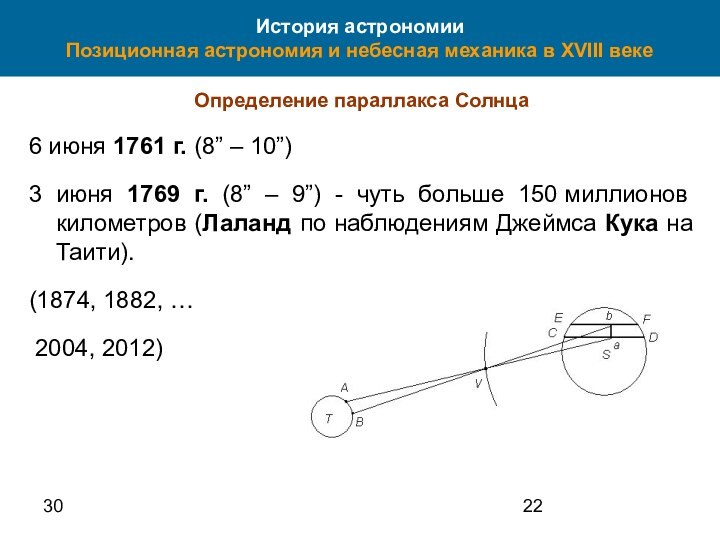
Определение параллакса Солнца
6 июня 1761 г. (8” – 10”)

3 июня 1769 г. (8” – 9”) - чуть больше 150 миллионов километров (Лаланд по наблюдениям Джеймса Кука на Таити).
(1874, 1882, …
2004, 2012)

веке
Проблема устойчивости Солнечной системы
1625 г. – Кеплер – Юпитер

и Сатурн уклоняются от движения по своим орбитам
Галлей – Юпитер движется ускоренно, а Сатурн замедленно. (За 1000 лет уклонения на 0o57’ и 2o19’ соответственно)
Возрастание скорости движения Луны

веке
Теория движения Луны
Проблема долгот
Погрешность в 1’ – погрешность координат

до 27 морских миль (до 50 км)
Галлей – 18 лет наблюдений

веке
Теория движения Луны
Д’Аламбер, Клеро, Эйлер
Д’Аламбер, Клеро и Эйлер -

задача трех тел в форме, пригодной для лунной теории
Жан Д’Аламбер (1717-1783) – “Аналитическая механика” (1743) – общий подход к составлению дифференциальных уравнений движения
Неравенства Луны. Точная теория прецессии и физический смысл явления нутации (1749)

веке
Теория движения Луны
Д’Аламбер, Клеро, Эйлер
Алексис Клод Клеро (1713-1765) –

премия Петербургской академии (1752 г.) – “Теория Луны”. (Комета Галлея)
До этого (1746 г.) – теория давала скорость вращения большой оси лунной орбиты 20o, а наблюдения в два раза больше
Попытка “уточнить” закон всемирного тяготения
F = Gm1m2 / r2 *(1 + α / rn)

веке
Теория движения Луны
Возмущенное движение
Леонард Эйлер (1707-1783) – 1753 г.

– “Теория движений Луны” – премия Парижской академии 1752 г.
Эйлер – “Новая теория движения Луны” (1755). Бесконечные ряды для представления оскулирующих элементов. Вековые и периодические члены
Товия Майер (1723-1762) – объединение теории и практики (теория Эйлера, но амплитуда отклонений из наблюдений). Ошибки до 1’.5

веке
Проблема устойчивости Солнечной системы
Возмущенное движение
Вековые и периодические члены (впоследствие

– благодаря оценке отклонений элементов орбит удалось открыть Нептун и Плутон)
Эйлер: в параметрах орбит Юпитера и Сатурна есть вековые члены
1763 г. – Жозеф Лагранж (1730-1813) – подтвердил присутствие вековых членов
1773 г. Иоганн Генрих Ламберт – замедление Юпитера и ускорение Сатурна – периодические члены!

веке
Проблема устойчивости Солнечной системы
Симон Лаплас (1749-1827)
1773 г. – учел

большее число членов. Система Солнце-Юпитер-Сатурн – устойчива
Большие полуоси – периодические изменения
1776 г. – Лагранж – эксцентриситет и наклон – периодические изменения
1784 г. – Лаплас: