Слайд 2
Классификация нормальных звезд
Спектры большинства звезд эмпирически удалось расположить

в виде последовательности, вдоль которой линии одних химических элементов
постепенно ослабевают, а других – усиливаются. Сходные между собой спектры объединяются в спектральные классы. Тонкие различия между ними позволяют выделить подклассы. Дальнейшие исследования показали, что звезды, принадлежащие различным спектральным классам, отличаются своими температурами.
В Гарвардской классификации спектральные типы (классы) обозначены буквами латинского алфавита: О, В, A, F, G, К и М. Поскольку в эпоху разработки этой классификации связь между видом спектра и температурой не была еще известна, то после установления соответствующей зависимости пришлось изменить порядок спектральных классов, который первоначально совпадал с алфавитным расположением букв (мнемоническое правило: O Be A Fine Girl Kiss Me).
Внутри каждого спектрального класса можно установить плавную последовательность подклассов, переходящих из одного в другой. Каждый класс (кроме класса О) делится на 10 подклассов, обозначаемых цифрами от 0 до 9, которые ставятся после обозначения спектрального класса, например, В8, А0, G5. Спектральный класс О подразделяется на подклассы от O2 до O9,5.
Слайд 5
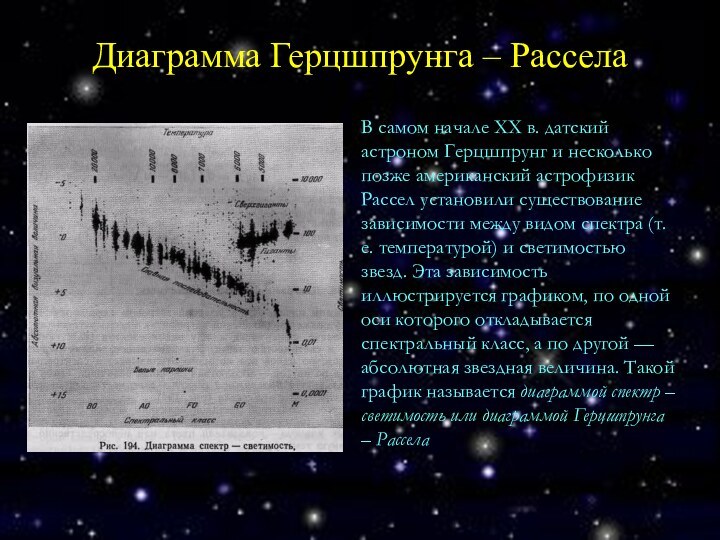
Диаграмма Герцшпрунга – Рассела
В самом начале XX в.
датский астроном Герцшпрунг и несколько позже американский астрофизик Рассел
установили существование зависимости между видом спектра (т.е. температурой) и светимостью звезд. Эта зависимость иллюстрируется графиком, по одной оси которого откладывается спектральный класс, а по другой — абсолютная звездная величина. Такой график называется диаграммой спектр – светимость или диаграммой Герцшпрунга – Рассела
Слайд 8
Классы светимости
Внимательное изучение диаграммы позволяет выделить на ней
ряд других последовательностей, правда, обладающих значительно большей дисперсией, чем
главная. Эти последовательности называются классами светимости и обозначаются римскими цифрами от I до VII, проставленными после наименования спектрального класса. Таким образом, полная классификация звезд оказывается зависящей от двух параметров, один из которых характеризует спектр (температуру), а другой – светимость. Солнце, относящееся к главной последовательности, попадает в V класс светимости и обозначение его спектра G2V. Эта классификация звезд называется МКК (Моргана, Кинана, Кельман).
Слайд 9
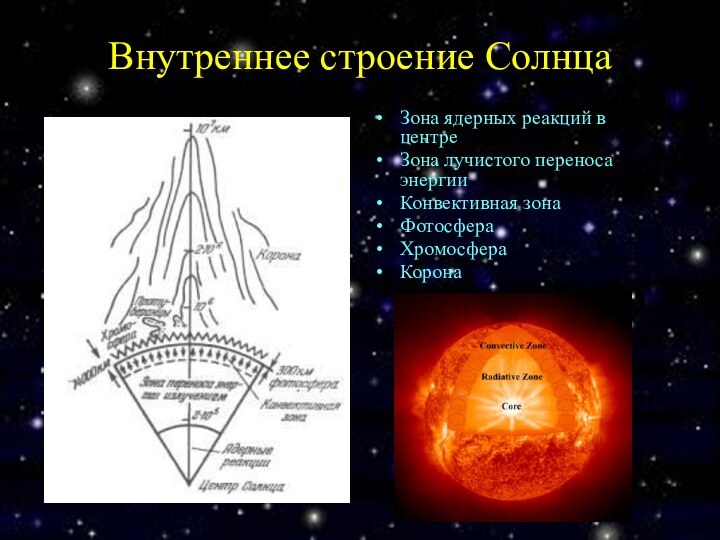
Внутреннее строение Солнца
Зона ядерных реакций в центре
Зона лучистого
переноса энергии
Конвективная зона
Фотосфера
Хромосфера
Корона
Слайд 13
Физические основы внутреннего строения звезд
Нет ничего проще, чем
звезда.
(А. Эддингтон)
Физическое состояние стационарных звезд определяется условиями гидростатического (макроскопические
параметры - масса, радиус - изменяются на больших временах >> динамического времени) и теплового (звезды не взрываются, их светимость меняется плавно) равновесия.
Слайд 14
Гидростатическое равновесие
Для сферически -симметричного случая
Прямым следствием уравнения
гидростатического равновесия является теорема вириала, связывающая тепловую (кинетическую) и
потенциальную (гравитационную) энергию стационарной звезды. Умножая обе части уравнения гидростатического равновесия на r и интегрируя по dm по частям, получим
Слайд 15
Политропная модель
Удельная тепловая энергия
(γ – показатель, n –
индекс политропы)
Отсюда можно, например, оценить температуру в центре Солнца.
Пусть вся звезда состоит из идеального одноатомного газа, γ =5/3, Q = (3/2)NkT. С учетом молекулярного веса получим T ~ 107 K. Точное значение – 14·106 K.
(адиабата) На единицу массы
Слайд 16
Частные случаи политропных моделей
n = 3/2, γ =
5/3 (идеальный одноатомный газ)
U = -2Q, E = -Q
Звезда
обладает отрицательной теплоемкостью,
dE/dT < 0 – устойчивое тепловое равновесие.
n = 3, γ = 4/3 (реализуется в белых карликах и в больших горячих звездах)
U = -Q, E = 0
Равновесие возможно только при одном определенном значении массы,
M ~ (K/G)3/2
Радиус звезды может быть любым.
Слайд 17
Теория белых карликов
Плотность очень велика, ρ ~ 105–109
г/см3. Вещество состоит из ядер и свободных электронов, которые
подчиняются статистике Ферми – Дирака.
Объем фазовой ячейки
Число электронов в единице объема
(pF – граничный импульс Ферми)
Введем параметр x = pF/mec. При x << 1 электроны нерелятивистские, при x >> 1 – релятивистские.
Чандрасекаровский предел массы
Слайд 18
Считается, что белые карлики - это обнажившееся ядро
звезды, находившейся до сброса наружных слоев на ветви сверхгигантов.
Когда оболочка планетарной туманности рассеется, ядро звезды, находившейся до этого на ветви сверхгигантов, окажется в верхнем левом углу диаграммы ГР. Остывая, оно переместится в верхний угол диаграммы для белых карликов. Ядро будет горячее, маленькое и голубое с низкой светимостью - это и характеризует звезду как белый карлик. Белые карлики состоят из углерода и кислорода с небольшими добавками водорода и гелия, однако у массивных сильно проэволюционировавших звезд ядро может состоять из кислорода, неона или магния. Ядерные реакции в белом карлике не идут. Для белых карликов существует зависимость "масса-радиус", причем чем больше масса, тем меньше радиус.
Слайд 19
Сравнение свойств белого карлика Сириус В с Землей
и Солнцем
Слайд 20
Перенос излучения в звездах
Перенос энергии из недр звезды
к ее поверхности может осуществляться различными механизмами: излучением, электронной
теплопроводностью, конвекцией. Для нормальных звезд в большинстве случаев этот перенос обусловлен лучистой теплопроводностью.
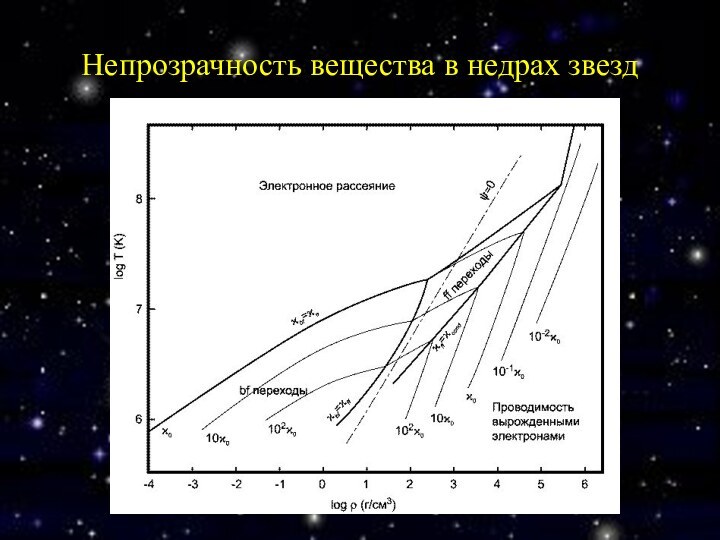
Лучистый перенос представляет собой диффузионный процесс. Фотоны многократно рассеиваются, поглощаются и переизлучаются (за счет томсоновского рассеяния и тормозного механизма излучения). Коэффициент диффузии равен D = cl/3, где l – средняя длина свободного пробега фотонов, l ~ 1/κρ (κ – «непрозрачность», κ = α/ρ). Время диффузии tD ~ R2/D. Для Солнца время диффузии фотонов составляет около миллиона лет.
При некоторых условиях (градиент температуры выше адиабатического) радиальное распределение плотности оказывается неустойчивым и возникает конвекция. Внешняя конвективная зона имеется на Солнце.
Слайд 21
Непрозрачность вещества в недрах звезд
Слайд 23
Уравнения звездной структуры
X, Y, Z – весовые доли
элементов: водорода, гелия и др.
Слайд 25
Соотношение масса – светимость
Из уравнений, описывающих структуру нормальных
звезд, можно найти связь между массой и светимостью звезды.
Для звезд с массой порядка солнечной
Характерное время жизни звезды на главной последовательности
(ηn – эффективность ядерных реакций (~ 0.007), Mc – масса ядра звезды). Массивные звезды эволюционируют быстрее.
Слайд 27
Эддингтоновский предел светимости
Этот предел определяется равенством силы светового
давления на электрон и силы притяжения протона звездой.
Слайд 28
Ядерные источники энергии звезд
Если бы Солнце светило только
за счет запасов тепловой энергии, то их хватило бы
на ~ 30 млн. лет.
При типичных температурах средняя кинетическая энергия частиц в центре звезды ~ 1 кэВ. В то же время для преодоления кулоновского отталкивания двух протонов необходима энергия ~ 1 МэВ. При максвелловском распределении доля частиц с такой энергией ~ e-1000 ≈ 10-430. В Солнце всего 1057 частиц, т.е. классическая вероятность взаимодействия двух протонов пренебрежимо мала. Однако, вероятность такого взаимодействия значительно увеличивается с учетом законов квантовой механики за счет туннельного эффекта.
Слайд 30
Ядерные реакции в звездах
Основные типы ядерных реакций в
звездах – это так называемый протон-протонный и углеродный (CNO)
циклы. Первый доминирует при T < 20 млн. K, второй – при более высоких температурах.
В обоих случаях в конечном счете из 4-х протонов образуется одно ядро гелия. При этом выделяется энергия
(4Mp – MHe)c2 = 28.3 МэВ.
Минимальная масса звезды, при которой возможны ядерные реакции, ~ 0.1 солнечной.
Слайд 31
Ядерные реакции в звездах:
протон-протонный цикл
Вторая цепочка дает
побочные продукты:
Последний распад дает нейтрино высоких энергий (8–9 МэВ).
Слайд 32
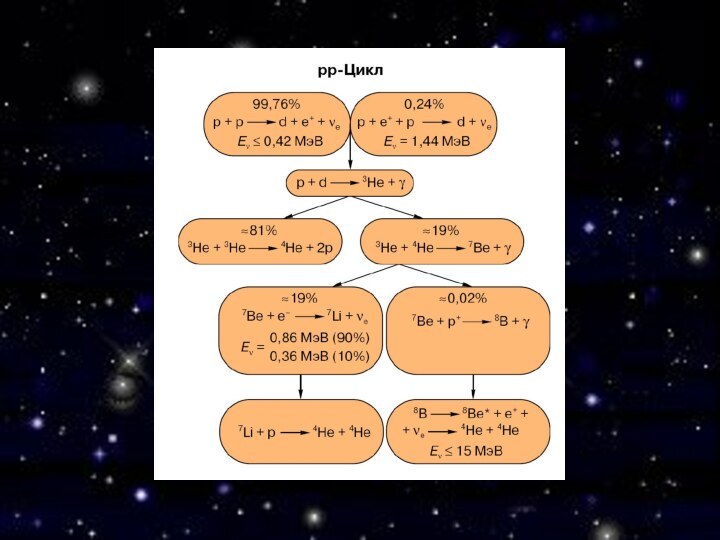
Основные цепи реакций превращения водорода в гелий, характерные
для звезд с массами, близкими к солнечным. Две реакции,
показанные слева вне основного пути обычно не относятся к pp-циклу, а существенны только при точном подсчете количества высокоэнергетических нейтрино. С точки зрения энерговыделения существенны только первые две цепочки.
Слайд 34
Ядерные реакции в звездах:
углеродный (CNO) цикл
Углерод здесь
выступает в роли катализатора. Количество энергии, выделяемой в обоих
циклах, примерно одинаково.
Слайд 36
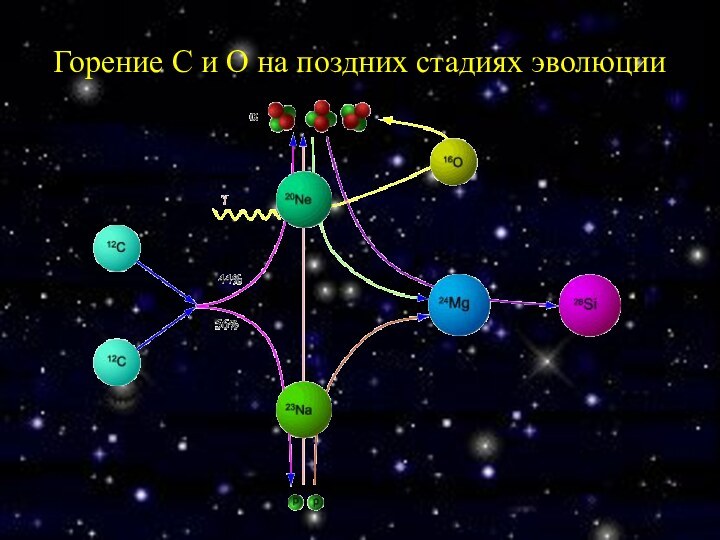
Горение C и O на поздних стадиях эволюции
Слайд 37
Горение кремния и образование элементов до железного пика
Слайд 39
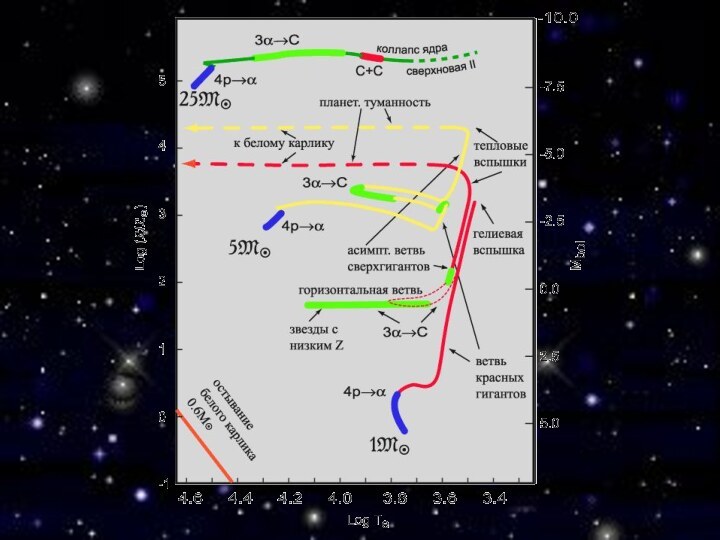
Эволюция звезд после главной последовательности
При достаточно больших массах
звезд (> 0.5 солнечной) нет глобального перемешивания, поэтому водород
в центре постепенно истощается. Появляется слоевой источник энергии и изотермическое гелиевое ядро. Звезда начинает разбухать и ее радиус увеличивается в десятки раз. На диаграмме Гецшпрунга – Рассела звезда переходит в область красных гигантов.
Слайд 46
Планетарные туманности
Планетарная туманность является сброшенными верхними слоями
сверхгиганта. Свечение обеспечивается возбуждением газа ультрафиолетовым излучением центральной звезды.
Туманность излучает в оптическом диапазоне, газ туманности нагрет до температуры порядка 10000 К.
Слайд 48
Схема эволюции одиночной звезды
Слайд 49
Сверхновые
Подавляющее большинство сверхновых (SN) можно классифицировать в один
из двух типов: SNI и SNII. Главный признак, по
которому ведется классификация, – наличие в оптическом спектре эмиссий водорода (тип SNI) или их отсутствие (тип SNII). Имеются различия в кривых блеска. Физически SNI и SNII – также разные типы объектов. Механизмы вспышек сверхновых до конца не ясны.
Слайд 50
При достаточно большой плотности ядра давление электронного вырожденного
газа становится неспособным противостоять дальнейшему сжатию, и свободные электроны
соединяются с протонами, образуя нейтроны и испуская нейтрино. Нейтрино, которые испускаются прямо из ядра, способствуют дальнейшей потере им энергии и еще более быстрому коллапсу. Ядро коллапсирует столь стремительно (за время порядка секунды), что наружные слои звезды отстают от него. Когда ядро уменьшится до размера около 10 км, нейтронный газ станет вырожденным и резко остановит дальнейшее сжатие. Направленная наружу ударная волна увлечет оставшийся материал оболочки за собой, сжимая и нагревая его. Конечным результатом будет формирование нейтронной звезды или черной дыры в ядре и полный разрыв остатка звезды с высвобождением энергии порядка 1053 эрг в нейтрино и 1051 эрг в кинетической и световой энергии.
Слайд 54
Мультипликация NASA, показывающая взрыв звезды как сверхновой и
превращение ее в пульсар.
Слайд 56
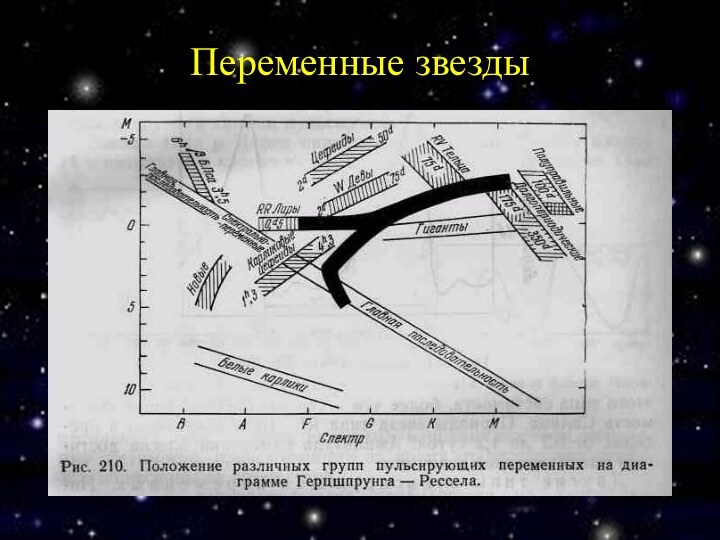
Соотношение период-светимость
При определенных условиях в звезде развиваются автоколебательные
процессы, приводящие к периодическому изменению ее светимости. Механизм основан
на изменении состояния ионизации гелия и, соответственно, - коэффициента непрозрачности (С.А. Жевакин).
Для цефеид существует связь между периодом и светимостью. Это позволяет достаточно надежно оценивать расстояния до этих звезд, что делает их «маяками Вселенной».
Слайд 57
Нейтронные звезды
При больших плотностях из-за вырождения могут идти
процессы нейтронизации:
Пороговые энергии для разных элементов различны.
При массах ядра
звезды больше Чандрасекаровского предела (~ 1.2 массы Солнца), но меньше ~ 2.5 солнечных после исчерпания значительной части ядерного горючего происходит катастрофический коллапс и образуется нейтронная звезда (размер ~ 10 км). Нейтронные звезды были открыты в 1967 г. (пульсары).
Слайд 58
Черные дыры
Гравитационный радиус (радиус Шварцшильда)
Для Солнца rg =
3 км.
Слайд 60
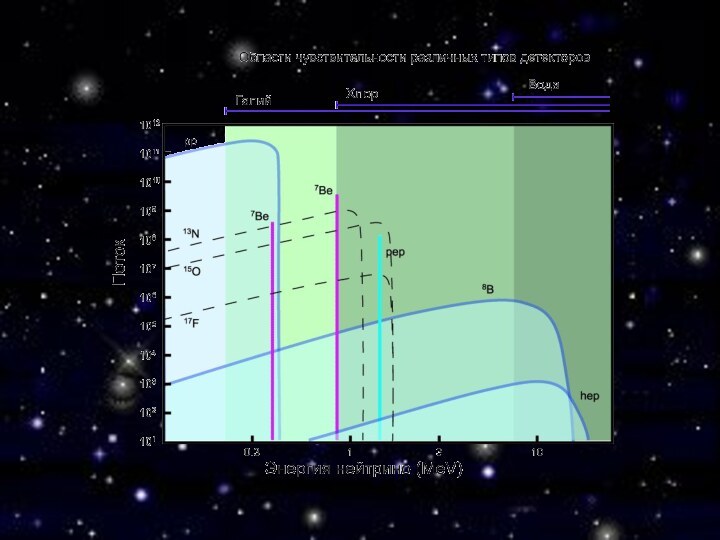
Проблема солнечных нейтрино и нейтринная астрономия
Количество нейтрино, излучаемое
Солнцем за секунду, определяется только светимостью Солнца, т.к. при
выделении 26.7 МэВ рождается 2 нейтрино. Выполненные к настоящему времени измерения дают величину потока нейтрино от Солнца заметно меньше ожидаемой.
Слайд 62
Баксанская нейтринная обсерватория
Подземная лаборатория галлий-германиевого нейтринного телескопа (ГГНТ)
для детектирования солнечных нейтрино с мишенью из 60 тонн
металлического галлия, расположенного на расстоянии 3,5 км от входа в тоннель.
Слайд 63
GALLEX
Result: 77.5 SNU
SSM prediction: 129 SNU
Слайд 65
Нейтринная обсерватория в Садбери
Нейтринная обсерватория в Садбери (Онтарио,
Канада) (Sudbury Neutrino Observatory (SNO)) была построена в шахте
на глубине 2070 метров. 1000 тонн сверхчистой тяжелой воды (D2O) залито в акриловый сосуд диаметром 12 метров. Черенковское излучение регистрируется 9600 фотоумножителями. Детектор погружен в сверхчистую обычную воду, которая находится в бочкообразной полости диаметром 22 метра и высотой 34 метра, выкопанной в скале. За сутки детектор регистрирует около 10 нейтринный событий.
Нейтринные потоки "борных" нейтрино, детектировались с помощью реакций (первая реакция (СС), протекающая с участием заряженных токов, чувствительна только к электронным нейтрино; вторая (NC), протекающая с участием нейтральных токов чувствительна ко всем нейтрино; упругое рассеяние (ES) чувствительно ко всем ароматам нейтрино, но к мюонным и тау в меньшей степени):
Слайд 66
Нейтринная обсерватория в Садбери