- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Фракталы в биологии
Содержание
- 2. Приближенные к фракталам структуры, как мы
- 5. Фракталы и теория самоорганизации как методы изучения
- 6. Во второй половине нашего века в
- 7. Принципы нелинейности и альтернативы выбора развития
- 8. Фрактальная геометрия дала возможность сжатого математического описания
- 9. Исследования фракталов и хаоса в биологии постепенно
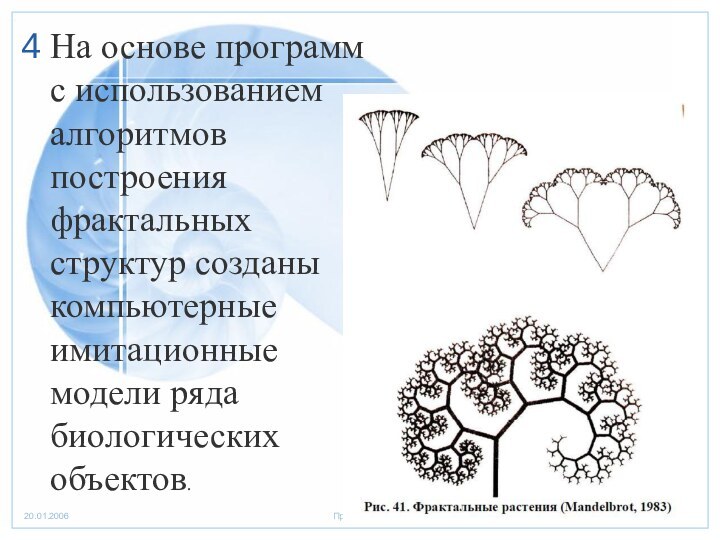
- 10. На основе программ с использованием алгоритмов построения фрактальных структур созданы компьютерные имитационные модели ряда биологических объектов.
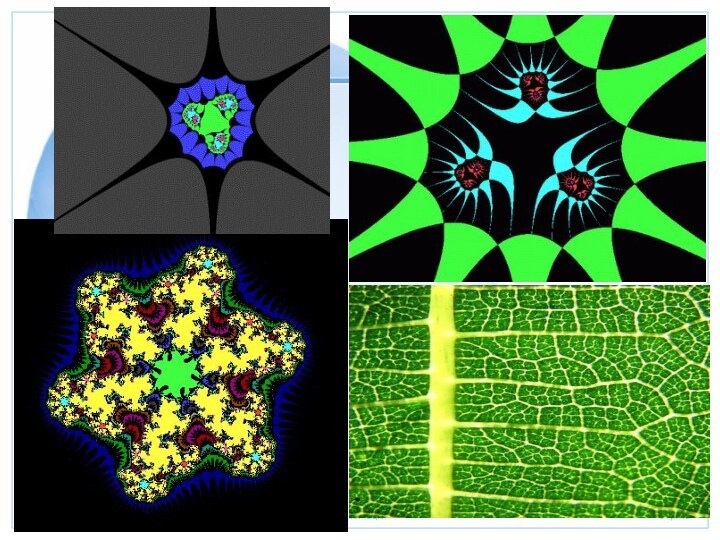
- 11. Биоморфы – одно из практических применений фракталов.
- 12. Термин «биоморф»был предложен Клиффордом Пикуовером, известным
- 13. Биоморфы находятся в комплексной плоскости. Это
- 14. На основании сходства между одноклеточными организмами и
- 17. Скачать презентацию
- 18. Похожие презентации
Приближенные к фракталам структуры, как мы можем заметить, повсеместно встречаются в природе. Неудивительно, если учесть, что одно из свойств фракталов – самоподобность – лежит в основе всего органического и неорганического мира. От атомов и клеточных















Слайд 5 Фракталы и теория самоорганизации как методы изучения биологических
систем
“ Я придумал слово “фрактал”, взяв за основу
латинское прилагательное “fractus”, означающее нерегулярный, рекурсивный, фрагментный”.Бенуа Мандельброт
Слайд 6
Во второй половине нашего века в естествознании
произошли фундаментальные изменения, породившие
так называемую теорию самоорганизации, или
синергетику. Она родилась внезапно, на
пересечении нескольких линий научного исследования.
Самоорганизация – рождение регулярного
предсказуемого поведения в сложной системе,
состоящей из элементов с хаотической динамикой
(т. е. им свойственна многовариантность развития).
Слайд 7
Принципы нелинейности и альтернативы выбора развития любого
процесса, развития системы реализуется и при построении фракталов.
Таким образом,
фракталы позволяют намного упростить сложные процессы и объекты, что очень важно для моделирования, и описать нестабильные системы и процессы и, самое главное, предсказать будущее таких объектов.
Слайд 8
Фрактальная геометрия дала возможность сжатого математического описания биологических
структур и процессов, недоступных для описания языком геометрии Эвклида.
Общая черта фрактальных ветвящихся структур в живой природе – увеличение площади поверхности тела, раздела фаз, максимальное заполнение пространства, что обеспечивает живым организмам более эффективный контакт с окружающей средой. В этом – биологическая функция таких структур, создающих огромное разнообразие биологических систем.Слайд 9 Исследования фракталов и хаоса в биологии постепенно охватывают
все уровни организации живого, от молекул до экосистем.
На
молекулярном уровне это изучение первичной и вторичной структуры ДНК, РНК, белков, других макромолекул и их комплексов, динамики окислительных процессов и т.д. На субклеточном и клеточном уровне исследуются фрактальные свойства пространственной организации мембран, цитоплазмы, ядер, морфология различных клеток и их ассоциаций.
Тканевой уровень фрактальных исследований включает морфологическую организацию и разнообразные гистогенезы (т.е. образование тканей) в норме и патологии, особенно при онкологических заболеваниях.
На уровне органов и организма изучается фрактальная организация дыхательной, сосудистой и других систем животных и растений, множество физиологических и поведенческих реакций организма.
Слайд 10 На основе программ с использованием алгоритмов построения фрактальных
структур созданы компьютерные имитационные модели ряда биологических объектов.
Слайд 12 Термин «биоморф»был предложен Клиффордом Пикуовером, известным ученым
из Исследовательского центра им. Томаса Уотсона фирмы IBM в
Йорктаун-Хейтсе (штат Нью-Йорк). Слово означает «нечто похожее на живой организм». Благодаря поразительному сходству биоморфов с простейшими, Пикоувер был назван «Левенгуком ХХ века». (Антони ван Левенгук, живший в XVII в. нидерландский натуралист, первым соорудивший микроскоп и увидевший в капле воды живые существа).Слайд 13 Биоморфы находятся в комплексной плоскости. Это плоскость,
точка на которой называется комплексным числом и состоит из
двух частей - действительной (координата x) и мнимой (координата y). Такое число записывается так: x+y·i.Строятся путём многочисленных итераций, или последовательных вычислений определённой математической функции, путём повторяющихся математических операций. На каждом шаге итерационного процесса результат предыдущего шага принимается за исходное значение переменной.