- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Функции и их свойства
Содержание
- 2. Функции и их свойствау = f (x)уx0Учитель математики Потеряйкина О.Н.МБОУ СОШ №68г. Хабаровск
- 3. Из истории возникновения функцииПонятие функции уходит своими
- 4. Из истории возникновения функцииВ ДРЕВНЕМ ЕГИПТЕКогда возникли
- 5. Из истории возникновения функцииФРАНЦИЯФРАНСУА ВИЕТ 1540 –
- 6. ГОТФРИД ВИЛЬГЕЛЬМ ЛЕЙБНИЦ 1646 – 1716 гг
- 7. Из истории возникновения функцииЛЕОНАРДО ЭЙЛЕР 1707 -
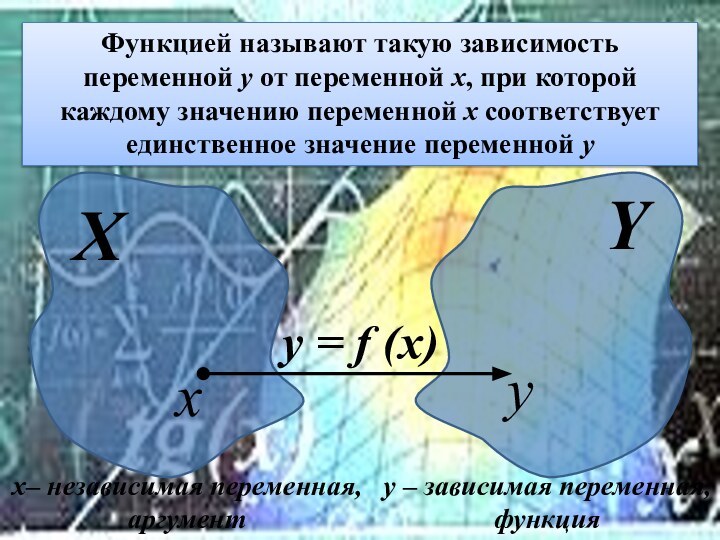
- 8. ХYxyу = f (x)Функцией называют такую зависимость
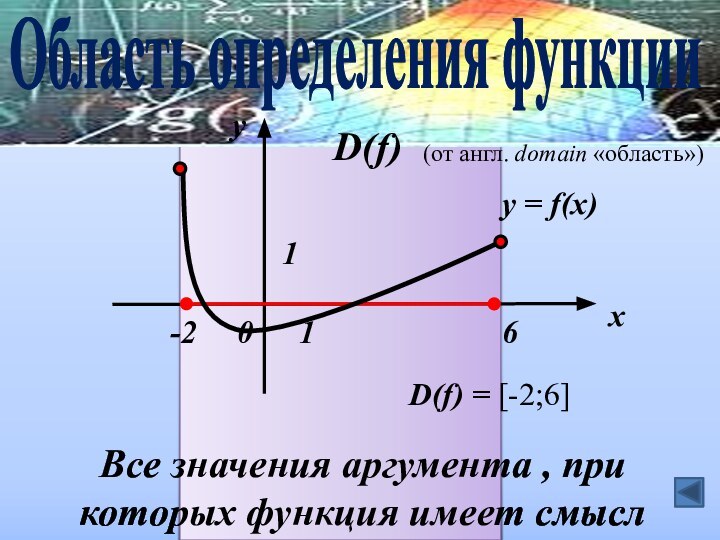
- 9. Область определения функции Область значений функции
- 10. Все значения аргумента , при которых функция
- 11. Область значений функцииВсе значения, которые принимает функция(от англ. codomain «со-область»)Е(f)x01163-2yy = f(x) Е(f) = [-2;3]
- 12. А теперь, ребята, встать Руки медленно поднять,
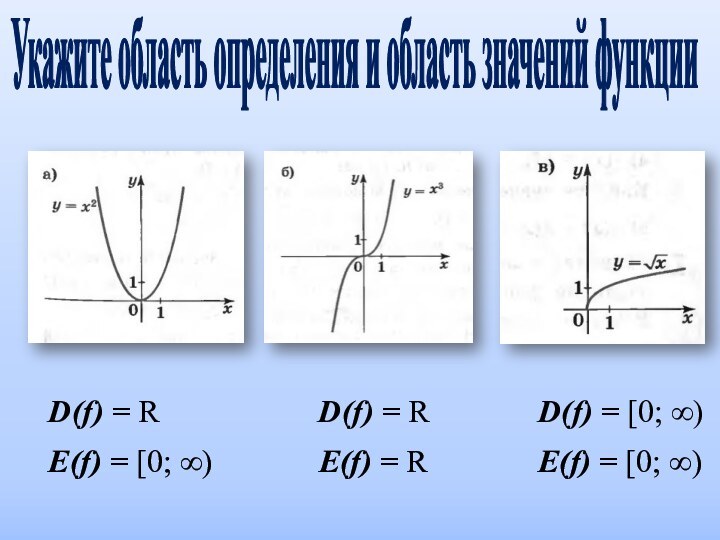
- 13. Укажите область определения и область значений функциив)
- 14. Укажите область определения и область значений функции
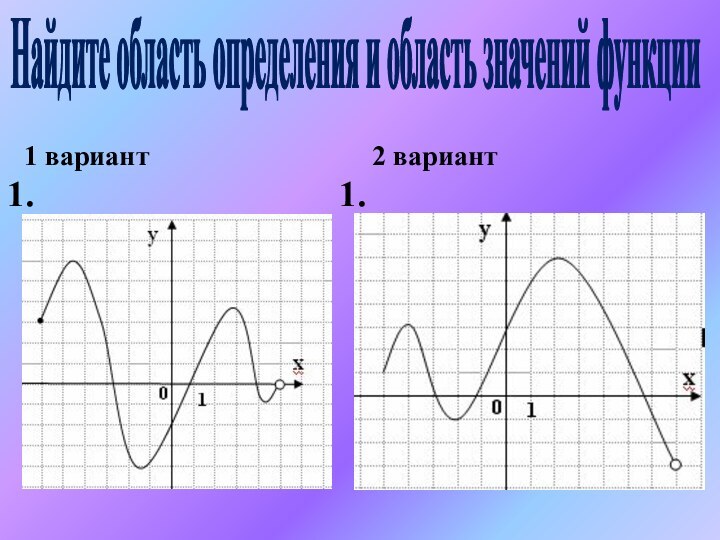
- 15. 1 вариант2 вариантНайдите область определения и область значений функции1.1.
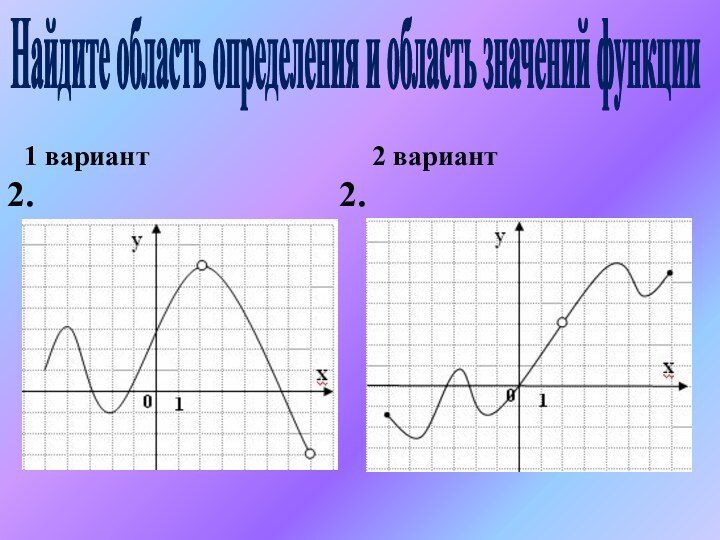
- 16. 1 вариант2 вариантНайдите область определения и область значений функции2.2.
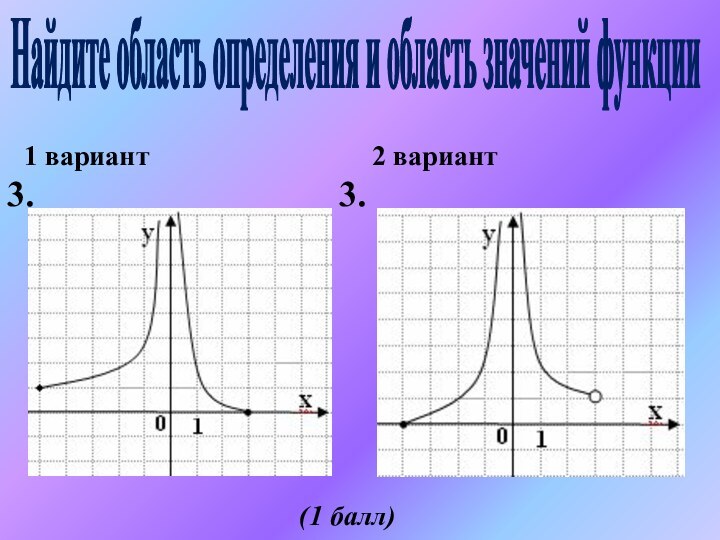
- 17. 1 вариант2 вариантНайдите область определения и область значений функции3.3.(1 балл)
- 18. ,,b = 0a ≥ 01.2.
- 19. Найдите область определения функции1 вариант2 вариантх ϵ
- 20. Оцени свою работу 8 – 10 баллов11 – 13 баллов14 баллов345
- 21. Скачать презентацию
- 22. Похожие презентации








![Функции и их свойства Область значений функцииВсе значения, которые принимает функция(от англ. codomain «со-область»)Е(f)x01163-2yy = f(x) Е(f) = [-2;3]](/img/tmb/12/1139876/065f00324859756be294a3dcbc99612d-720x.jpg)


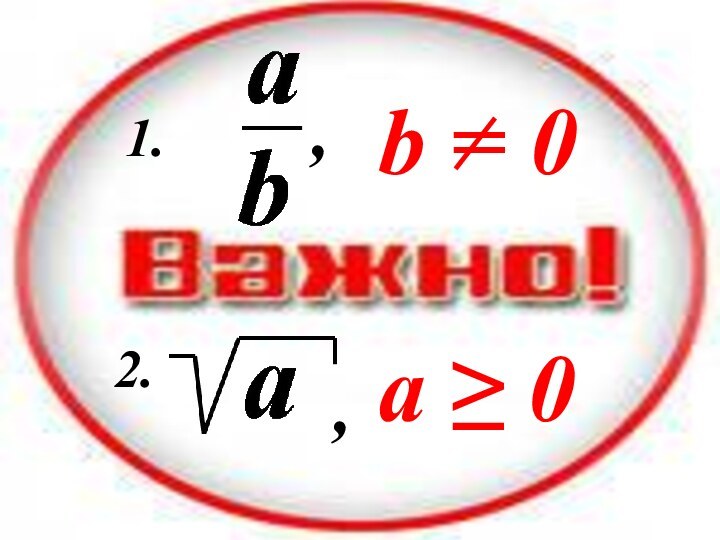



Слайд 3
Из истории возникновения функции
Понятие функции уходит своими корнями
в ту далекую эпоху, когда люди впервые поняли, что
окружающие их явления взаимосвязаны.В ДРЕВНЕМ МИРЕ
Чем больше животных удастся убить на охоте, тем дольше племя будет избавлено от голода
Чем дольше горит костер, тем теплее будет в пещере.
Слайд 4
Из истории возникновения функции
В ДРЕВНЕМ ЕГИПТЕ
Когда возникли первые
цивилизации, началось строительство гигантских пирамид, понадобились писцы, которые учитывали
поступающие налоги, определяли количество кирпичей, необходимое для возведения дворцов.В ДРЕВНЕМ ВАВИЛОНЕ
Чтобы облегчить вычисления, вавилоняне составили таблицы обратных значений чисел, таблицы квадратов и кубов чисел и даже таблицы для суммы квадратов чисел их кубов. Говоря современным языком, это было табличное задание функции y = 1/x.
Слайд 5
Из истории возникновения функции
ФРАНЦИЯ
ФРАНСУА ВИЕТ
1540 – 1603
гг
РЕНЕ ДЕКАРТ 1596 –1650 гг
Разработали единую буквенную
математическую символику.
Слайд 6
ГОТФРИД ВИЛЬГЕЛЬМ
ЛЕЙБНИЦ
1646 – 1716 гг
Из
истории возникновения функции
ГЕРМАНИЯ
Впервые употребил слово «функция»
В печати ввел
с 1694 года. Начиная с 1698 года ввел также термины «переменная» и «константа».
Слайд 7
Из истории возникновения функции
ЛЕОНАРДО ЭЙЛЕР
1707 - 1783
гг
Швейцарский, немецкий и российский математик и механик
В 1748
году дает окончательную формулировку определения функции: «Когда некоторые количества зависят друг от друга таким образом, что при изменении последних и сами они подвергаются изменению, то первые называют функцией вторых».
Слайд 8
Х
Y
x
y
у = f (x)
Функцией называют такую зависимость переменной
у от переменной х, при которой каждому значению переменной
х соответствует единственное значение переменной ух– независимая переменная,
аргумент
у – зависимая переменная,
функция
Слайд 9
Область определения функции
Область значений функции
Нули
функции; промежутки
знакопостоянства
Монотонность
Наибольшее и наименьшее
значения функции
Непрерывность
Четные и нечетные функции
Свойства числовых функций
Слайд 10 Все значения аргумента , при которых функция имеет
смысл
Область определения функции
D(f)
x
0
1
1
6
-2
y
y = f(x)
(от англ. domain «область»)
D(f)
= [-2;6]
Слайд 11
Область значений функции
Все значения, которые принимает функция
(от англ.
codomain «со-область»)
Е(f)
x
0
1
1
6
3
-2
y
y = f(x)
Е(f) = [-2;3]
Слайд 12
А теперь, ребята, встать
Руки медленно поднять,
Пальцы сжать,
Потом
разжать, Руки вниз и так стоять. Наклонитесь вправо, влево. И беритесь вновь
за дело
Слайд 13
Укажите область определения и область значений функции
в)
D(f)
= R
Е(f) = R
D(f) = R
Е(f)
= b D(f) = (∞;0)ᴜ(0; ∞)
Е(f) = (∞;0)ᴜ(0; ∞)
Слайд 14
Укажите область определения и область значений функции
D(f)
= [0; ∞)
Е(f) = [0; ∞)
D(f) =
R Е(f) = R
D(f) = R
Е(f) = [0; ∞)
Слайд 19
Найдите область определения функции
1 вариант
2 вариант
х ϵ R
х ϵ R
х ϵ R
х ϵ R
х ≠ 1,5
х ≠ 2
х ≠ 0,
х ≠ 3
х ≠ - 4
х ≠ 0,
х ˂ 2
х ˂ 1,5
1.
2.
3.
4.
5.
1.
2.
3.
4.
5.