- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по инженерной графике на тему:Лекальные кривые
Содержание
- 2. Лекальные кривыеПри сечении прямого кругового конуса плоскостями,
- 3. Эллипс — замкнутая плоская кривая, сумма расстояний
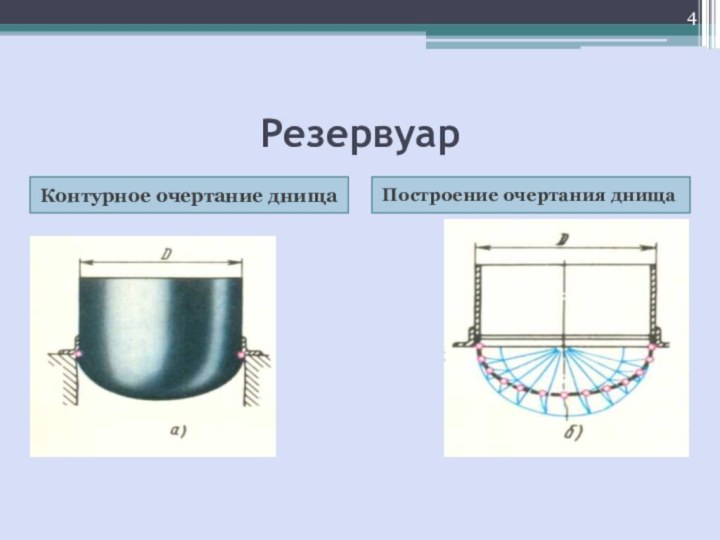
- 4. РезервуарКонтурное очертание днищаПостроение очертания днища
- 5. Парабола — плоская кривая, каждая точка которой
- 6. Гипербола — плоская кривая, состоящая из двух
- 7. Синусоида — плоская кривая, изображающая изменение синуса в зависимости от изменения угла
- 8. СверлоИзображениеЧертеж
- 9. Спираль Архимеда — плоская кривая, которую описывает
- 10. Эвольвента окружности — траектория любой точки прямой линии, перекатываемой без скольжения по окружности.
- 11. Лекальные кривыеЦиклоидальные кривые
- 12. Циклоида — плоская кривая, которую описывает точка
- 13. Эпициклоида — плоская кривая, которую описывает точка
- 14. Гипоциклоида — плоская кривая, которую описывает точка
- 15. Скачать презентацию
- 16. Похожие презентации
Лекальные кривыеПри сечении прямого кругового конуса плоскостями, различно расположенными по отношению к осям конуса, получаются контуры сечения, образующие эллипс, параболу и гиперболу.






















![Презентация. Скороговорки. Звук [п]](/img/tmb/7/670001/07dec6e240c48c4d0d067d476a6dd0b3-210x.jpg)




















