Презентация на тему по теме Кинематика (продолжение)

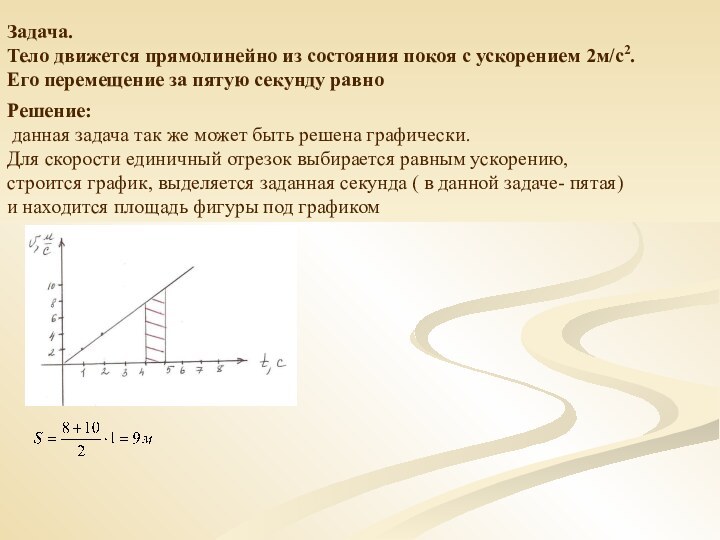
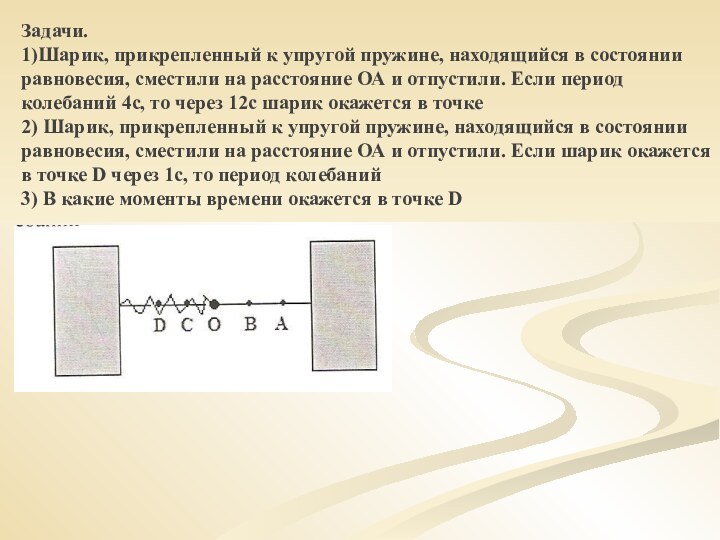
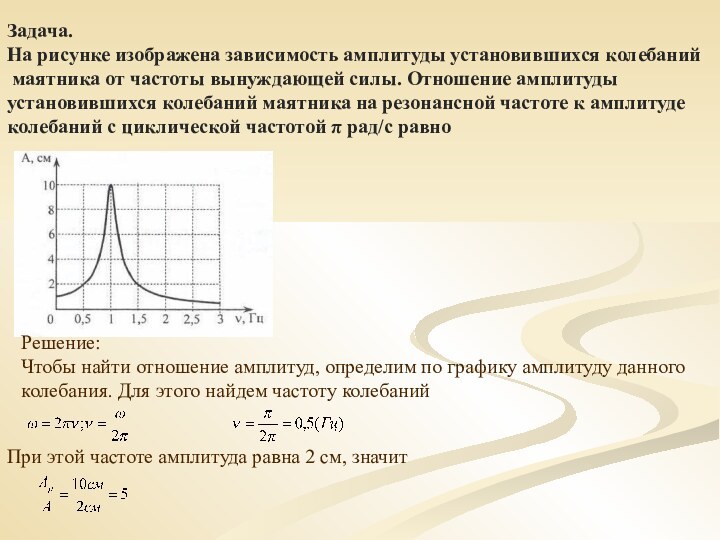
х= 5+8t и у= 4-6t. Скорость точки равна

Решение:
Модуль скорости

любого тела может быть выражен через проекции на оси
координат

Проекции скорости можно найти через уравнения движения двумя способами
сравнивая заданные уравнения с уравнениями в общем виде, определяется
положение проекций ( они стоят перед символом времени)

можно вспомнить, что проекции скорости на оси координат равны
производным соответствующих координат

В данной задаче

,

,

Найдем саму скорость

убегает со
скоростью 10м/с. Время, за которое собака догонит

зайца, если она будет
бежать со скоростью 15м/с

Решение:
Как известно, в момент встречи координаты тел становятся равными.
Напишем уравнения движения для обоих тел ( за начало отсчета выберем
первоначальное положение собаки)

Для зайца:

Для собаки:

При встрече

Решаем уравнение

перемещение тела за промежуток времени
за 4 секунды
2) за 2

секунды

Решение:
1 способ:
По формуле

2 способ ( графический):
Перемещение равно площади фигуры под графиком скорости за заданный
промежуток времени, поэтому
площадь треугольника ( если v0=0)
площадь трапеции ( если v0≠0)

Наибольшее ( наименьшее) перемещение за первую секунду совершило тело

Решение:
Данная задача решается графическим способом.
Там, где за 1 секунду площадь под графиком максимальна,
там и перемещение наибольшее.
Там, где площадь минимальна, там перемещение наименьшее

2м/с2.
Его перемещение за пятую секунду равно

Решение:
данная задача

так же может быть решена графически.
Для скорости единичный отрезок выбирается равным ускорению,
строится график, выделяется заданная секунда ( в данной задаче- пятая)
и находится площадь фигуры под графиком

тела,
начавшего свое движение из начальной координаты равной 14

м.
Координата тела через 12 с равна

Решение:
1-й способ
Тело на разных промежутках времени движется по разному: первые 2 с- равномерно; следующие 2 с- равноускоренно; оставшееся время- равнозамедленно, но с разными ускорениями. Поэтому конечная координата
на каждом участке будет начальной на последующем. Несколько раз используем уравнение координаты

1)

2)

;

;

;

3)

Значит, нам необходимо найти перемещение.
Для решения нужно

помнить, что перемещение равно площади фигуры
под графиком скорости за определенный промежуток времени.
Если внимательно прочитать график, то можно увидеть, что на последнем
участке тело начинает двигаться в обратном направлении после остановки,
поэтому

Значит,

временем по закону v = 10+4t. Средняя скорость за

первые 5с после начала движения равна

Решение:

Из уравнения видим, что это равноускоренное движение, поэтому среднюю скорость можно определить как среднюю арифметическую

Найдем скорости

Значит

а остальную
часть пути со скоростью 60км/ч. Vср на

всём пути …

Решение:
По определению

По условию задачи

Выразим время через промежутки пути

Тогда

36км/ч,
а оставшуюся часть времени со скоростью 54 км/ч.

Средняя скорость
автомобиля

По условию задачи

Решение:

Ответ задан в км/ч, поэтому заданные значения скорости не переводим.
Находим выражения для участков пути:

Тогда

м/с.
Вектор скорости изменяет направление на Δφ = 30о

за 2с.
Нормальное ускорение точки

Решение:

Нормальное ускорение:

Угловая скорость:

Связь между линейной и угловой скоростями

Отсюда

Значит:

угол между
касательной к траектории точки и вектором полного

ускорения равен 60о.
Касательное ускорение равно 5 м/с2. Полное ускорение точки равно
(cos φ =0,5)

Напоминание для неравномерного движения по окружности:
Касательное или тангенциальное ускорение
( всегда направлено по касательной) точки характеризует быстроту изменения модуля скорости
Нормальное ускорение ( всегда направлено к центру) точки характеризует изменение направления линейной скорости
Полное ускорение- геометрическая сумма нормального и касательного ускорений

Решение:
Полное ускорение- гипотенуза, нормальное и касательное ускорения- катеты прямоугольного треугольника.
По определению тригонометрических функций в данной задаче

вид движения
Если векторы скорости и ускорения не коллинеарные,

то движение криволинейное.
Если угол между векторами скорости и ускорения больше 900,
то движение- замедленное по окружности,
если меньше, то движение- ускоренное по окружности

углом 600 к горизонту. Радиус кривизны траектории в ее

верхней точке равен

Решение:

Рассмотрим движение в верхней точке как по дуге окружности, тогда

. значит

В верхней точке скорость направлена горизонтально, поэтому

Тогда

под углом 600.
Кинетическая энергия на высоте 1,95м будет

(g =10 м/с2;cos600=1/2;
sin600=√3/2) (7194 в.22)

Решение:
По закону сохранения энергии мы знаем, что полная энергия в замкнутой
системе остается неизменной в любой момент времени

начальной скоростью 10м/с. Найти скорость мяча через 0,8 секунд

после броска

Решение:

При нахождении любой скорости можно использовать выражение

, где

и

Находим значения проекций скоростей и самой скорости

скоростью 10 м/с. Вектор скорости будет направлен под углом

450 к горизонту через
(g =10 м/с2) (7217 в.20)

Решение:
По горизонтали движение равномерное, значит

По вертикали- равноускоренное

;

Так как угол равен 450, то

значит

v0. в высшей точке траектории, находящейся на высоте h

относительно первоначального положения, тело имеет скорость

Решение.

В верхней точке траектории скорость направлена горизонтально, т.е.

( по горизонтали движение равномерное).

.

угол неизвестен. Из тригонометрии мы знаем, что

Максимальная высота

. Значит

Скорость тела при t= 1с

Решение:
Найдем уравнение зависимости проекции скорости

от времени
Проекция скорости- это производная от координаты

Для t= 1с найдем скорость

v. Длина нити маятника равна
Решение.
Необходимо длину нити выразить через

амплитуду и период.

Для математического маятника

, значит

Найдем период колебаний. Мы знаем, что максимальные значения скорости
и ускорения связаны с амплитудой

).

;

Значит

Ответ::

,

,

,

T и амплитудой xm.
Полная энергия материальной точки равна
Решение:
Полная

энергия

Период пружинного маятника

Найдем жесткость пружины

Значит,

и амплитудой xm.
При прохождении положения равновесия максимальная кинетическая

энергия равна

Решение:
Максимальные значения кинетической и потенциальной энергии равны
между собой

Найдем жесткость пружины через заданные величины

Значит,

равновесия, сместили на расстояние ОА и отпустили. Если период

колебаний 4с, то через 12с шарик окажется в точке
2) Шарик, прикрепленный к упругой пружине, находящийся в состоянии равновесия, сместили на расстояние ОА и отпустили. Если шарик окажется в точке D через 1с, то период колебаний
3) В какие моменты времени окажется в точке D

маятника от частоты вынуждающей силы. Отношение амплитуды
установившихся колебаний

маятника на резонансной частоте к амплитуде
колебаний с циклической частотой π рад/с равно

Решение:
Чтобы найти отношение амплитуд, определим по графику амплитуду данного
колебания. Для этого найдем частоту колебаний

При этой частоте амплитуда равна 2 см, значит

с амплитудой 1,6м и циклической частотой
3,14рад/с. Если начальная

фаза колебаний равна 300, то ускорение точки
через 1с после начала колебаний равно (7189 в.25)

Решение:
Напишем уравнение

Ускорение- это вторая производная от координаты по времени

0,005м. Для удлинения пружины на 0,01м необходима сила 0,2Н.

Уравнение гармонических колебаний в этом случае

Решение:
Гармонические колебания происходят по закону косинуса, т.е.

- амплитуда

Найдем жесткость пружины. По закону Гука

Тогда

Далее находим циклическую частоту

Записываем уравнение

= 0,5sinπt/3. Смещение точки после начала колебаний равно половине

амплитуды через

Для решения этой задачи даже не обязательно иметь числовое значение
амплитуды

В некоторый момент времени смещение точки равно 5 см.

При увеличении фазы колебаний вдвое смещение стало равным 8см.
Амплитуда колебаний равна

Решение:

Уравнение гармонических колебаний х = хm sin ( ωt +φo) ,
обозначим ( ωt +φo) = φ ,
Получаем х = хm sin φ. Составим систему уравнений
5 = хm sin φ,
8 = хm sin2 φ.
Решим систему: Вспомним, что sin2 φ =2 sin φ cos φ .
Разделим второе уравнение на первое, сократим подобные и получим выражение
2 cos φ = 8/5 или cos φ =0,8.
хm =5 / sin φ, найдём sin φ , зная выражение sin2 φ + cos2 φ =1, тогда sin φ = 0,6.
Значит хm =5 /0,6 =8,3см.

закону
х =0,2cos2πt (м). Полная энергия частицы равна

(4157 в.23)

Решение:
Полная энергия частицы

Найдем максимальную скорость

человеком, находящимся под водой, равен 9,35м. Звук от источника

до человека по воздуху идет в 5 раз дольше, чем по воде. Высота источника над водой равна ( vзвука в воде =1483м/с; vзвука в воздухе =340м/с)

Решение:

- расстояние, пройденное звуком над и под водой

Пусть t- время движения звука в воде, тогда в воздухе 5t
Составляем уравнение и находим t

Значит,

приборы, установленные на корабле и принимающие звук на воде,

зарегистрировали на 45 секунд раньше, чем он прошел по воздуху, Взрыв произошел на расстоянии от корабля (скорость звука в воздухе 340 м/с, а в воде 1140 м/с).

Решение:

Расстояние, пройденное звуком по воде и по воздуху, одинаково
Пусть t- время движения звука в воде, тогда (t+45)- время движения по воздуху
v1- скорость звука в воде, v2- воздухе
составляем уравнение и находим время

Значит, расстояние от источника звука до приемника равно

за 6 секунд прошло 4 гребня волны. Расстояние между

первым и третьим гребнями 12 метров. Скорость распространения и длина волны соответственно равны…

Решение:

Между четырьмя гребнями находятся 3 длины волны, т.е. прошло 3 колебания,

тогда период

Между первым и третьим гребнями- 2 длины, значит