- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по физике Механическое движение
Содержание
- 2. Мы живём в мире движущихся объектов
- 7. Мы живём в мире движущихся объектов
- 8. МЕХАНИКАНаука об общих законах движения тел.
- 9. ЗАДАЧА МЕХАНИКИОсновной задачей механики является определение положения тела в любой момент времени.
- 10. КИНЕМАТИКАУстанавливает связь между величинами, характеризующими движение, с помощью формул и графиков.
- 11. Механическое движение -перемещение тела в пространстве относительно других тел с течением времени.
- 12. Материальная точка -тело, размерами которого в данных условиях можно пренебречь.
- 13. ТРАЕКТОРИЯЛиния, по которой движется тело.
- 14. ПУТЬДлина траектории.Обозначается – s, скалярная величина, измеряется в метрах.
- 15. ПеремещениеНаправленный отрезок, соединяющий начало и конец путиОбозначается
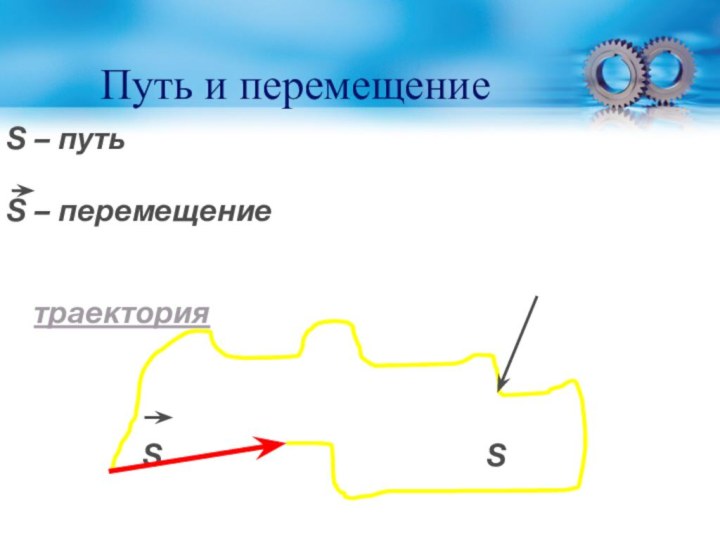
- 16. Путь и перемещениеS – путьS – перемещение
- 17. Путь – скалярная величина и характеризуется только
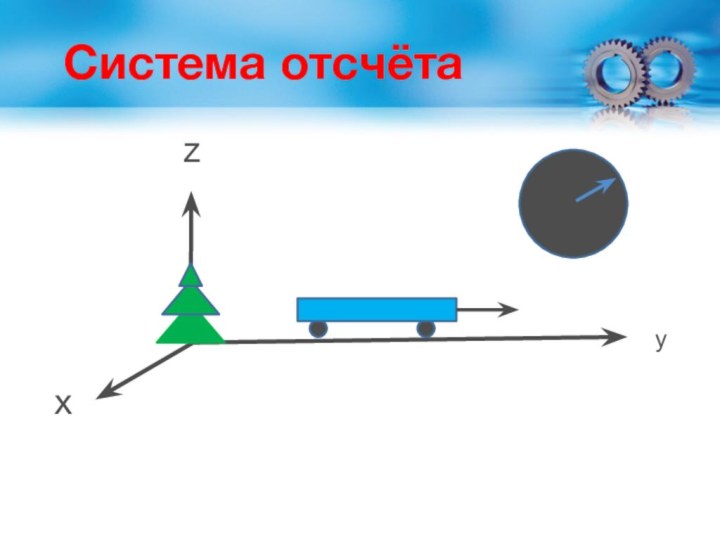
- 18. Система отсчета
- 19. Тележка движется слева направо. Для рассмотрения её движения введём:
- 20. Тело отсчёта
- 21. Добавим систему координат
- 22. Добавим секундомер
- 23. Система отсчёта
- 24. Система отсчетаТело отсчетаСистема координат, связанная с нимПрибор для измерения времени
- 25. Системы координат:
- 26. Проекция вектора
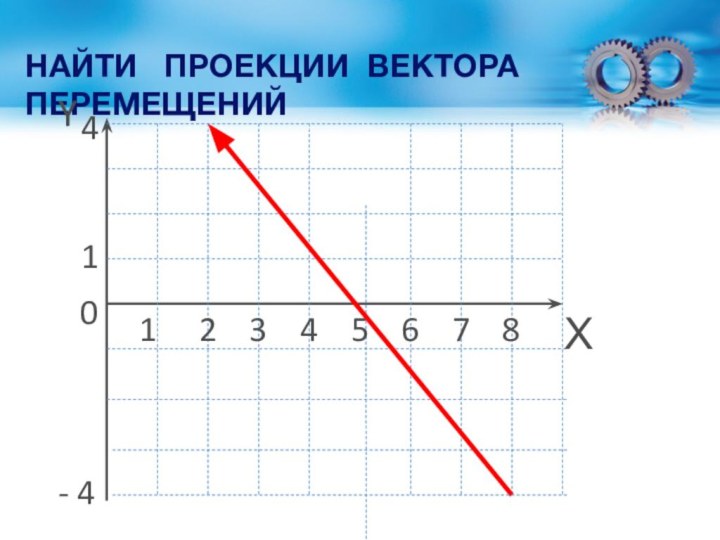
- 29. НАЙТИ ПРОЕКЦИИ ВЕКТОРА ПЕРЕМЕЩЕНИЙ 012345678Х4Y- 41
- 30. ЗАДАЧАНачальные координаты вектора S (8; - 4),
- 31. НАЙТИ ПРОЕКЦИИ ВЕКТОРА ПЕРЕМЕЩЕНИЙ 012345678Х12345Y
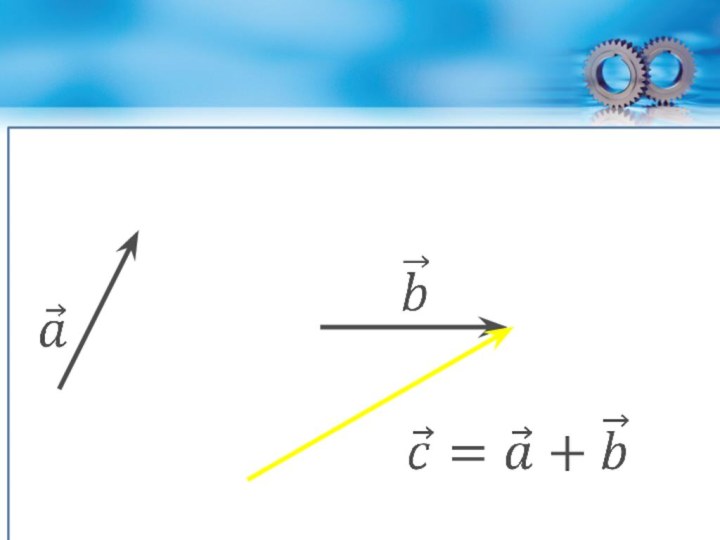
- 32. Правило треугольникаСЛОЖЕНИЕ ВЕКТОРОВ
- 34. Правило параллелограммаСЛОЖЕНИЕ ВЕКТОРОВ
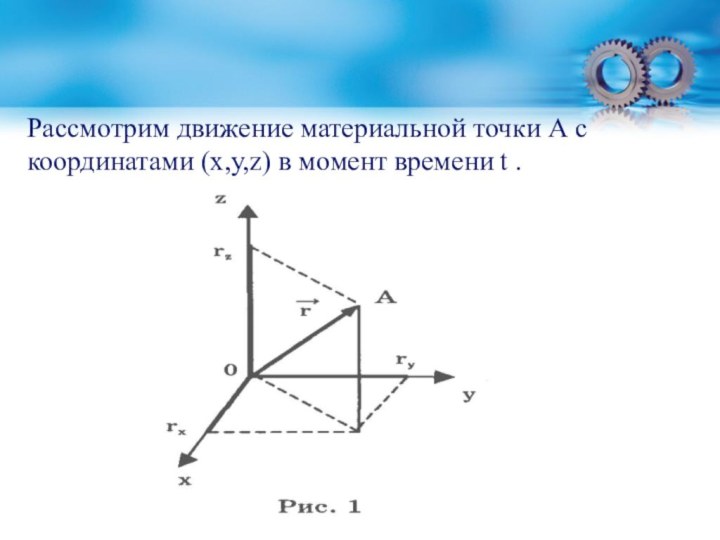
- 36. Рассмотрим движение материальной точки А с координатами (х,у,z) в момент времени t .
- 37. Совокупность координат х(t),
- 40. ВИДЫ ДВИЖЕНИЯ А) по траектории: прямолинейное или
- 43. 1. Что называется механическим движением? Примеры.
- 44. Чтобы определить мгновенную скорость нужно:1. Измерить среднюю
- 45. Закон сложения скоростей υ1 -
- 46. Почему этот текст неправильный: « Поток был
- 47. С К О Р О С Т
- 48. УРАВНЕНИЕ ДВИЖЕНИЯ – определяет положение
- 49. Уравнение равномерного прямолинейного движения
- 50. Запишите уравнение движения
- 51. Графики х=х(t)хt0Скорость численно равна tg α
- 52. Графики v=v(t)vt0
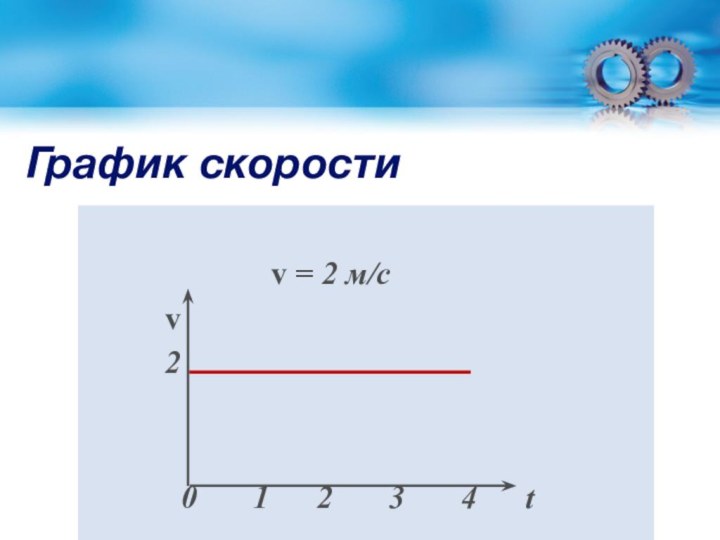
- 53. ГРАФИК СКОРОСТИ
- 55. ГРАФИК КООРДИНАТЫ Х
- 56. График зависимости координаты материальной точки (санок)от времени.Почему
- 58. З А Д А Ч АУравнение движения
- 59. З А Д А Ч АДано:
- 60. График скорости
- 61. График координаты х =
- 62. График пути
- 63. САМОСТОЯТЕЛЬНОУравнение движения тела имеет вид
- 64. В О П Р О С Ы1.
- 65. Равнопеременное движение-движение с постоянным ускорением.Равноускоренное- модуль скорости
- 66. Ускорение- это величина,характеризующая быстроту изменения скорости.
- 68. Скорость при равнопеременном движенииВектор мгновенной скоростиВекторное уравнение
- 71. http:///datas/fizika/Peremeschenie-pri-ravnouskorennom-dvizhenii/0009-009-Dvizhenie-s-postojannym-uskoreniem.jpg
- 72. v0x=v0cosa Определите характер движения, пользуясь рисункоми запишите
- 74. v0x=v0cosa ВСПОМНИМ ИЗУЧЕННОЕv0x=v0cosa vx=v0x+axtvy=v0y+aytsy=v0yt+ayt2/2sx=v0xt+axt2/2x=x0+v0xt+axt2/2y=y0+v0yt+ayt2/2v0x=v0cosa v0x=v0cosa v0x=v0cosa v0x=v0cosa
- 75. Скачать презентацию
- 76. Похожие презентации































































Слайд 9
ЗАДАЧА МЕХАНИКИ
Основной задачей механики является определение положения тела
в любой момент времени.
Слайд 10
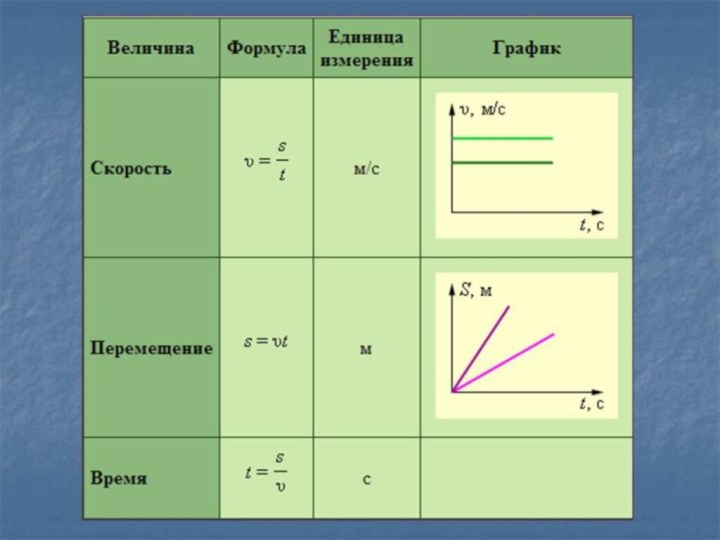
КИНЕМАТИКА
Устанавливает связь между величинами, характеризующими движение, с помощью
формул и графиков.
Слайд 11
Механическое движение -
перемещение тела в пространстве относительно других
тел с течением времени.
Слайд 15
Перемещение
Направленный отрезок, соединяющий начало и конец пути
Обозначается –
s,
векторная величина, измеряется в метрах.
Слайд 17
Путь – скалярная величина и характеризуется только числовым
значением.
Перемещение – векторная величина и характеризуется как числовым значением
(модулем), так и направлением.При движении тела путь может только увеличиваться, а модуль перемещения может как увеличиваться, так и уменьшаться.
Если тело вернулось в начальную точку, его перемещение равно нулю, а путь нулю не равен.
Слайд 30
ЗАДАЧА
Начальные координаты вектора S (8; - 4), конечные
(2; 4).Найдите проекции вектора на оси координат и модуль
вектора S.Дано: Решение
хо = 8 Sх = х – хо Sх = 2 – 8 = - 6
уо = - 4 Sу = у – уо Sу = 4 – ( - 4) = 8
х = 2
у = 4
|S| - ?
Sх - ?
Sу - ?
Ответ: Sх = - 6 Sу = 8 | S | = 10 .
Слайд 37 Совокупность координат х(t), y(t), z(t) в момент времени
t определяет закон движения материальной точки в координатной форме,
тогда положение математической точки можно задать вектором r.
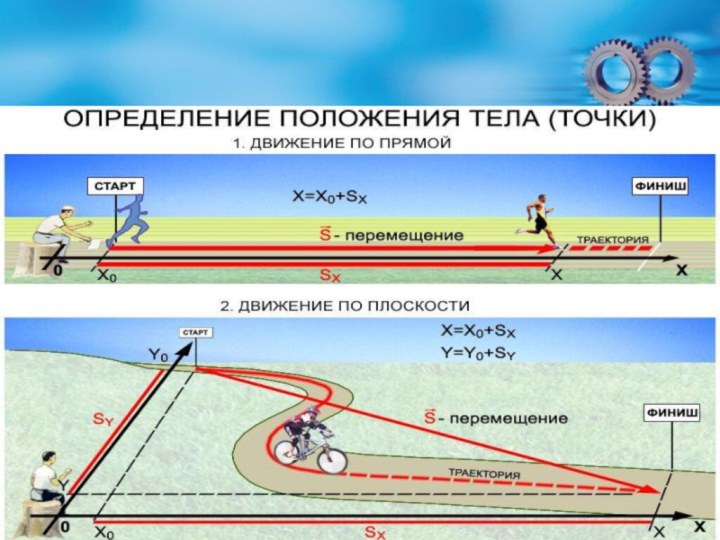
Слайд 40
ВИДЫ ДВИЖЕНИЯ
А) по траектории: прямолинейное или
криволинейное
Б) по скорости: равномерное или
неравномерное
Наиболее простой вид движения:
прямолинейное равномерное (путь равен перемещению, скорость постоянна)
s = x – x0 s = vt (s>0)
Слайд 43 1. Что называется механическим движением? Примеры.
2. В чем заключается основная
задача механики?3. Что называется телом отсчета?
Системой отсчета?
4. Что называется материальной точкой? Примеры.
5. Что называется траекторией? Примеры.
6. Что такое путь? Обозначение, единицы измерения.
7. Что называется перемещением? Примеры.
8. В каком случае модуль перемещения и путь совпадают?
9. От чего зависит знак проекции вектора перемещения?
10. Чем путь отличается от координаты?
Слайд 44
Чтобы определить мгновенную скорость нужно:
1. Измерить среднюю скорость
за интервал времени от t до t+∆t
2. Принять,
что средняя скорость за этот промежуток примерно равна скорости в момент времени t. Чем меньше промежуток времени, тем точнее определена скорость. (∆t→0)
Скорость тела в данной точке траектории в данный момент времени называется мгновенной скоростью.
Слайд 45
Закон сложения скоростей
υ1 - скорость
подвижной системы отсчёта, относительно неподвижной
υ2
= υ1 + υ
υ - скорость тела относительно этой подвижной системы отсчёта
υ2 - скорость того же тела относительно неподвижной системы отсчёта
Слайд 46 Почему этот текст неправильный: « Поток был очень
сильный и Жаба как не старалась не могла догнать
Дюймовочку»?Определите скорость Дюймовочки относительно жабы, если скорость потока 10 см/с, а скорость Жабы 3 см/с.
υ2 = υ1 + υ
Слайд 47
С К О Р О С Т Ь
Скорость
– величина, равная пути пройденному в единицу времени
υ – скорость (м/с)s - путь (м)
t - время (с)
υ (км/ч) : 3,6 = υ (м/с)
Например: 90км/ч : 3,6 = 25 м/с
(за 1ч проходит путь 90км, а за 1с – 25м )
υ =S/ t
Слайд 48
УРАВНЕНИЕ ДВИЖЕНИЯ
– определяет положение (координату)
тела в любой заданный момент времени
х = х0 + vхtх – координата в момент времени t
х0 – начальная координата
vх – проекция скорости на ось Х
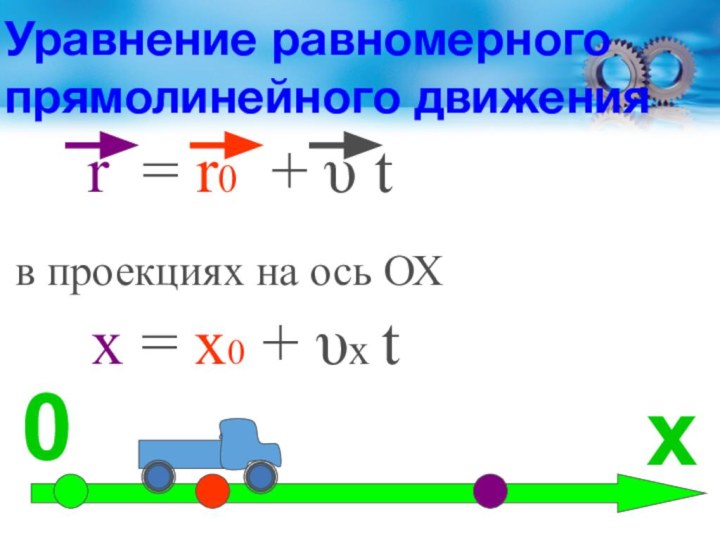
Слайд 49
Уравнение равномерного прямолинейного движения
r = r0 + υ t
в проекциях на
ось ОХ . х = х0 + υх tх
0
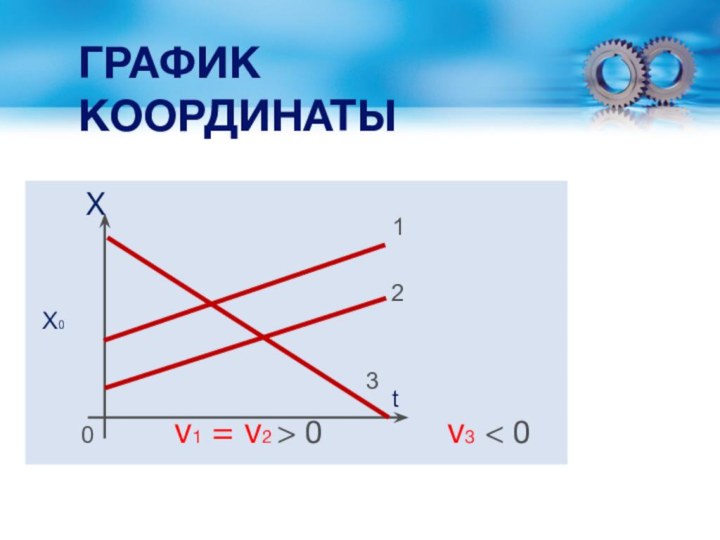
Слайд 56
График зависимости координаты материальной точки (санок)от времени.
Почему санки
можно считать в данной задаче материальной точкой?
Опишите характерные особенности
движения: в каких направлениях двигалась точка относительно оси ОХ в различные интервалы времени.Постройте графики проекции скорости и пути от времени, то есть υх =υх(t) и s=s(t).
с
х
Слайд 58
З А Д А Ч А
Уравнение движения тела
имеет вид
х = 2t – 1Найти: а) начальную координату
б) координату через 1с движения
в) путь, пройденный за 1с
Построить графики зависимости координаты, пути и скорости
от времени
Слайд 59
З А Д А Ч А
Дано:
Решение
х = 2t – 1 Уравнение движения
х0 - ? х = х0 +vt
х(1) - ? а) х0 = - 1м (нач. координата, t=0 )
s (1) - ? б) х(1)=2·1-1=1м (коорд. при t=1с )
Графики в) s = x – x0 s = vt
x(t) s=x(1) – x0 = 1 – (-1) = 2м
v(t), s(t) v=2м/с s=2·1=2м (II способ)
Слайд 63
САМОСТОЯТЕЛЬНО
Уравнение движения тела имеет вид
(I) х = 3t + 2 (II) x = 4 – 2t
(III) x = 1,5t + 4 (IV) x = 3 – t
Найти: а) начальную координату
б) координату через 2с движения
в) путь, пройденный за 2с
Построить графики зависимости координаты, пути и скорости от времени
Слайд 64
В О П Р О С Ы
1. Какое
движение называется прямолинейным?
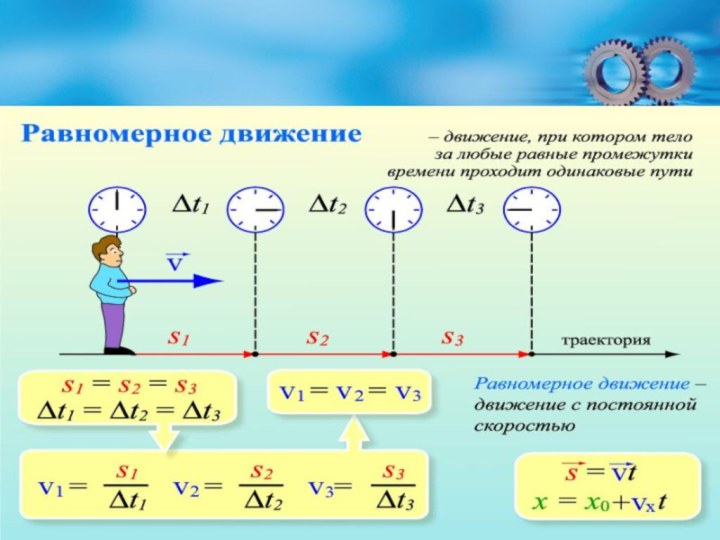
2. Какое движение называется равномерным?
3. Что называется
скоростью?4. В каком случае скорость положительна?
5. В каком случае скорость отрицательна?
6. В каких единицах измеряется скорость?
7. Как перевести км/ч в м/с ?
8. Назовите уравнение равномерного движения.
9. Какие величины не меняются в процессе движения?
10. Какие величины изменяются в процессе движения?
11. Что является графиком равномерного движения?
12.По какой формуле вычисляется путь?
Слайд 65
Равнопеременное движение-движение с постоянным ускорением.
Равноускоренное- модуль скорости увеличивается
с течением времени.
Равнозамедленное- модуль скорости уменьшается с течением времени.
Движение
с постоянным ускорением совершается в одной плоскости
Слайд 68
Скорость при равнопеременном движении
Вектор мгновенной скорости
Векторное уравнение
при
движении
на плоскости эквивалентно
двум уравнениям
для проекций вектора
на координатные оси
Слайд 71
http:///datas/fizika/Peremeschenie-pri-ravnouskorennom-dvizhenii/0009-009-Dvizhenie-s-postojannym-uskoreniem.jpg
Слайд 72
v0x=v0cosa
Определите характер движения, пользуясь рисунком
и запишите формулы
для расчета v и s
v0x=v0cosa
v0x=v0cosa
v0x=v0cosa
v0x=v0cosa
v0
v0
v0
v0
а
а
а
а
х
х
х
х
0
0
0
0
v0x=v0cosa
v0x=v0cosa
v0x=v0cosa
v0x=v0cosa
равноускоренное
равноускоренное
равнозамедленное
равнозамедленное
v= v0 + at
-v = -v0 - at
-v = -v0+at
v =v0 - at
s=v0t+at2/2
-s= -v0t+at2/2
-s = -v0t- at2/2
s= v0t -at2/2
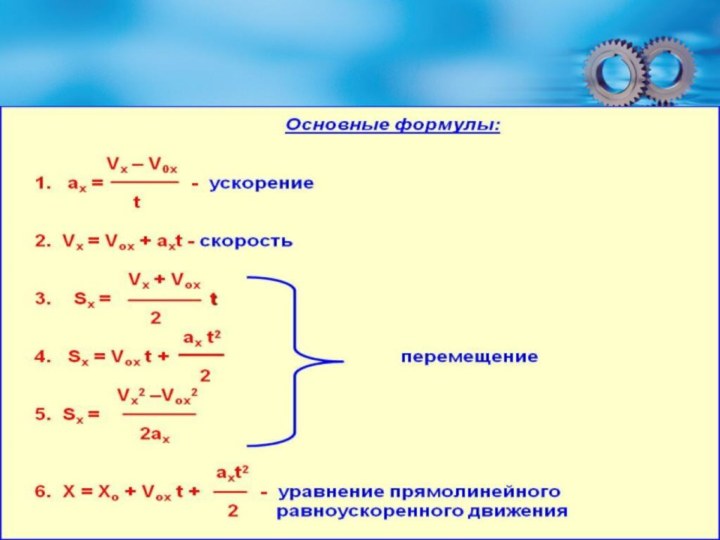
Слайд 74
v0x=v0cosa
ВСПОМНИМ ИЗУЧЕННОЕ
v0x=v0cosa
vx=v0x+axt
vy=v0y+ayt
sy=v0yt+ayt2/2
sx=v0xt+axt2/2
x=x0+v0xt+axt2/2
y=y0+v0yt+ayt2/2
v0x=v0cosa
v0x=v0cosa
v0x=v0cosa
v0x=v0cosa
Какое
движение называется
равноускоренным ?
Определение ускорения.
Физический смысл ускорения.
Формула проекции скорости
приравноускоренном движении
Формула проекции перемещения
при равноускоренном движении
v0x=v0cosa
Формула координаты
при равноускоренном движении





























