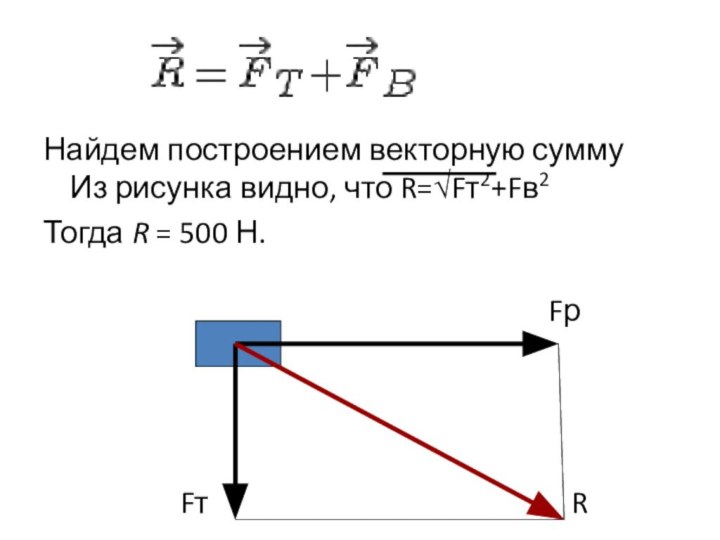
решения этой задачи. Предлагается решение с использованием графика зависимости
проекции скорости поезда от времени. Ось ОХ направляем по ходу движения поезда, часы включаем в момент его отправления.
Обозначения: t – время, на которое опоздал пассажир;
t1 и t2 – промежутки времени, причём t1 > t2;
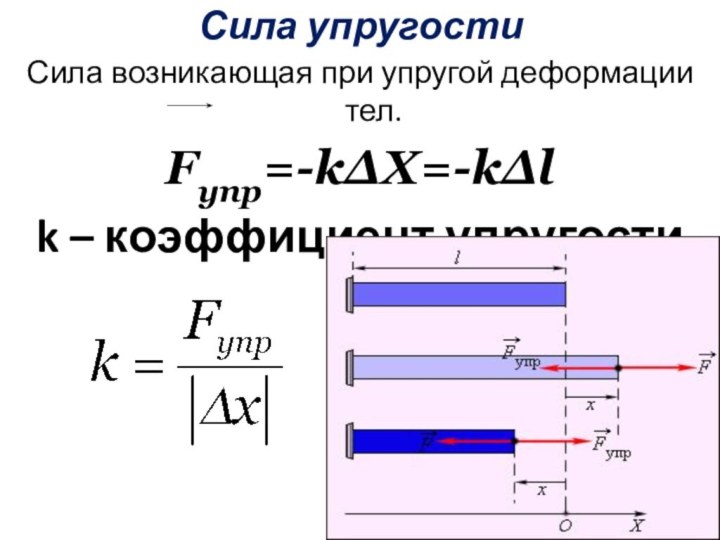
а –ускорение поезда,
V1 – скорость начала предпоследнего вагона,
V2 – скорость конца предпоследнего (начала
последнего) вагона;
V3 – скорость конца последнего вагона.
Тогда V1 =a*t, V2 =a*(t +t1), V3 = a*(t +t1 +t2), но так как площади трапеций равны то получаем выражение
((V1 + V2)/2) *t1 = ((V2 +V3)/2) *t2
После подстановки и преобразований получим ответ:
t = (2*t1*t2 +t22-t12)/2*(t1-t2).
t2
V
t
t
1
o
V
1
V
2
V
3
tс
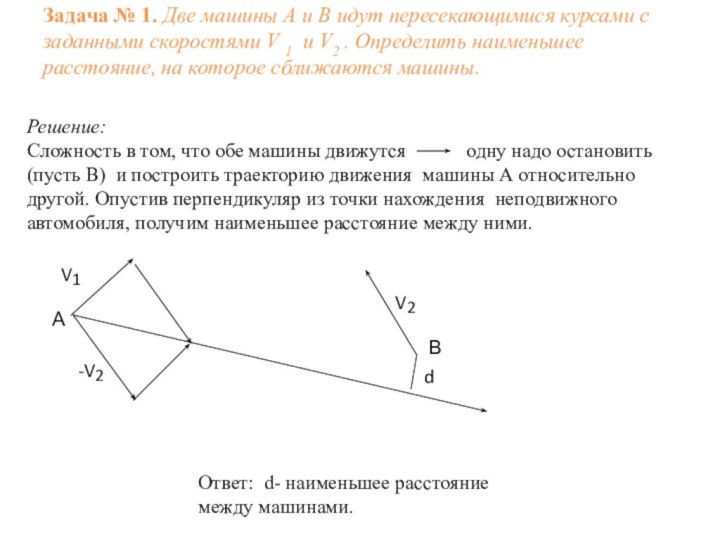
Задача № 2. Когда опоздавший пассажир вбежал на платформу , мимо него за время t 1 прошел предпоследний вагон поезда. Последний вагон прошел мимо пассажира за время t2 . На сколько опоздал пассажир к отходу поезда? Движение поезда считать равноускоренным, длина вагонов одинаковая.
Решение: