параллельно линии её действия, при этом нужно добавить пару
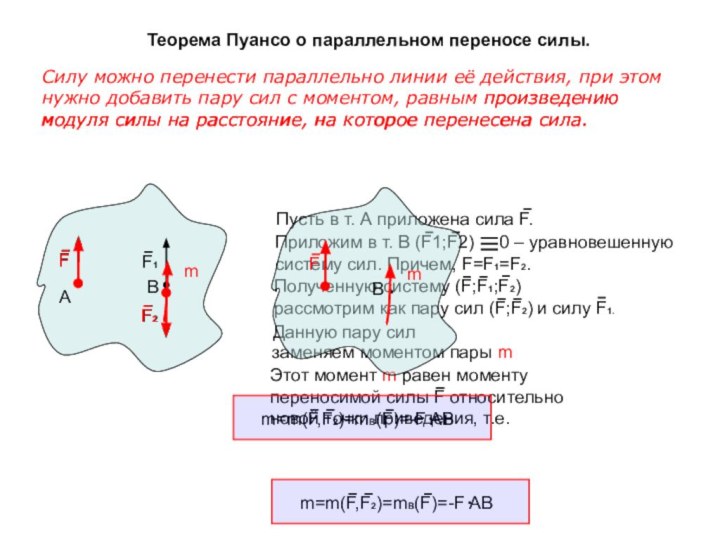
сил с моментом, равным произведению модуля силы на расстояние, на которое перенесена сила.Пусть в т. А приложена сила F.
А
F
Приложим в т. В (F1;F2) 0 – уравновешенную систему сил. Причем, F=F1=F2.
В
рассмотрим как пару сил (F;F2)
и силу F1.
Данную пару сил
.
m
F1
F2
Полученную систему (F;F1;F2)
заменяем моментом пары m
F
F2
m=m(F,F2)=mB(F)=-F AB
Этот момент m равен моменту переносимой силы F относительно новой точки приведения, т.е.
модуля силы на расстояние, на
произведению
которое перенесена сила.
В
F
m
.
m=m(F,F2)=mB(F)=-F AB