Слайд 2
Содержание
-Гравитационные силы
-Обратная задача механики
-Закон всемирного тяготения
-Гравитационная постоянная
-Силы
всемирного тяготения в природе
-Сила тяжести
-Ускорение свободного падения
-При
удалении от Земли
-Луна
-Человек на Луне
-Задача
Слайд 3
Гравитационные силы
Закон всемирного тяготения был открыт И. Ньютоном в
1682 году.
Еще в 1665 году 23-летний Ньютон высказал предположение, что силы, удерживающие Луну на ее орбите, той же природы, что и силы, заставляющие яблоко падать на Землю. По его гипотезе между всеми телами Вселенной действуют силы притяжения (гравитационные силы), направленные по линии, соединяющей центры масс У тела в виде однородного шара центр масс совпадает с центром шара.
Слайд 4
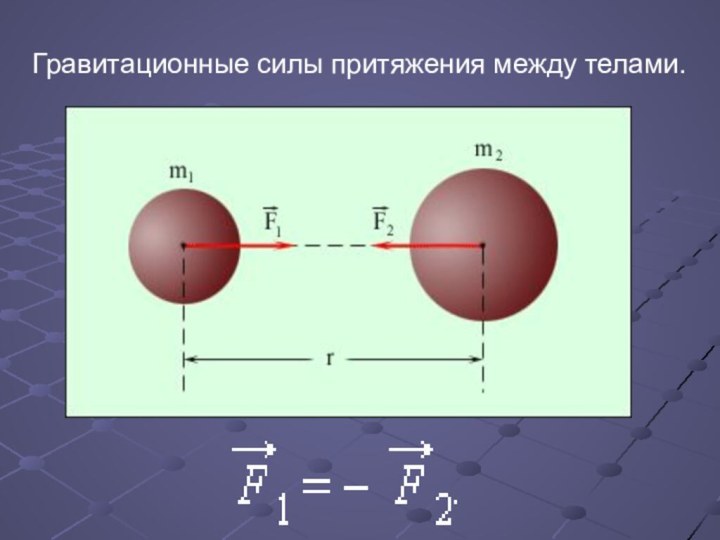
Гравитационные силы притяжения между телами.
Слайд 5
Обратная задача механики
В последующие годы Ньютон пытался найти
физическое объяснение законам движения планет и дать количественное выражение
для гравитационных сил. Зная как движутся планеты, Ньютон хотел определить, какие силы на них действуют. Такой путь носит название обратной задачи механики: определить действующие на тело силы, если известно, как оно движется. Решение этой задачи и привело Ньютона к открытию закона всемирного тяготения.
Слайд 6
Закон всемирного тяготения
Все тела притягиваются друг к другу
с силой, прямо пропорциональной их массам и обратно пропорциональной
квадрату расстояния между ними:
Слайд 7
Гравитационная постоянная
G = 6,67·10–11 Н·м2/кг2 (СИ).
Коэффициент пропорциональности G одинаков для всех
тел в природе. Его называют гравитационной постоянной
Слайд 8
Силы всемирного тяготения в природе
Многие явления в природе
объясняются действием сил всемирного тяготения. Движение планет в Солнечной
системе, движение искусственных спутников Земли, траектории полета баллистических ракет, движение тел вблизи поверхности Земли – все эти явления находят объяснение на основе закона всемирного тяготения и законов динамики.
Слайд 9
Сила тяжести
Одним из проявлений силы всемирного тяготения является
сила тяжести. Так принято называть силу притяжения тел к
Земле вблизи ее поверхности
где g – ускорение свободного падения у поверхности Земли
Слайд 10
Ускорение свободного падения
g – ускорение свободного падения у
поверхности Земли :
Слайд 11
При удалении от Земли
При удалении от поверхности Земли
сила земного тяготения и ускорение свободного падения изменяются обратно
пропорционально квадрату расстояния r до центра Земли.
Слайд 12
Здесь показаны изменения силы тяготения, действующей на космонавта
в космическом корабле при его удалении от Земли. Сила,
с которой космонавт притягивается к Земле вблизи ее поверхности, принята равной 700 Н
Слайд 13
Луна
Собственное гравитационное поле Луны определяет ускорение свободного падения
gЛ на ее поверхности. Масса Луны в 81 раз меньше
массы Земли, а ее радиус приблизительно в 3,7 раза меньше радиуса Земли
Слайд 14
Человек на Луне
В условиях такой слабой гравитации оказались
космонавты, высадившиеся на Луне. Человек в таких условиях может
совершать гигантские прыжки. Например, если человек в земных условиях подпрыгивает на высоту 1 м, то на Луне он мог бы подпрыгнуть на высоту более 6 м
Слайд 15
Задача
Два тела массой m1 = m и m2 = 2m
падают в безвоздушном пространстве. Сравните ускорения a1 и a2
этих тел.
a1 = 2a2
a1 = a2
a2 = 2a1
a1 = 4a2