Слайд 2
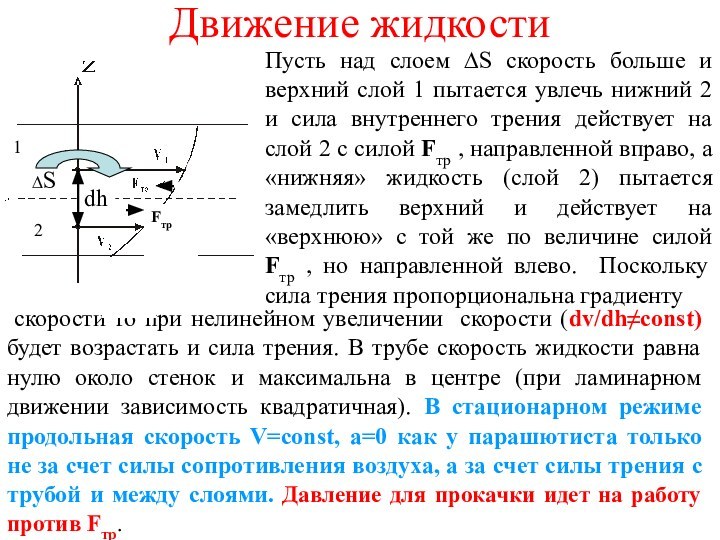
Движение жидкости
Пусть над слоем ∆S скорость больше и
верхний слой 1 пытается увлечь нижний 2 и сила
внутреннего трения действует на слой 2 с силой Fтр , направленной вправо, а «нижняя» жидкость (слой 2) пытается замедлить верхний и действует на «верхнюю» с той же по величине силой Fтр , но направленной влево. Поскольку сила трения пропорциональна градиенту
скорости то при нелинейном увеличении скорости (dv/dh≠const) будет возрастать и сила трения. В трубе скорость жидкости равна нулю около стенок и максимальна в центре (при ламинарном движении зависимость квадратичная). В стационарном режиме продольная скорость V=const, а=0 как у парашютиста только не за счет силы сопротивления воздуха, а за счет силы трения с трубой и между слоями. Давление для прокачки идет на работу против Fтр.
dh
∆S
Fтр
2
1
Слайд 3
Единицы измерения и Формула Пуазейля
Единицей вязкости в
системе единиц СИ является паскаль-секунда (Па с=Н с/м2). Как
следует из формулы на 1 слайде, это такая вязкость, при которой градиент скорости с модулем, равным 1 м/с на высоте 1м, приводит к возникновению силы внутреннего трения в 1Н на 1м2 поверхности касания слоев. Г.Хаген в 1839, повторно Пуазейль в 1840-41 рассчитали поток вязкой несжимаемой жидкости ламинарно протекающей через поперечное сечение тонкой цилиндрической трубки в единицу времени
Основной вклад дает диметр трубы d4 (вулканы) а не разность давления р1-р2 и длина l. Связь k и установлена Стоксом в 1845. Понятие вязкости относится и к реальным газам!
Слайд 4
Ламинарное и турбулентное течения.
Ламинарным называется такое течение жидкости,
когда отдельные слои жидкости двигаются друг относительно друга не
перемешиваясь. На всей длине потока частицы жидкости не переходят из одного слоя в другой. Слово «ламинарное» происходит от латинского «lamina», что означает пластинку, полоску. На самом деле так как есть силы трения, то и определенное перемешивание есть всегда. Если оно мало то будем условно называть ламинарное.
Ламинарное течение стационарно!
Если направление скорости частиц жидкости в каждой точке пространства постоянно изменяется (не важно беспорядочно или периодически), то такое течение называется турбулентным.
Турбулентное течение нестационарно!
Слайд 5
Число Рейнольдса
Один тип движения может переходить в другой,
например, просто при изменении скорости течения. Влияют на этот
переход и другие параметры. Английский физик Рейнольдс установил, что характер движения зависит от безразмерной величины:
где ρ – плотность жидкости, v - средняя по сечению трубы скорость потока, η – вязкость жидкости, l – усредненный характерный для поперечного сечения потока размер (для трубы диаметр). Величина Re называется числом Рейнольдса. Проще: критерий подобия для течения вязких жидкостей и газов. Чем больше вязкость тем Re меньше! Это не константа для данной жидкости! Зависит от условий температуры, размера и т.д.
Слайд 6
Значения числа Рейнольдса.
При малых значениях Re наблюдается ламинарное
течение, а начиная с некоторого значения Re, называемого критическим,
течение становится турбулентным. Например, если в качестве характерного размера круглой трубы взять ее радиус, то критическое значение числа Рейнольдса для течения воды получается равным примерно 1150 (если за характерный размер выбрать диаметр, то критическое значение будет примерно 2300). Может достигать 17? миллионов и более (важно для теплообмена)!
Введение числа Рейнольдса необходимо при моделировании: характер течения жидкостей, например, в трубах разных сечений будет одинаков, если каждому течению соответствует одно и то же число Рейнольдса.
В 2009 году профессор Peter Egolf точно решил задачу перехода от ламинарного течения к турбулентному. Процесс носит критический характер. Можно провести аналог с точкой Кюри в магнетиках (Т/Тс)!
Слайд 7
Факультативно : Питер Егольф показал, что
поведения турбулентности
в жидкости по характеру
близко к критическим явлениям в
магнетизме
1 http://commons.wikipedia.org/wiki/Image:Weiss-Bezirke2.png
2 Als-Nielsen J., Dietrich O.W., Passell L., Phys. Rev. 14, 4908, 1976.
3 http://www-chaos.umd.edu/gallery/pattern.html, Nam K., Ott E., Antonsen Jr. Th.,
Guzdar P.N., Phys. Rev. Lett. 84, 5134, 2000.
4 Egolf P.W., A statistical theory of turbulence, submitted to the Int. J. Refr., 2009.
5 Zagarola M.V., Perry A.E., Smits A.J., Phys. Fluids 9 (7), 2094, 1997.
Слайд 8
Число Рейнольдса в природе
Число Re определяет характер не
только течения жидкостей и не только в жестких конструкциях
(типа труб), но и в реках и в живых организмах. Оно может характеризовать движение машин на дорогах (аварии или перестроения из полосы в полосу аналог внутреннего трения или турбулентности). Течение крови в кровеносной системе происходит полностью в соответствии с законами гидродинамики. Однако уменьшение l (сужение сосуда – тромб, бляшка, передавливание ) ведет к изменению Re и следовательно характера движения крови (турбулентности). Мышцами сердца кровь выталкивается в аорту и далее в артерии, артериолы, капилляры и вены. В такой же последовательности наблюдается и падение давления. Течение крови обычно имеет ламинарный характер. Но при возрастании скорости течения (например, в периоды напряженной деятельности человека) оно может стать и турбулентным. Изменение характера течения крови легко можно услышать с помощью медицинского стетоскопа.
Слайд 9
Кровяное давление
У человека измеряются два давления: максимальное в
момент выталкивания крови в аорту (систолическое около 120 мм
рт.ст. ~0.16 атм.), и минимальное, устанавливающееся между сокращениями сердца (диастолическое около 80 мм рт.ст.~0.08атм.) . 1 атм.=760 мм.рт.ст.
Для измерения давления искусственно вызывают переход течения крови от ламинарного к турбулентному. Обычно на плечевой артерии или на запястье накачивают эластичную ленту воздухом до остановки течения крови и затем потихоньку уменьшают давление. Звук появляется когда давление в ленте падает ниже систолического и кровь начинает бурное протекание. Звук турбулентного течения пропадает, когда давление в ленте уже не обеспечивает сжатие артерии и течение становится ламинарным (диастолическое давление).
Характер протекания воздуха при вдыхании (храп), обтекание воздухом ГЗ, поток машин и т.д. тоже можно охарактеризовать числом Рейнольдса.
Слайд 10
Факультативно: Геодинамо и магнитные полюса
На фото: Виртуальная
частица в жидком железе внешнего ядра Земли стремится передвигаться
к поясам планеты когда условия геодинамо меняются. Цвет характеризуют турбулентное движение : красным цветом показано положительное течение (с востока на запад), а синим – отрицательное (с запада на восток). Слева направо - так течение меняется с ростом чисел Рэлея, которые отражают неустойчивость жидкости и образование конвекции. Сверху вниз – так поток реагирует на увеличение угловых скоростей всей системы геодинамо.
Слайд 11
Японские ученые предсказывают существование в земном ядре зональных

течений. Примеры зональных течений на Земле -потоки ветра, которые
циркулируют вокруг земного шара или Гольфстрим. Аналоги могут существовать и в турбулентном расплавленном ядре. Магнитные полюса планеты образуются из-за конвекции расплавленного железа внутри планеты.
Была смоделирована работа геодинамо при небольших вязкостях, чтобы построить картину конвекции во внешних слоях земного ядра. Численная модель подтверждает, что обнаруженная двойная конвекционная структура может сосуществовать с главной конвекцией, которая приводит к образованию магнитных полюсов у планеты. Дополнительные конвекционные течения это радиальные плюмы – течения из внутреннего ядра и зональное течение, направленное с востока на запад . Новый тип зонального течения может объяснить механизм переключения полюсов. В последний раз северный и южный полюс поменялись местами около 780 000 лет назад и стоит ожидать следующий «щелчок». «Переключении полюсов» в реальности длится около 10 000 лет.
Zonal flow formation in the Earth’s core. Takehiro Miyagoshi, Akira Kageyama & Tetsuya Sato. Nature 463, 793-796 (11 February 2010) | doi:10.1038/nature08754.
http://physicsworld.com/cws/article/news/41686
Слайд 12
Физика дождя
Почему капля не летит с ускорением свободного
падения и не пробивает дырку в шляпе или машине?
Маленький парашют? Бронемашина с парашютами приземляется со скоростью 7-8 м/c!
Капля хороший пример. Как оказалось на полет влияет и сила тяжести, и сила трения, и сила поверхностного натяжения и даже упругий удар! Как говорили на прошлой лекции на рост размера может влиять даже статический заряд
Слайд 13
Теоретическая физика …..дождя
Когда водяной пар конденсируется, то
в облаках образуются капли диаметром от 10-20 мкм –
меньше человеческого волоса. Они слишком маленькие, чтобы выпасть в виде дождя, Падение начинается при размере 55 мкм и более. На скорость капли влияют ее вес, жидкое трение и сопротивление воздуха. Если капли крошечные, как те, из которых состоят облака, сопротивление среды определяется только силами трения и число Рейнольдса настолько маленькое, что можно применить формулу Стокса (см. лекцию 4): сопротивление воздуха пропорционально вязкости, радиусу капли и ее скорости Fтр = -bv= - 6πηRv. Для обычной облачной капли с радиусом 0.01 мм получится скорость около 1 см/c. Это слишком мало. Но она быстро растет с размером: так как вес капли пропорционален радиусу в кубе, а сопротивление просто радиусу, то скорость будет расти пропорционально квадрату ее радиуса. Эти выкладки справедливы для сферической капли до d=0.1 мм.
Слайд 14
Теоретическая физика… дождя
По мере роста размера капли позади
нее возникают завихрения и возникает пониженное давление и следовательно
дополнительный вклад в сопротивление влажного воздуха за счет разности давлений. Для обычных дождевых капель (более 1 мм) необходимо учитывать силы турбулентности. Модуль скорости определяется балансом между весом капли и силой сопротивления воздуха:
То есть сила сопротивления пропорциональна площади капли, коэффициенту сопротивления C, равному 0.5 для сферы при существенных числах Рейнольдса, скорости и плотности воздуха ρ.
Т.е. начинает появляться парусность! Фактически все тоже что и на 4 лекции когда мы изучали жидкое трение просто b1=0.25ρS. Можно показать, что капля в 1 мм разовьет скорость 16 км в час (4.4 м/с). Можно , было бы даже предположить , что капля в 5 мм разгонится до 35 км в час (9.7 м/с)……но………
Слайд 15
Физика дождя
Сто лет назад немецкий физик Филипп Леонард
заметил, что если диаметр капли превышает 3 мм, то
она деформируется и превращается в нечто, напоминающее блин. Поэтому ее площадь становится больше, чем у сферической капли такой же массы. Значит, растет сопротивление, но больше не увеличивается скорость. И для капель с диаметром 3-4 мм, скорость выходит на асимптотическое значение около 29 км в час (или 8 м/c, опять парашют). При 5.5 мм силы настолько вырастают, что сила поверхностного натяжения больше не в состоянии удерживать воду в форме капли, и она рассыпается. Капли, диаметр которых превышает 5 мм, не живут! Но водной капли молекул больше, чем звезд на небе!
Слайд 16
Опять парашют?
Совсем недавно исследователям удалось объяснить возникновение быстрых
дождевых капель.
Для падающей капли с некоторого момента сила сопротивления воздуха уравнивает силу притяжения Земли и скорость капли прекращает расти. Таким образом, свободно падающая капля фиксированного размера может, как мы уже знаем, разогнаться только до определенной скорости, которую называют предельной. Выяснилось, что капли, скорость которых выше предельной, образуются в результате разрушения более больших и быстрых капель.
Слайд 17
Дождевые капли сильно отличаются по размерам: диаметр большинства
- менее одного миллиметра, однако некоторые достигают в размере
пяти миллиметров.
Можно предположить, что в облаках капли образуются примерно одинакового размера. При падении они сталкиваются и происходит разброс по размерам? Не совсем! Установлено, что во время самого сильного дождя на кубический метр приходится не более тысячи капель. Это мало для интенсивного столкновения (но какие то столкновения точно есть. См. далее).
Ученые засняли падение капли на видео и показали, что сопротивление воздуха приводит к деформации капли (она как мы и говорили она становится похожей на блин или парашют) и разрушается. Теоретические расчеты подтвердили обнаруженное распределение капель по размерам .
Но все не так просто…….
Сталкиваются капли дождя?
Слайд 18
В 2009 году ученые нашли сверхбыстрые дождевые капли
Как
мы у же знаем для падающей капли с некоторого
момента сила сопротивления воздуха уравнивает силу притяжения Земли и скорость капли больше не возрастает (ускорения нет). Свободно падающая капля фиксированного размера может разогнаться только до определенной скорости, которую называют предельной. Например, для капли диаметром 100 мкм предельная скорость равна 0.30 м/c.
Ученые в Мехико в безветренную погоду наблюдали за падением более 64 тысяч капель . Обнаружено, что капли движутся с существенно более высокими скоростями, чем мы уже обсуждали и большое количество капель летит быстрее скорости, характерной для их размера.
Слайд 19
Установлено, что много мелких капель движется
со скоростями, превосходящими расчетный предел. Т.е. капли размером 100
мкм оказались способны падать со скоростью 3-4 м/с (в 10 раз быстрее чем мы оценили ранее). Это может являться результатом того, что все капли разного размера и следовательно падают вертикально с разной скоростью и сталкиваются (в том числе часть разрушаются).
После столкновения капли движутся со скоростью исходных объектов (вспомним закон сохранения импульса и опыт с шарами), для которых предельное значение скорости могло быть значительно выше. Удалось установить, что с увеличением силы дождя растет и относительное количество мелких сверхбыстрых капель. Результаты найдут применение при создании компьютерных моделей климатических изменений.
На мой взгляд работают оба механизма. Т.е когда дождь не очень интенсивный капли не сталкиваются и работает «парашют», а если интенсивный то начинаются столкновения.
Слайд 20
Факультативно: Не только студенты любят весенний дождичек или
законы жидкого кратерообразования
От чего зависит
форма кратера от падения капли? Меняются ли капли сами и изменяют ли они форму поверхности, на которую они падают? Исследователи капали на поверхность, покрытую кремниевыми гранулами каплями диаметром 4-50 мкм с высоты 10-480 мм и выяснили, что самые маленькие кратеры создаются на средних скоростях, а самые глубокие кратеры – на максимальных. При высоких скоростях в центре кратера оставался холмик, а не выемка. При этом капли большего размера оставляли более мелкие кратеры.
Установлено, что на радиус кратера влияет не только отношение плотности поверхности (гранул) и плотности падающей жидкости, но и отношение инерции жидкости к поверхностному натяжению.
энергию из воздуха?
Аналогично механизму образования зарядов в грозовых облаках
ученые предлагают добывать энергию из воздуха. Идею получения электричества из атмосферы выдвигал еще Тесла. Как мы уже знаем жидкая вода присутствуют в облаках в виде аэрозоля. При взаимодействии микрочастиц происходит разделение зарядов. Далее идет физическое расслоение системы частиц (тяжелые располагаются внизу облака), а следовательно и разделение зарядов. При определенном напряжении происходит пробой.
В условиях высокой влажности воздуха ученые наблюдали, как контактируют микрочастицы воды и кремния и фосфата алюминия. В результате микрочастицы кремний имели отрицательный заряд, а алюминия — положительный. Т.е. вода в атмосфере способна накапливать электрический заряд и передавать его материалам, с которыми она контактирует.
Слайд 22
Краевой угол
Если жидкость находится на твердой поверхности, то
ее форма зависит от соотношения трех сил:
силы тяжести, сил
взаимодействия между молекулами жидкости (силами натяжения) и сил взаимодействия с молекул жидкости с молекулами твердого тела (две последние силы Ван-дер-Ваальса). Характерным параметром в этом случае является краевой угол , то есть угол, образованный касательной к поверхности жидкости у ее границы с твердым телом и поверхностью твердого тела. В данной точке соприкасаются три фазы: газ, жидкость и твердое тело и существуют три силы натяжения. Привычная нам сила на границе воздух-жидкость, а так же силы натяжения на границах твердое тело –газ и жидкость твердое тело. Угол определяется балансом этих трех сил натяжения.
твердая поверхность
жидкость
газ
Слайд 23
Явления смачивания и несмачивания
При =0 имеем
полное растекание жидкости, называемое полным смачиванием. Например, вода на
чистом стекле (поверхности жидкости тела параллельны).
При =π наблюдаем полное несмачивание твердого тела жидкостью. Например, вода на парафине.
Случай <π/2 называют частичным смачиванием
При >π/2 имеем частичное несмачивание.
твердая поверхность
жидкость
газ
Слайд 24
Давление под искривленной поверхностью жидкости
поверхности к сокращению
за счет сил натяжения, а под вогнутой поверхностью по
этим же причинам несколько растянут. Величина дополнительного давления зависит от двух параметров – поверхностного натяжения σ и кривизны поверхности R. Для сферической поверхности c радиусом R:
Объем жидкости под выпуклой поверхностью всегда несколько сжат за счет стремления
Слайд 25
Средняя кривизна
Для произвольной кривой поверхности (типа седла)
введем понятие средней кривизны: в интересующей нас точке проводится
нормаль к поверхности и через нее проводятся две взаимно перпендикулярные плоскости, в каждой из которых получим линию пересечения с поверхностью с различным, в общем случае, радиусом кривизны. Такие сечения называются нормальными. Величину Rсред равную полусумме обратных радиусов и называют средней кривизной поверхности в данной точке:
Лаплас доказал, что в общем случае для поверхности произвольной формы дополнительное давление равно:
формула Лапласа.
Слайд 26
Капиллярные явления
Если дистанция между поверхностями произвольной формы,
ограничивающими движение жидкости, сравнима с радиусом кривизны поверхности данной
жидкости, то такие объекты называются капиллярами. Особенности поведения жидкости в таких объектах (например, тонких трубках) и называют капиллярными явлениями. В зависимости от величины сил Ван-дер-
Ваальса (силы взаимодействия жидкости и поверхности или проще смачиваемости жидкости) форма поверхности может быть как вогнутой так и выпуклой. Такие поверхности получили название мениск. Одно из характерных капиллярных явлений
– подъем жидкости в капилляре, если он помещен в смачивающую жидкость и опускание уровня, если она несмачивающая (из-за Δp).
Слайд 27
Капиллярные явления
В случае сферической поверхности жидкости с радиусом
кривизны R уровень жидкости в капилляре будет изменяться до
тех пор, пока давление Лапласа не уравновесится гидростатическим давлением столба жидкости ρgh (ρ – плотность жидкости):
Если учесть краевой угол и радиус капилляра r, то как видим на рисунке r=Rcos, получаем высоту подъема в зависимости от радиуса капилляра:
h