(Å-1)
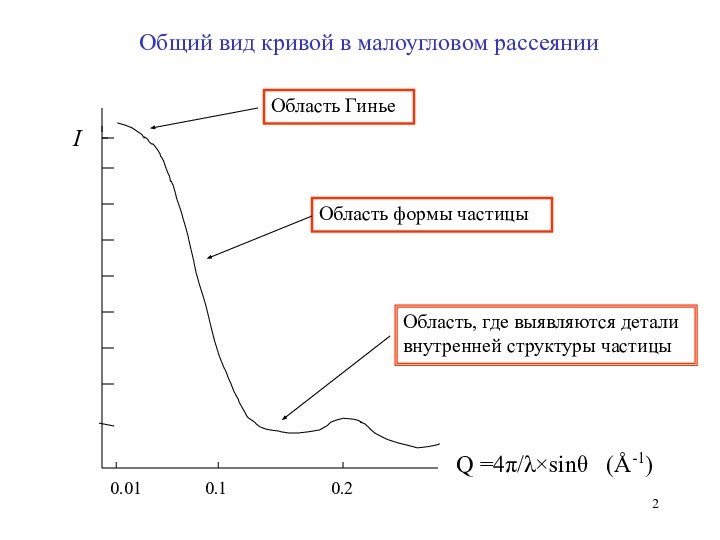
Область Гинье
Область формы частицы
Область, где выявляются детали внутренней структуры
частицы 0.01 0.1 0.2
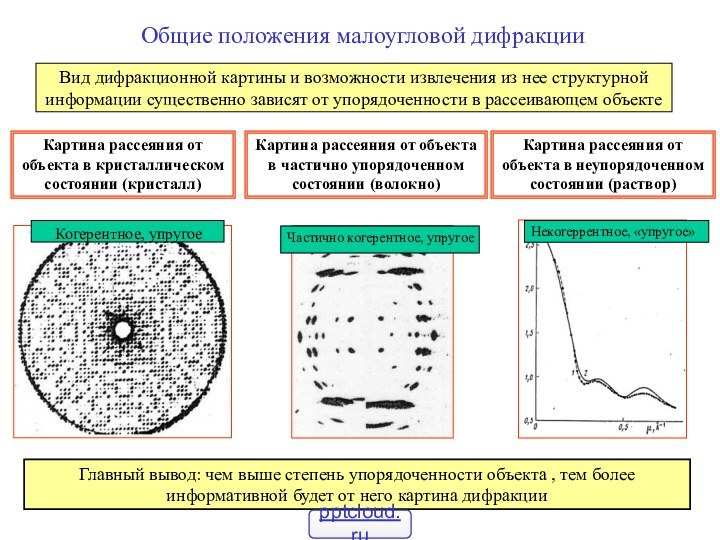
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть







0.01 0.1 0.2
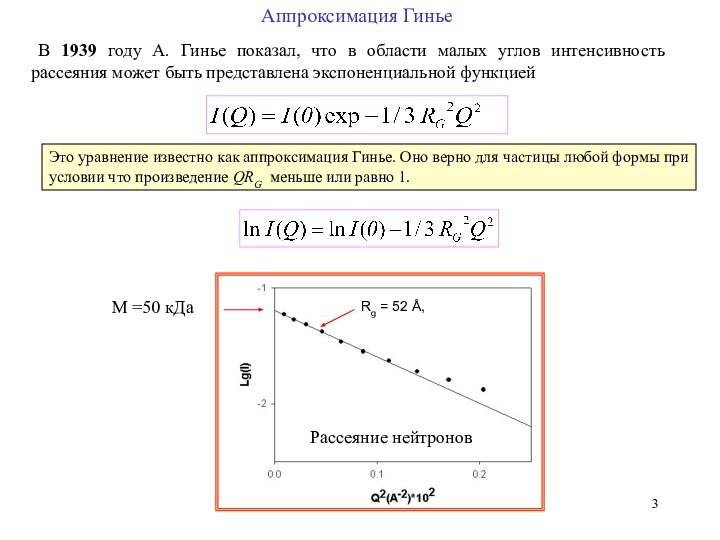
Аппроксимация Гинье
Это уравнение известно как аппроксимация Гинье. Оно верно для частицы любой формы при условии что произведение QRG меньше или равно 1.
Rg = 52 Å,
M =50 кДа
Рассеяние нейтронов
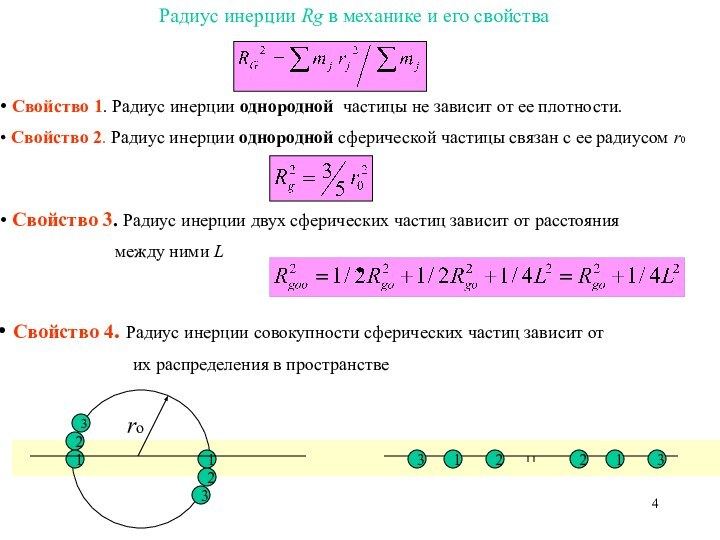
Свойство 3. Радиус инерции двух сферических частиц зависит от расстояния
между ними L
Свойство 4. Радиус инерции совокупности сферических частиц зависит от
их распределения в пространстве
1
2
3
1
2
3
3
1
2
2
1
3
ro
2
1
2
2
2
1
1
1
Rg Rg Rg Rg
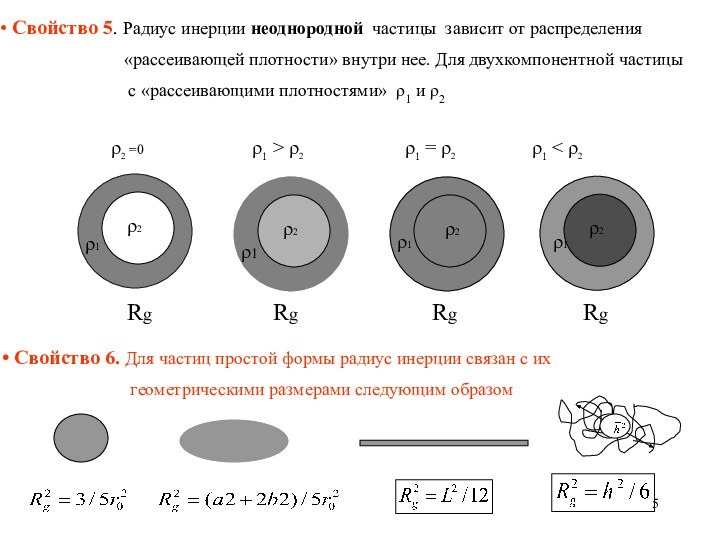
2 =0 1 > 2 1 = 2 1 < 2
Свойство 6. Для частиц простой формы радиус инерции связан с их
геометрическими размерами следующим образом
2
1
2
2
2
1
1
1
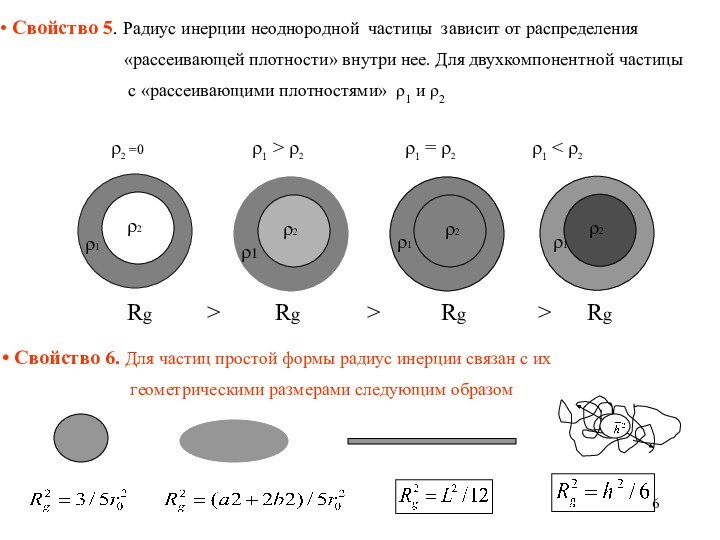
Rg > Rg > Rg > Rg
2 =0 1 > 2 1 = 2 1 < 2
Свойство 6. Для частиц простой формы радиус инерции связан с их
геометрическими размерами следующим образом
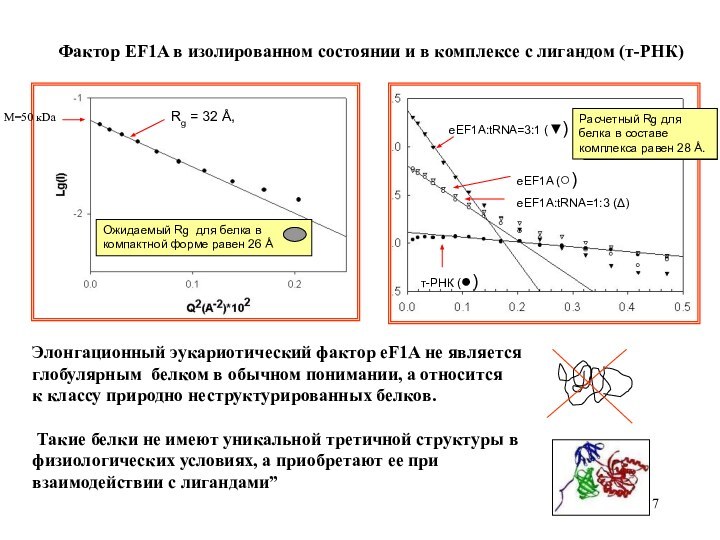
т-РНК (●)
eEF1A:tRNA=3:1 (▼)
eEF1A (○)
eEF1A:tRNA=1:3 (Δ)
Расчетный Rg для белка в составе комплекса равен 28 Å.
Элонгационный эукариотический фактор eF1A не являeтся
глобулярным белком в обычном понимании, а относится
к классу природно неструктурированных белков.
Такие белки не имеют уникальной третичной структуры в физиологических условиях, а приобретают ее при
взаимодействии с лигандами”
М=50 кDa
Фактор EF1A в изолированном состоянии и в комплексе с лигандом (т-РНК)
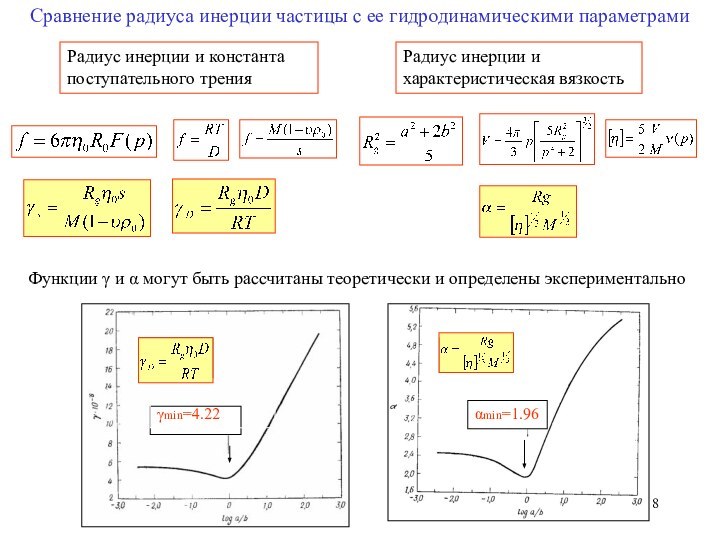
γmin=4.22
αmin=1.96
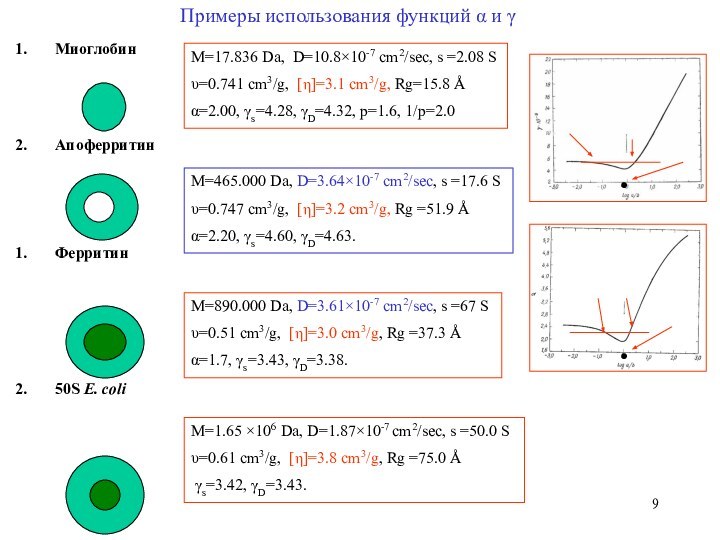
M=465.000 Da, D=3.6410-7 cm2/sec, s =17.6 S
=0.747 cm3/g, []=3.2 cm3/g, Rg =51.9 Å
=2.20, s=4.60, D=4.63.
M=890.000 Da, D=3.6110-7 cm2/sec, s =67 S
=0.51 cm3/g, []=3.0 cm3/g, Rg =37.3 Å
=1.7, s=3.43, D=3.38.
M=1.65 106 Da, D=1.8710-7 cm2/sec, s =50.0 S
=0.61 cm3/g, []=3.8 cm3/g, Rg =75.0 Å
s=3.42, D=3.43.
•
•
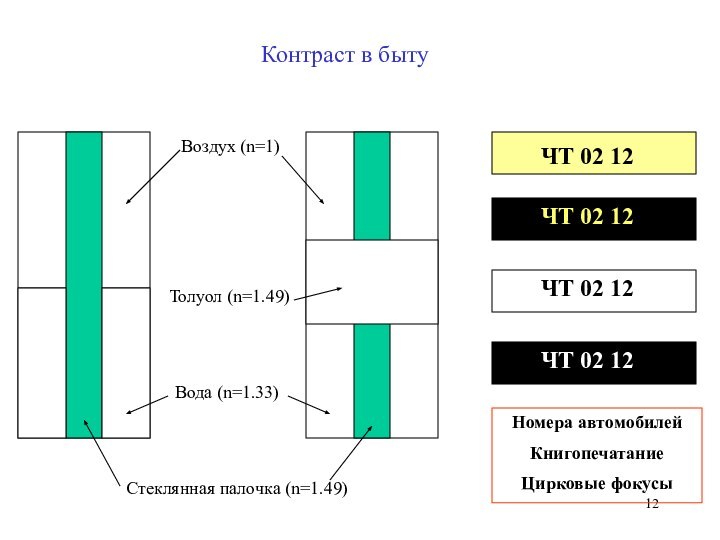
ЧТ 02 12
Номера автомобилей
Книгопечатание
Цирковые фокусы
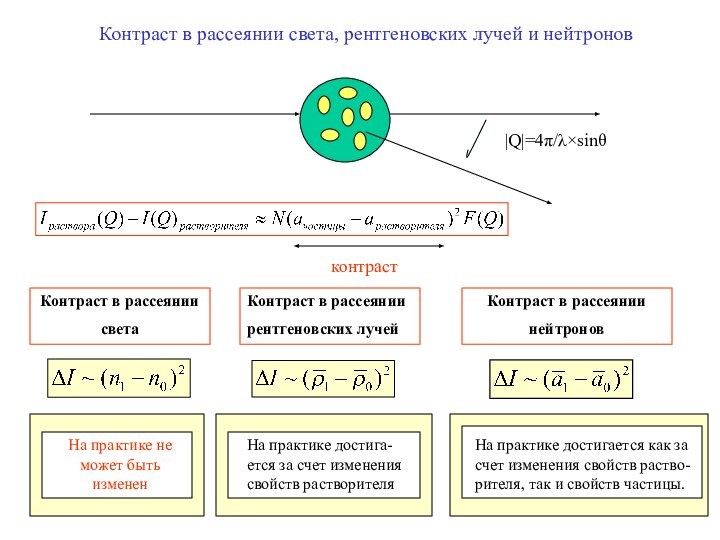
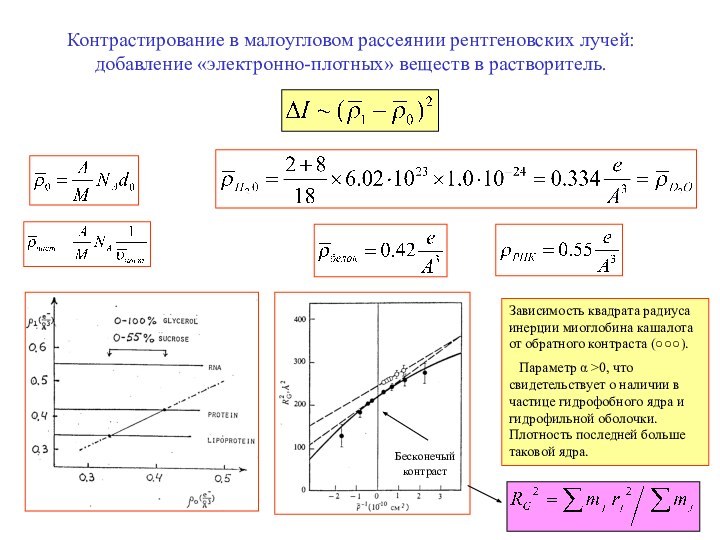
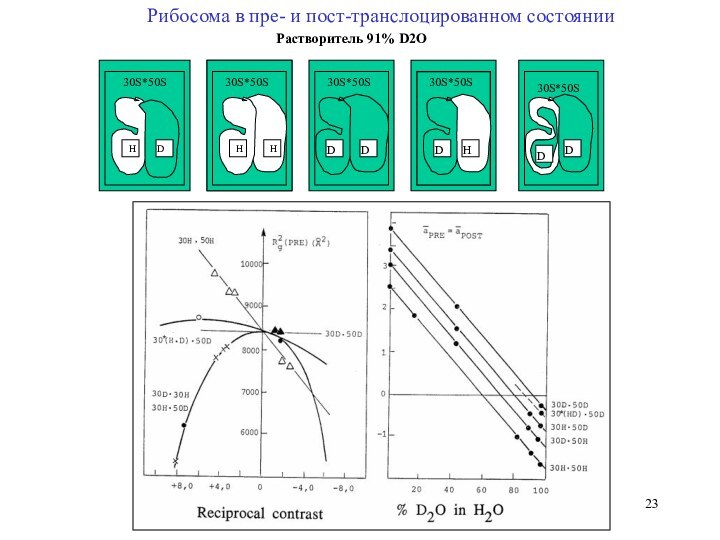
Контраст в рассеянии
нейтронов
На практике не может быть изменен
На практике достига- ется за счет изменения свойств растворителя
На практике достигается как за счет изменения свойств раство- рителя, так и свойств частицы.
|Q|=4/sin
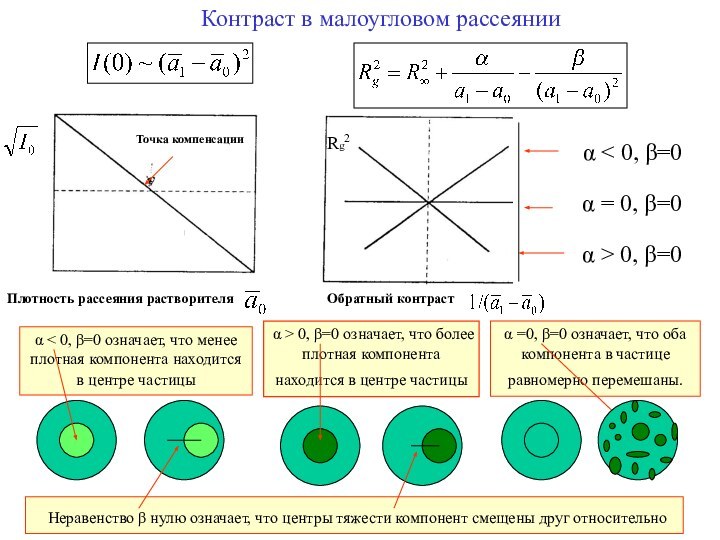
Бесконечый контраст
α < 0, β=0 означает, что менее плотная компонента находится в центре частицы
α > 0, β=0 означает, что более плотная компонента находится в центре частицы
α =0, β=0 означает, что оба компонента в частице равномерно перемешаны.
Неравенство β нулю означает, что центры тяжести компонент смещены друг относительно
aH = -3.7410-13 aD = +6.69 10-13
aN = +9.4010-13 aO = +5.80 10-13
aP = +5.1110-13 aC = +6.05 10-13
При бесконечном отрицательном или положительном контрасте проявляется форма частицы
При малом контрасте проявляется внутренняя структура
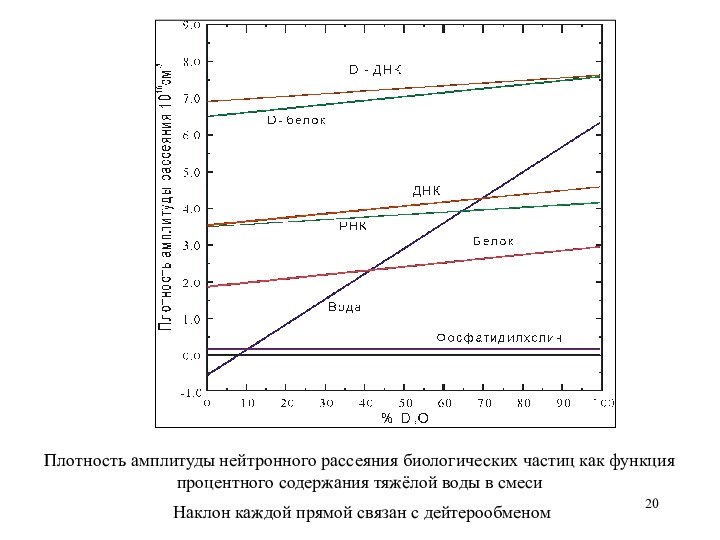
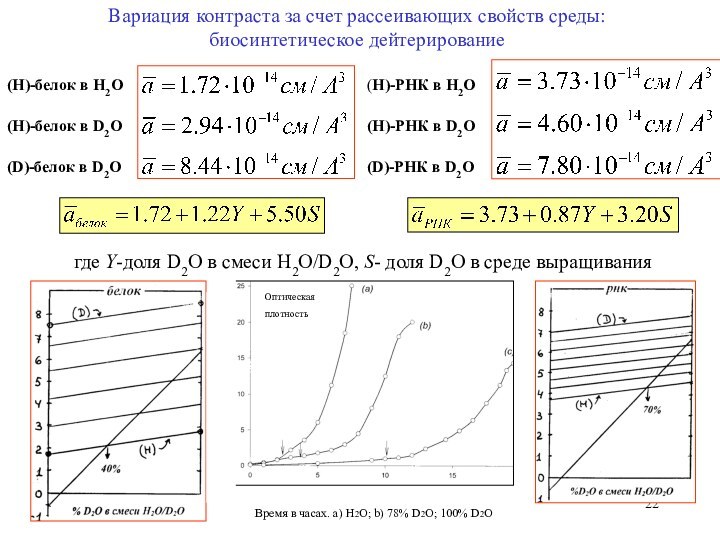
где Y-доля D2O в смеси H2O/D2O, S- доля D2O в среде выращивания
Оптическая
плотность
Время в часах. a) H2O; b) 78% D2O; 100% D2O
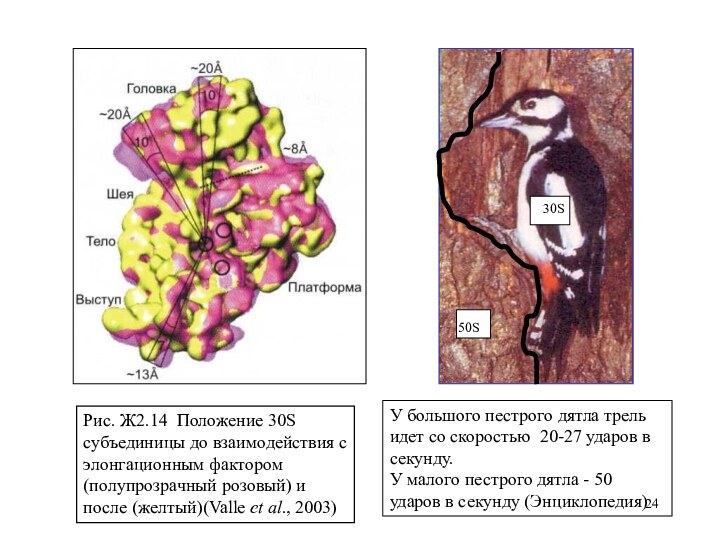
У большого пестрого дятла трель идет со скоростью 20-27 ударов в секунду.
У малого пестрого дятла - 50 ударов в секунду (Энциклопедия)
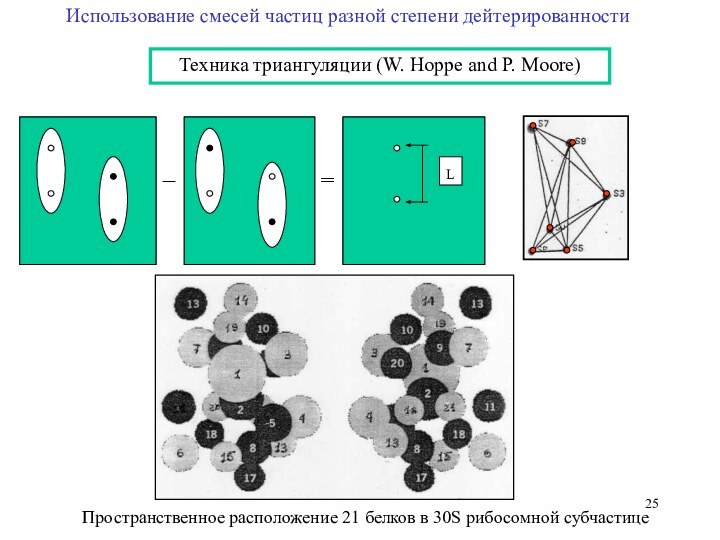
L
_
=
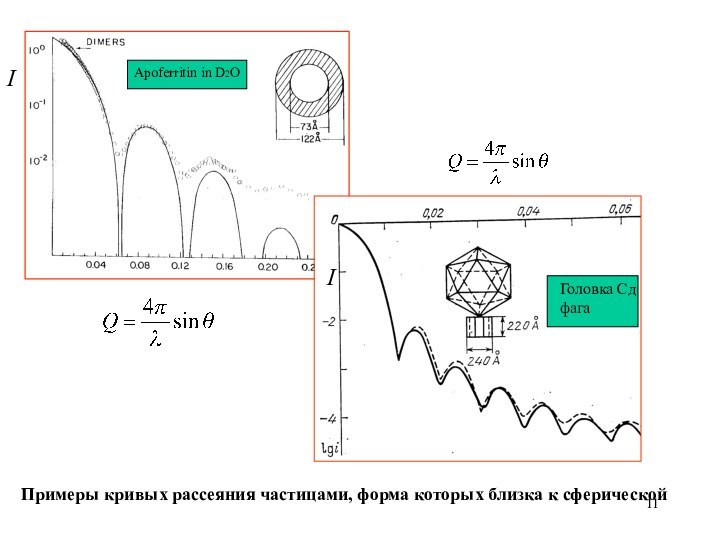
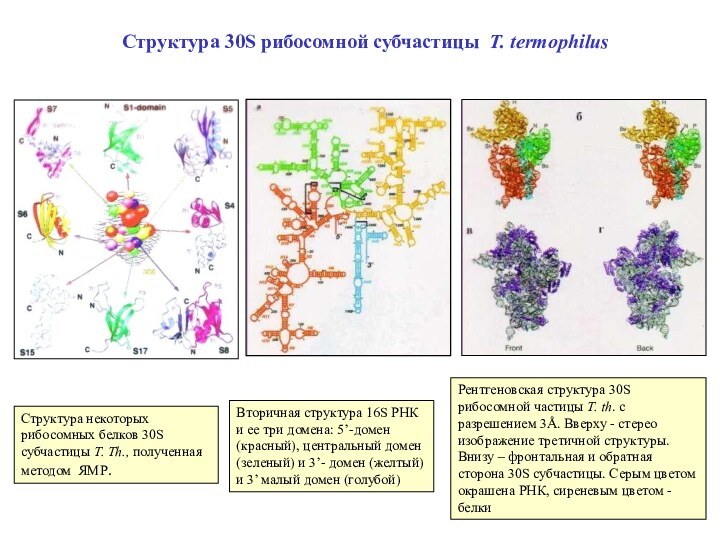
Структура 30S рибосомной субчастицы Т. termophilus
Вторичная структура 16S РНК и ее три домена: 5’-домен (красный), центральный домен (зеленый) и 3’- домен (желтый) и 3’ малый домен (голубой)
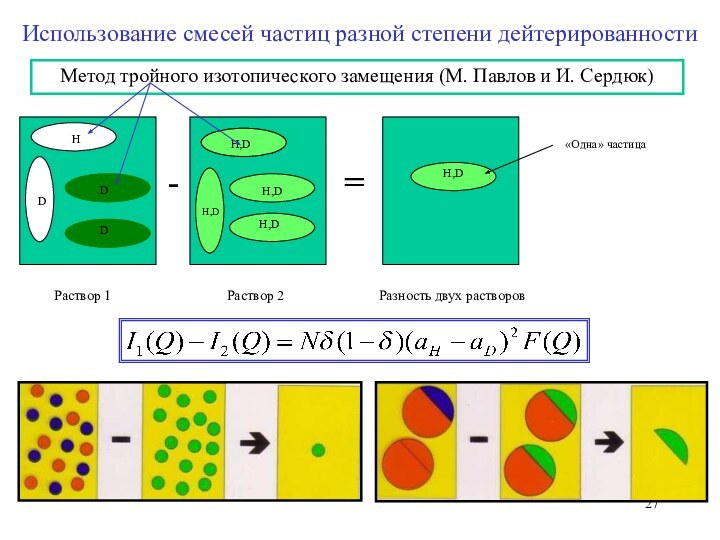
«Одна» частица