Слайд 2
Цель учебная:
Сформировать
у студентов понятие «гармоническое колебание» и научить определять параметры
колебаний математическими способами.
Задачи урока:
1. Показать аналогию между параметрами, характеризующими механические и электромагнитные колебания.
2. Раскрыть сущность определения параметров по уравнениям гармонических колебаний и их графикам.
3. Раскрыть принцип построения графиков гармонических колебаний по их уравнениям.
Развивающая цель:
Показать студентам роль межпредметных связей при изучении курсов математики и физики; раскрыть сущность аналогии как метода научного познания.
Воспитательная цель:
Воспитания устойчивого интереса студентов к достижению результатов своей работы.
Слайд 3
Формы и методы обучения
беседа;
рассказ;
объяснительно-иллюстрационный:
проблемные ситуации:
метод суждения.
Слайд 4
Структура занятия:
Актуализация знаний.
Мотивация учебной деятельности.
Постановка цели.
Формирование новых знаний.
Контроль
полученных знаний.
Подведение итогов.
Домашнее задание.
Слайд 5
Актуализация раннее усвоенных знаний.
Преподаватель физики задает вопросы студентам:
Что
собой представляют колебания?
В каких разделах физики мы о них
говорили? Приведите примеры.
Студенты отвечают на поставленные вопросы
Слайд 6
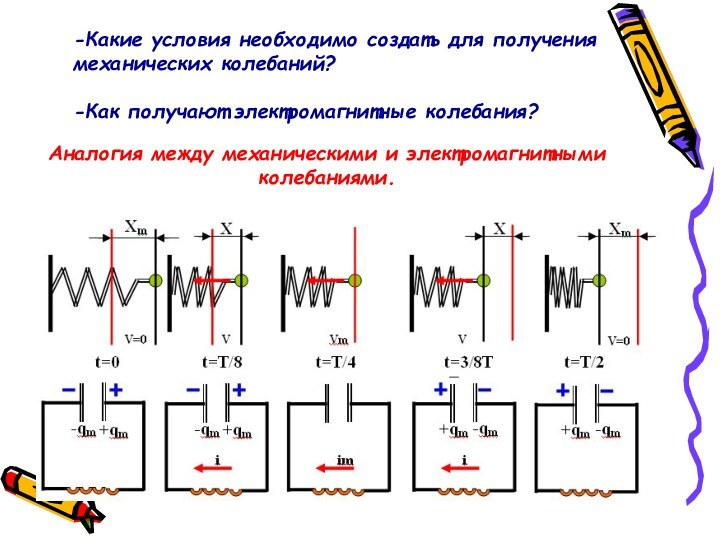
Аналогия между механическими и электромагнитными колебаниями.
-Какие условия необходимо
создать для получения механических колебаний?
-Как получают электромагнитные колебания?
Слайд 7
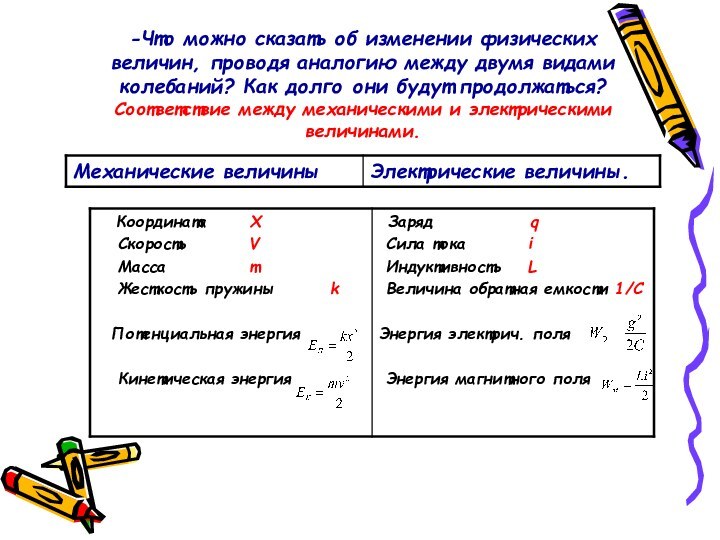
-Что можно сказать об изменении физических величин, проводя
аналогию между двумя видами колебаний? Как долго они будут
продолжаться?
Соответствие между механическими и электрическими величинами.
Слайд 8
Мотивация учебной деятельности
Преподаватель физики отмечает, что колебания свойственны
всем явлениям природы: пульсируют звезды, вращаются планеты, внутри организма
бьется сердце и т. д. Вам известна природа возникновения механических и электромагнитных колебаний.
Вопрос: Как вы думаете, какими же параметрами будут характеризоваться рассмотренные нами колебательные процессы?
(Студенты правильного ответа на вопрос не дают, т.к. у них не хватает знаний)
Слайд 9
Постановка цели урока
Правильно ответить на поставленный вопрос вам
поможет изучение явлений «гармонические колебания в физике». Изучение данного
явления невозможно без знаний, полученных из курса математики. Сегодня вам предстоит познакомиться:
во –первых, с основными понятиями и терминами теории колебания;
во–вторых, с математическими соотношениями, описывающими колебания.
И первое, и второе очень важно для понимания всего последующего курса физики.
Слайд 10
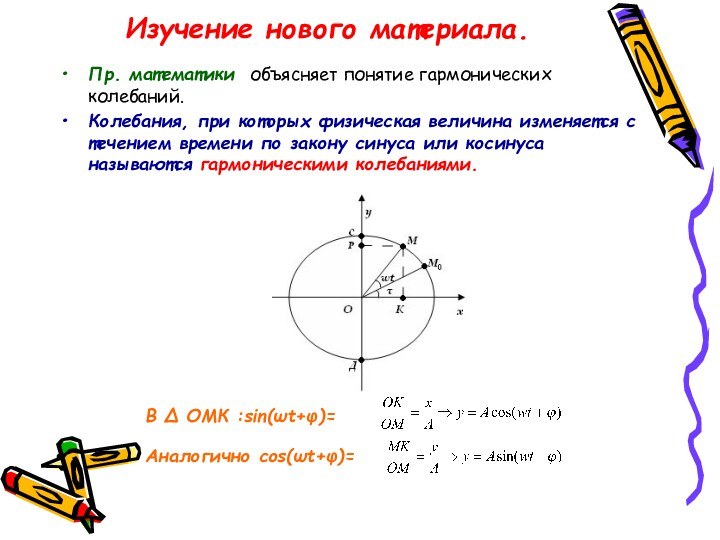
Изучение нового материала.
Пр. математики объясняет понятие гармонических колебаний.
Колебания,
при которых физическая величина изменяется с течением времени по
закону синуса или косинуса называются гармоническими колебаниями.
В ∆ ОМК :sin(ωt+φ)=
Аналогично cos(ωt+φ)=
Слайд 11
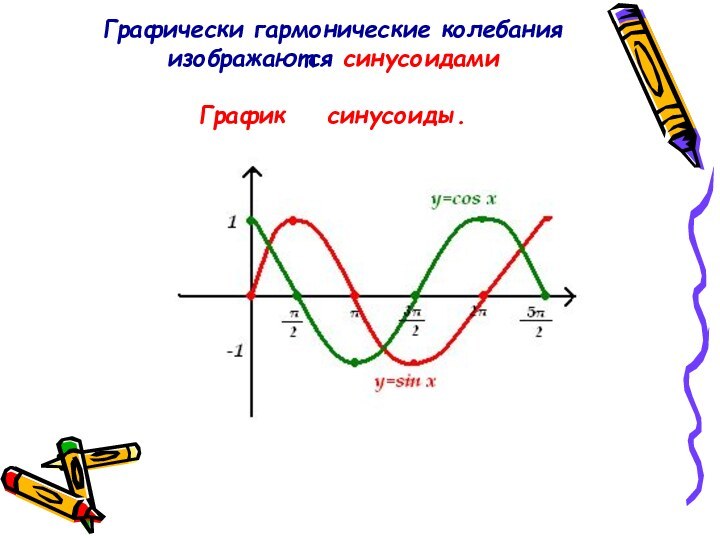
Графически гармонические колебания изображаются синусоидами
График синусоиды.
Слайд 12
Пр. физики предлагает студентам объяснить :
«Почему колебания
груза на пружине и свободные колебания в закрытом контуре
можно представить с помощью гармонического закона косинуса?»
Слайд 13
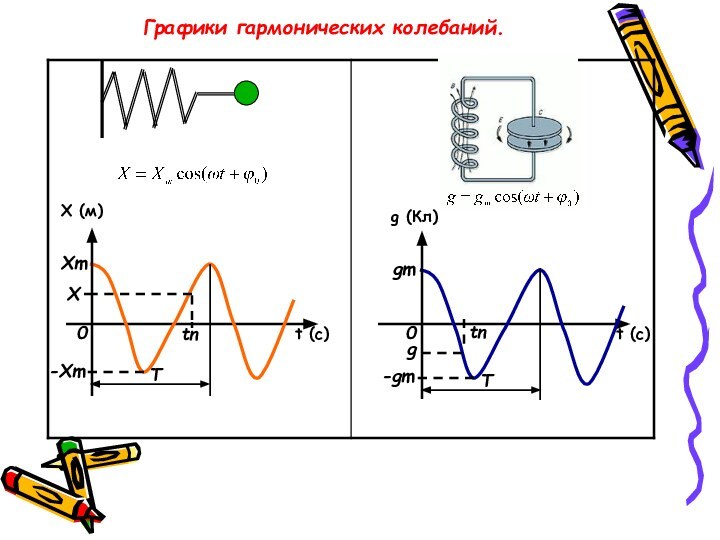
Графики гармонических колебаний.
Х (м)
t (c)
g (Кл)
t (c)
Хm
-Хm
0
0
tn
Х
tn
gm
-gm
g
Т
Т
Слайд 14
Пр. математики, используя уравнения гармонических колебаний и их
графики, вводит понятие гармонических колебаний.
, Параметры гармонических колебаний.
1. Модуль
наибольшего значения колеблющейся величины называется амплитудным значением.
Хm(м) – амплитуда механического колебания;
gm(Кл) – амплитуда заряда конденсатора;
Im(A) – амплитуда силы тока;
Um(B) – амплитуда напряжения .
2. Значение колеблющейся величины в любой момент времени называется мгновенным значением.
Хm(м) – амплитуда механического колебания;
gm(Кл) – амплитуда заряда конденсатора;
Im(A) – амплитуда силы тока;
Um(B) – амплитуда напряжения
Слайд 15
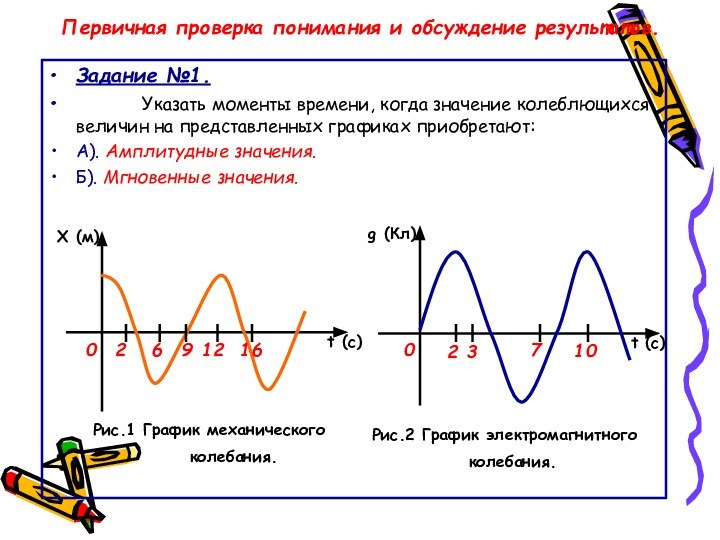
Первичная проверка понимания и обсуждение результатов.
Задание №1.
Указать моменты времени, когда значение колеблющихся величин
на представленных графиках приобретают:
А). Амплитудные значения.
Б). Мгновенные значения.
Х (м)
t (c)
t (c)
0
0
g (Кл)
Рис.1 График механического
колебания.
Рис.2 График электромагнитного
колебания.
2
6
9
12
16
2
3
7
10
Слайд 16
Изучение нового материала.
Параметры гармонических колебаний.
Пр. математики:
3. Минимальный промежуток
времени, в течении которого значение колеблющейся величины полностью повторяется
называется периодом колебания.
Т (с) – период колебания.
Пр. физики :
Период собственных незатухающих колебаний контура, когда его сопротивление равно нулю, определяется по формуле английского физика Томсона:
Период колебаний в реальном контуре напрямую зависит от его сопротивления R. Чем больше сопротивление R закрытого колебательного контура, тем больше период его колебаний.
Слайд 17
Параметры гармонических колебаний.
Пр. математики:
4. Величина обратная периоду называется
частотой колебания.
- частота колебания.
Пр. физики:
Частоту свободных колебаний, возникающих в замкнутом колебательном контуре, называют собственной частотой колебательной системы.
Частота собственных незатухающих колебаний контура вычисляется по формуле:
Слайд 18
Первичная проверка понимания и обсуждение результата.
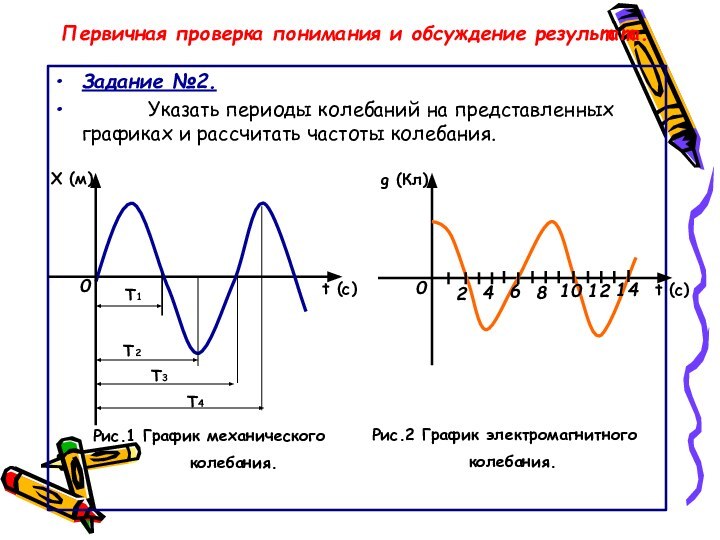
Задание №2.
Указать периоды колебаний на представленных графиках и
рассчитать частоты колебания.
Рис.1 График механического
колебания.
Х (м)
t (c)
Т1
Т2
Т3
Т4
t (c)
0
0
Рис.2 График электромагнитного
колебания.
g (Кл)
2
4
6
8
10
12
14
Слайд 19
Изучение нового материала.
Пр. математики: Из курса математики
известно, что наименьшим периодом функции косинуса и синуса является
величина 2П.
5. Если рассматривать число колебаний не за 1с, а за 2Пс, то полученную частоту называют циклической или круговой частотой.
- циклическая или круговая частота колебаний
Пр. физики:Циклическая частота колебаний для закрытого колебательного контура вычисляется по формуле:
Слайд 20
Пр. математики:
6. Выражениение, которое стоит под знаком синуса
или косинуса в уравнении гармонического колебания, называется фазой колебания.
φ [рад]- фаза колебания
Значение фазы в момент времени, равной нулю, называют начальной фазой колебания.
φ0 [рад] – начальная фаза колебания.
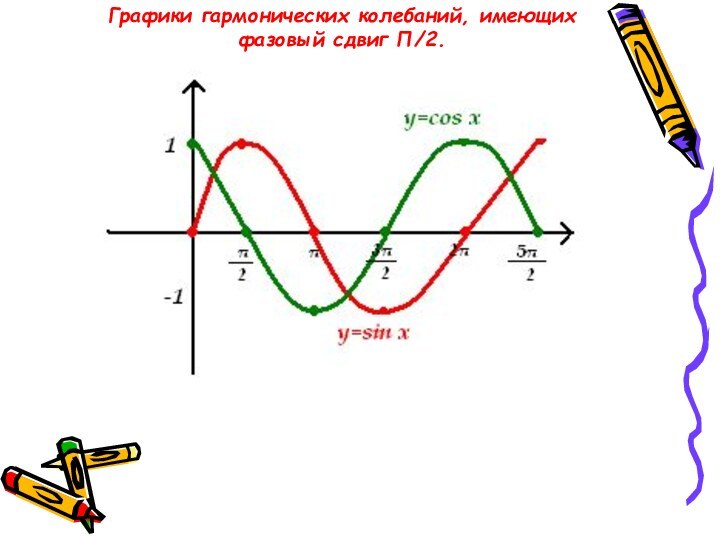
Функции у = cosx и у=sinx отличаются друг от друга фазами колебаний
cosφ = sin(φ + π/2)
Разность между фазами колеблющихся величин называют фазовым сдвигом.
∆φ = φ2 - φ1 [рад]
.
Слайд 21
Пример расчета разности фаз.
Уравнение изменения заряда
конденсатора по закону косинуса:
Уравнение изменения
заряда конденсатора по закону синуса:
Фазовый сдвиг между уравнениями:
Слайд 22
Графики гармонических колебаний, имеющих фазовый сдвиг П/2.
Слайд 25
Подведение итогов занятия.
Пр. физики.
У студентов сформировалось понятие электромагнитного
гармонического колебания, они убедилась в наличии математического обоснования данного
процесса, уяснили сущность параметров гармонических колебаний и способы вычисления их математическим и физическим путем , они смогли полученные знания использовали при выполнении проверочного задания. Запись конспекта занятия проводилась в рабочие тетради студентов, они проявляли инициативу при работе, так как заинтересованы в ее результатах.