- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Интерференция света
Содержание
- 2. Интерференция света Интерференция света – нелинейное сложение
- 3. Интерференция двух плоских волн Пусть имеются две
- 4. Случай неравных частот В некоторых учебниках и
- 5. Условия наблюдения интерференцииУсловия наблюдения интерференцииРассмотрим несколько характерных
- 7. Общий случай интерференции При взятии интеграла в
- 8. Скачать презентацию
- 9. Похожие презентации
Интерференция света Интерференция света – нелинейное сложение интенсивностей двух или нескольких световых волн. Это явление сопровождается чередующимися в пространстве максимумами и минимумами интенсивности. Ее распределение называется интерференционной картиной. Впервые явление интерференции было независимо обнаружено Робертом Бойлем





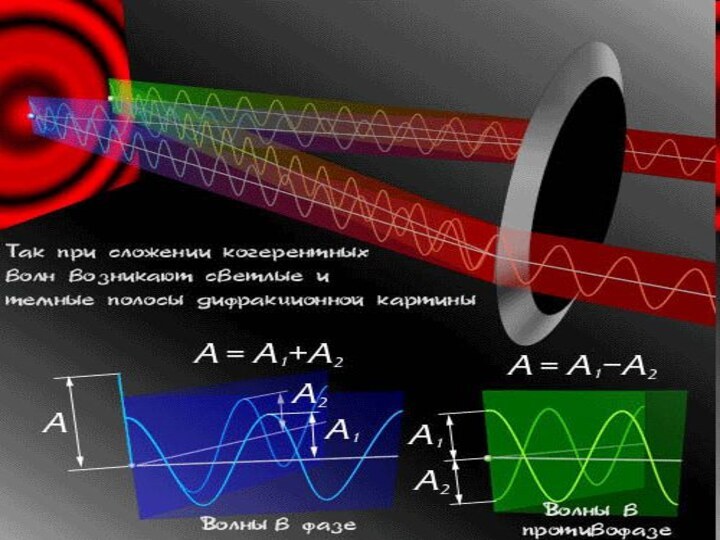


Слайд 3
Интерференция двух плоских волн
Пусть имеются две плоские волны:
и По принципу суперпозиции результирующее поле в области
пересечения этих волн будет определяться суммой:Интенсивность задается соотношением:
Откуда с учетом: :
Для простоты рассмотрим одномерный случай и сонаправленность поляризаций волн, тогда выражение для интенсивности можно переписать в более простом виде:
Интерференционная картина представляет собой чередование светлых и темных полос, шаг которых равен: Примером этого случая является интерференционная картина в отраженном от поверхностей плоско-параллельной пластинки свете.
Слайд 4
Случай неравных частот
В некоторых учебниках и пособиях говорится
о том, что интерференция света возможна только для волн
образованных от одного источника света путем амплитудного либо полевого деления волновых фронтов. Это утверждение является не верным. С точки зрения принципа суперпозиции интерференция существует всегда, даже когда интерферируют волны от двух разных источников света. Правильно было бы говорить о наблюдении или возможности наблюдения интерференционной картины. Последняя может быть нестационарна во времени, что приводит к замазыванию и исчезновению интерференционных полос. Рассмотрим две плоские волны с разными частотами:и По принципу суперпозиции результирующее поле в области пересечения этих волн будет определяться суммой:
Пусть некоторый прибор, обладающий некоторым характерным временем регистрации (экспозиции), фотографирует интерференционную картину. В физической оптике интенсивностью называют усредненный по времени поток световой энергии через единичную площадку ортогональную направлению распространения волны. Время усреднения определяется временем интегрирования фотоприемника, а для устройств, работающих в режиме накопления сигнала (фотокамеры, фотопленка и т. п.), временем экспозиции. Поэтому приемники излучения оптического диапазона реагируют на среднее значение потока энергии. Т. е. сигнал с фотоприемника пропорционален:
где под <> подразумевается усреднение. Во многих научно технических приложениях данное понятие обобщается на любые, в том числе и не плоские волны. Так как в большенстве случаев, например в задачах связанных с интерференцией и дифракцией света, исследуется в основном пространственное положение максимумов и минимумов и их относительная интенсивность, постоянные множители, не зависящие от пространственных координат, часто не учитываются. По этой причине часто полагают:
Квадрат модуля амплитуды задается соотношением:
Откуда, подставляя напряженность электрического поля, получим:
, где , , С учетом определения интенсивности можно перейти к следующиму выражению:
*, где - интенсивности волн Взятие интеграла по времени и применение формулы разности синусов дает следующие выражения для распределения интенсивности: В итоговом соотношении слагаемое, содержащее тригонометрические множители, называется интерференционным членом. Оно отвечает за модуляцию интенсивности интерференционными полосами. Степень различимости полос на фоне средней интенсивности называется видностью или контрастом интерференционных полос:
Слайд 5
Условия наблюдения интерференции
Условия наблюдения интерференции
Рассмотрим несколько характерных случаев:
1.
Ортогональность поляризаций волн.
При этом и . Интерференционные полосы отсутствуют,
а контраст равен 0. Далее, без потери общности, можно положить, что поляризации волн одинаковы.2. В случае равенства частот волн и контраст полос не зависит от времени экспозиции .
3. В случае значение функции и интерференционная картина не наблюдается. Контраст полос, как и в случае ортогональных поляризаций, равен 0
4. В случае контраст полос существенным образом зависит от разности частот и времени экспозиции.
Слайд 7
Общий случай интерференции
При взятии интеграла в соотношении ↑
полагалось, что разность фаз не зависит от времени. Реальные
же источники света излучают с постоянной фазой лишь в течение некоторого характерного времени, называемого временем когерентности. По этой причине, при рассмотрении вопросов интерференции оперируют понятием когерентности волн. Волны называют когерентными, если разность фаз этих волн не зависит от времени. В общем случае говорят, что волны частично когерентны. При этом поскольку существует некоторая зависимость от времени, интерференционная картина изменяется во времени, что приводит к ухудшению контраста либо к исчезновению полос вовсе. При этом в рассмотрении задачи интерференции, вообще говоря и не монохроматическгого (полихроматического) излучения, вводят понятие комплексной степени когерентности . Интерференционное соотношение принимает видОно называется общим законом интерференции стационарных оптических полей.





























