Слайд 2
Оглавление
Краткая биография стр.3
Формулировки стр.4-7
Формулы 8-11
Галерея
Слайд 3
Перед рассказом про законы Кеплера, хотелось бы рассказать

про их создателя Йоганна Кеплера.
Иоганн Кеплер
немецкий математик, астроном, механик,
оптик и астролог, первооткрыватель законов движения планет Солнечной системы и просто молодец.
Родился в 27 декабря 1571 года, Вейль-дер-Штадт.
Интерес к астрономии появился у Кеплера ещё в детские годы, когда его мать показала впечатлительному мальчику яркую комету (1577), а позднее — лунное затмение (1580).
Первоначально Кеплер планировал стать протестантским священником, но благодаря незаурядным математическим способностям был приглашён в 1594 году читать лекции по математике в университете города Граца.
Так начался путь Кеплера, как ученого.
Кеплер выпустил около 15 книг по астрономии. Несомненно Кеплер вложил большой вклад в развитие астрономии как XVI века, так и нынешней, ибо его законы лежат в основе многих теорий.
Благодаря исследованиям Кеплера, ученый Бонавентура Кавальери разработал «Метод Неделимых». Завершением этого процесса стало открытие математического анализа.
15 ноября 1630 года Йоганн Кеплер умирает в городе Регенсбург от простуды.
Слайд 4
Законы Кеплера
Законы Кеплера — три эмпирических соотношения, интуитивно
подобранных Иоганном Кеплером на основе анализа астрономических наблюдений Тихо
Браге.
Описывают идеализированную гелиоцентрическую орбиту планеты. В рамках классической механики выводятся из решения задачи двух тел предельным переходом / → 0, где , — массы планеты и Солнца соответственно.
Законы были открыты в конце 16 века, когда шла борьба между геоцентрической системой Птолемея и гелиоцентрической системой Коперника.
Слайд 5
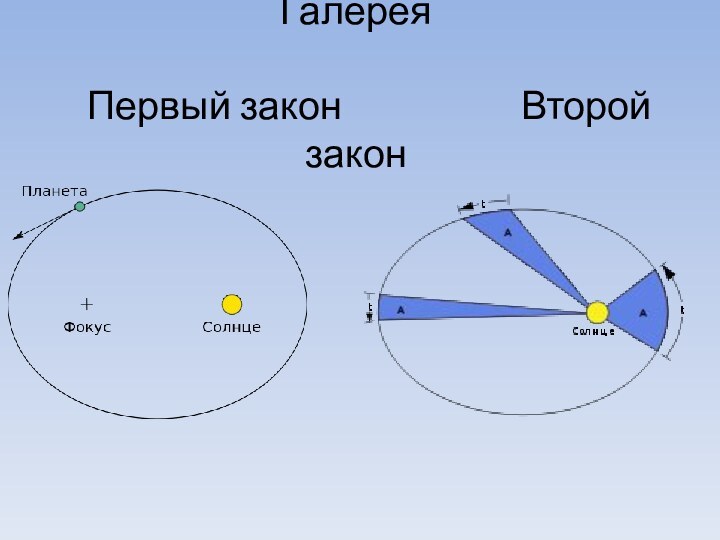
1-й закон Кеплера
«Каждая планета Солнечной системы обращается по
эллипсу, в одном из фокусов которого находится Солнце»
Форма эллипса
и степень его сходства с окружностью характеризуется отношением е=с/а , где с — расстояние от центра эллипса до его фокуса (половина межфокусного расстояния), а — большая полуось. Величина называется эксцентриситемом эллипса. При с=0, и, следовательно е=0 , эллипс превращается в окружность.
Слайд 6
2-й закон Кеплера(закон площадей)
«Каждая планета движется в плоскости,
проходящей через центр Солнца, причём за равные промежутки времени
радиус-вектор, соединяющий Солнце и планету, описывает равные площади»
Применительно к нашей Солнечной системе, с этим законом связаны два понятия: перигелий— ближайшая к Солнцу точка орбиты, и афелий — наиболее удалённая точка орбиты. Таким образом, из второго закона Кеплера следует, что планета движется вокруг Солнца неравномерно, имея в перигелии большую линейную скорость, чем в афелии.
Каждый год в начале января Земля, проходя через перигелий, движется быстрее, поэтому видимое перемещение Солнца по эклиптике к востоку также происходит быстрее, чем в среднем за год. В начале июля Земля, проходя афелий, движется медленнее, поэтому и перемещение Солнца по эклиптике замедляется. Закон площадей указывает, что сила, управляющая орбитальным движением планет, направлена к Солнцу.
Слайд 7
Третий закон Кеплера (гармонический закон)
«Квадраты периодов обращения планет
вокруг Солнца относятся, как кубы больших полуосей орбит планет»
Справедливо не только
для планет, но и для их спутников. Ньютон установил, что грав. притяжение планеты определенной массы зависит только от расстояния до неё, а не от других свойств, таких, как состав или температура. Он показал также, что третий закон Кеплера не совсем точен — в действительности в него входит и масса планеты.
Поскольку движение и масса оказались связаны, эту комбинацию гармонического закона Кеплера и закона тяготения Ньютона используют для определения массы планет и спутников, если известны их орбиты и орбитальные периоды.
Слайд 8
Формулы к законам Кеплера
Первый закон:
е=с\а – расстояние от центра до эллипса.
Слайд 9
2-й закон
По определению угловой момент L точечной частицы с массой
m и скоростью v записывается в виде:
.где r — радиус-вектор частицы а p=mv — импульс частицы.
Площадь, заметаемая радиус-вектором r за время dt из геометрических соображений равна , где представляет собой угол между направлениями и .
По определению
.В результате мы имеем
.Продифференцируем обе части уравнения по времени
поскольку векторное произведение параллельных векторов равно нулю. Заметим, что F всегда параллелен r, поскольку сила радиальная, и p всегда параллелен v по определению. Таким образом можно утверждать, что |L|, а следовательно и пропорциональная ей скорость заметания площади ds\dt — константа.
Слайд 10
2-ой закон Кеплера
Второй закон Кеплера утверждает, что радиус-вектор
обращающегося тела заметает равные площади за равные промежутки времени.
Если теперь мы возьмём очень малые промежутки времени в момент, когда планета находится в точках A и B (перигелий и афелий), то мы сможем аппроксимировать площадь треугольниками с высотами, равными расстоянию от планеты до Солнца, и основанием, равным произведению скорости планеты на время.
, где
Т1 и Т2 - периоды обращения двух планет вокруг Солнца, а а1 и а2 — длины больших полуосей их орбит.
Третий закон Кеплера не совсем точен — в действительности в него входит и масса планеты: ,где М-масса солнца, а м1 и м2- массы планет