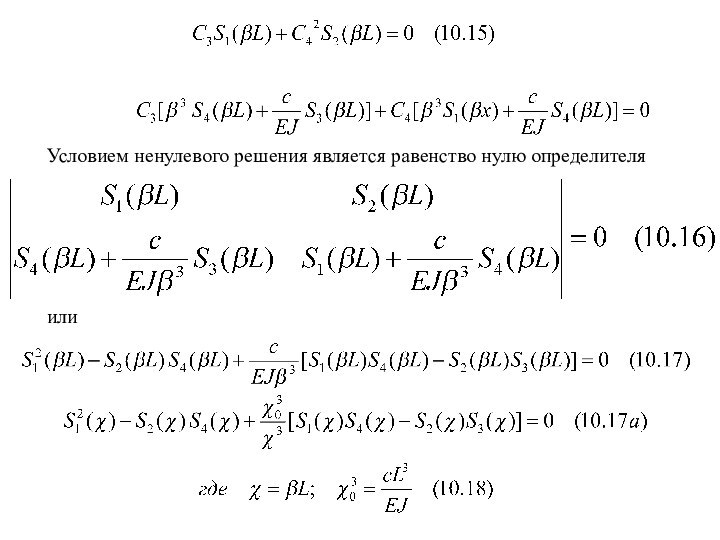при p = 0
Если стержень имеет постоянные по длине
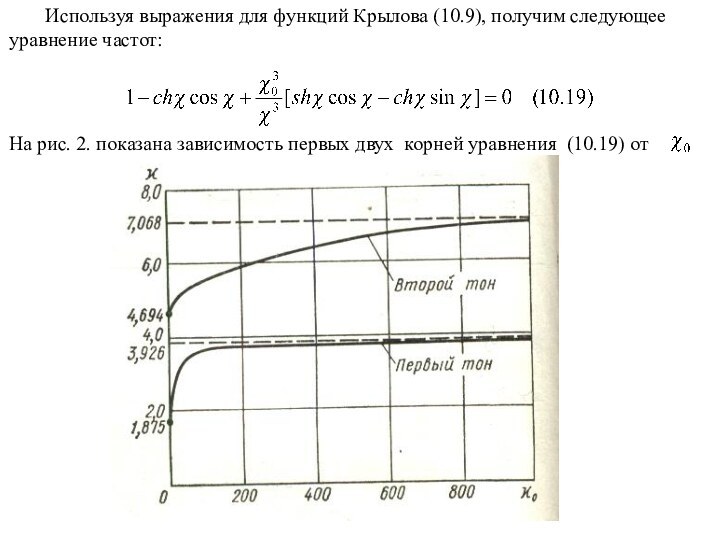
характеристики EJ = const, рF = const, то уравнение для исследования собственных колебаний будет следующим:
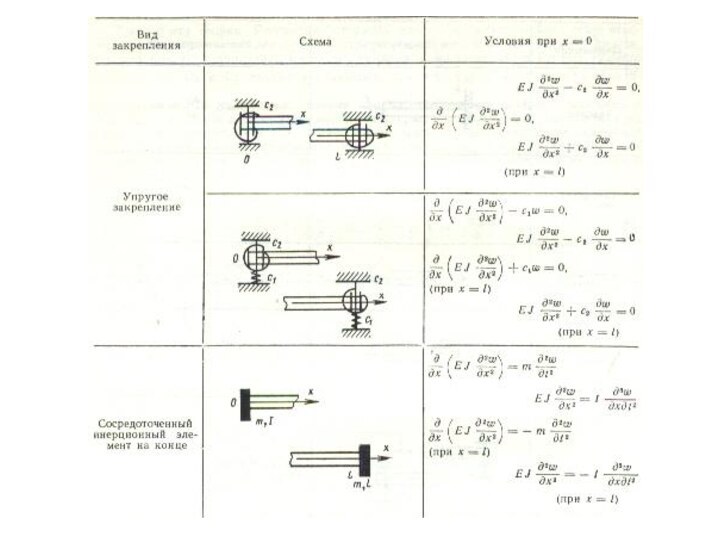
Функция w(x, t) на концах стержня должна удовлетворять краевым условиям, соответствующим характеру закрепления концов стержня.