Слайд 2
Задачи урока:
Образовательная:
формирование понятий: математический маятник, период колебаний
математического маятника;
экспериментальным путем установить законы колебаний математического маятника.
рассмотреть причины
и особенности колебаний математического маятника.
Воспитательная:
ориентировать учащихся на выбор профессии, поддерживать интерес к предмету.
применение математических маятников в разных сферах.
Развивающая:
содействовать формированию навыков сравнения, выделения главного и второстепенного в изучаемом материале, обобщения, логического мышления;
формировать экспериментальные навыки и умения.
Слайд 3
План урока:
Оргмомент.
Актуализация знаний по теме, мотивация учащихся на
изучение новой темы.
Изучение нового материала.
Решение экспериментальных задач по теме
(включая компьютерный эксперимент).
Итоги урока.
Домашнее задание.
Слайд 4
Любое ли тело может совершать колебательные движения? Что
для этого необходимо?
Слайд 5
Иллюстрация механических колебаний на примере маятника Фуко
После
просмотра телепередачи о архитектурных достопримечательностях Санкт – Петербурга и
находящегося в Исаакиевском соборе маятника Фуко, я очень заинтересовался этим уникальным устройством. Маятник Фуко служит для демонстрации вращения Земли вокруг своей оси. Его изобретение приписывают Ж.Фуко.
Слайд 6
Вначале опыт был выполнен в узком кругу, но
так заинтересовал Наполеона III, французского императора, что он предложил
Фуко повторить его публично в грандиозном масштабе под куполом Пантеона в Париже. Эту публичную демонстрацию, устроенную в 1851 году, и принято называть опытом Фуко.
Слайд 7
Эксперимент 1
Проделаем следующий опыт. Привяжем к карандашу нитку
с небольшим грузиком. Положив на стол линейку и, держа
карандаш горизонтально, подтолкнем маятник, чтобы он качался вдоль линейки. Постепенно поворачивая карандаш в горизонтальной плоскости, убедимся, что поворот карандаша не повлияет на маятник, он будет по-прежнему качаться вдоль линейки. Во время этого опыта не должно быть ветра, сквозняка, которые могли бы оказать влияние на колебания .
Слайд 8
Эксперимент 2
А теперь я предлагаю сделать другую модель
маятника Фуко. Перевернём вверх ногами табуретку и укрепим на
концах её ножек, по диагонали, деревянную палку, а к середине её привяжем маятник. Заставим его качаться так, чтобы плоскость его качания проходила между ножек табуретки вокруг его вертикальной оси. Медленно поворачивая табуретку вокруг её вертикальной оси, заметим, что теперь маятник качается уже в другом направлении. На самом деле он качается всё также, а изменение произошло из-за поворота самой табуретки, которая в данном опыте играет роль нашей Земли.
Слайд 9
Математический маятник
Смотри учебник физики Н. С. Пурышевой, Н.
Е. Важеевской и В. М. Чаругина стр. 105
Математическим маятником
называют тело, подвешенное на нити, размеры которого много меньше длины нити.
Слайд 10
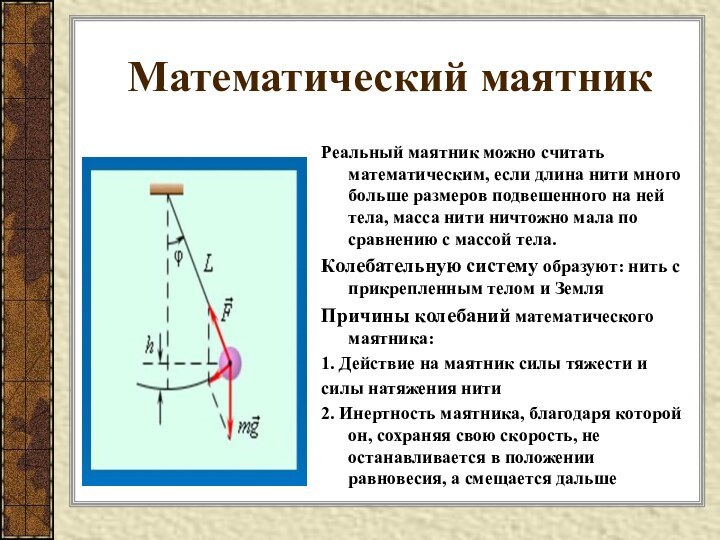
Математический маятник
Реальный маятник можно считать математическим, если длина
нити много больше размеров подвешенного на ней тела, масса
нити ничтожно мала по сравнению с массой тела.
Колебательную систему образуют: нить с прикрепленным телом и Земля
Причины колебаний математического маятника:
1. Действие на маятник силы тяжести и
силы натяжения нити
2. Инертность маятника, благодаря которой он, сохраняя свою скорость, не останавливается в положении равновесия, а смещается дальше
Слайд 11
Галилео Галилей
(1564-1642)
Великий итальянский ученый – один из создателей
точного естествознания.
Родился в городе Пизе, известном своей наклонной башней.
Учился сначала в монастырской школе, а затем в университете. Уже в студенческие годы Галилей увлекся изучением колебаний. Он обнаружил, что колебания маятника не зависят от его массы, а определяются длиной подвеса.
Слайд 12
Сохранилось предание о том, как молодой студент медицинского
факультета Галилео Галилей в одно из воскресений 1583 года
с интересом следил за качаниями зажженных лампад в церкви. По ударам пульса он определил время, необходимое для полного размаха лампад. С этого времени медицину пришлось ему оставить и сосредоточиться на физике.
Старое здание Пизанского университета
Слайд 13
Работа в группах
Задание 1 группе:
Выяснить опытным путем,
зависит ли период колебания математического маятника от его массы.
Задание
2 группе:
Выяснить, зависит ли период колебания маятника от длины маятника.
Слайд 14
Выводы:
Группа 1: Период колебаний математического маятника не зависит
от массы шарика.
Группа 2: Период колебаний математического маятника зависит
от его длины, с увеличением длины возрастает период.
Слайд 15
Общий вывод:
Период колебания математического маятника прямо пропорционален длине
маятника и обратно пропорционален ускорению свободного падения.
Слайд 16
Компьютерная модель математического маятника, созданная с использованием программы
Macromedia Flash 5.
Слайд 17
Гюйгенс Христиан (1629 – 1695)
Формула периода колебаний математического
маятника впервые была получена на опыте голландским ученым Х.
Гюйгенсом, современником И. Ньютона.
Слайд 18
В 1656 году в возрасте 27 лет Гюйгенсом
были сконструированы первые маятниковые часы со спусковым механизмом. Создание
часов, измеряющих время с невиданной точностью, имело далеко идущие последствия для развития физического эксперимента и практической деятельности человека. До этого, время измеряли по истечению воды, горению факела или свечи.
Слайд 19
А как выяснить зависимость периода колебания от ускорения
свободного падения?
Можно искусственно увеличить тяготение к Земле, но мы
это не можем. Самое простое – добавить к силе тяготения другую силу, например, магнитную, для чего поместим под маятник электромагнит.
Эти силы сообщат маятнику ускорение больше, чем ускорение свободного падения, что приведет к изменению периода колебаний.
Слайд 21
Практическое использование колебаний маятника
Ускорение свободного падения меняется с
географической широтой, так как плотность земной коры различна. В
районах, где залегают плотные породы, ускорение несколько больше. Прибор с маятником применили для разведки полезных ископаемых. Подсчитав число качаний, можно обнаружить в земных недрах руды или уголь. Они обладают повышенной плотностью по сравнению с обычными породами и всегда тяжелее лежащих под ними более рыхлых горных пород.
Слайд 22
Это интересно…
О маятнике, его роли и влиянии на
жизнь и судьбу человека, писали многие философы и великие
ученые: Аристотель, Плутарх, Платон, Сократ, Архимед. Последний использовал маятник при вычислениях.
С помощью маятника однажды удалось отыскать пропавшего ребенка. Это произошло в 1934 году. Малыша на глазах у многих свидетелей унес орел.
После того как полицией были предприняты безуспешные попытки отыскать его, было решено прибегнуть к помощи маятника, который стали раскачивать над картой, и в том месте, где амплитуда его колебаний достигла максимальной силы, было решено искать ребенка. К удивлению многих, именно там и оказался пропавший мальчик. Эти сенсационные факты были опубликованы в швейцарской газете «Трибюн де Женев».
Слайд 23
Это интересно…
Известный французский естествоиспытатель и астроном К. Фламмарион
в своих исследованиях также часто пользовался маятником. С его
помощью ученый предсказал падение Тунгусского метеорита, открытие новой планеты, движение комет.
А в Берлине в период Второй мировой войны существовал даже специальный институт маятника. Ныне тем же самым, но только на более высоком уровне, занимается Мюнхенский институт парапсихологии. Работу с маятником здесь окрестили «радиэстезией».
Слайд 24
Сегодня на уроке я:(поставить «+» или « -
»)
-дополнял ответы других учеников
- работал самостоятельно в тетради
-
выполнял задания
- участвовал в обсуждении проблемы
- доказывал свою точку зрения
За урок я бы себе поставил оценку………….
Над чем мне надо работать, чтобы улучшить свои знания?