- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Механические колебания (11 класс)
Содержание
- 2. Механические колебания – это движение, которые повторяются
- 3. Колебательные системы.Примеры колебаний, изображенные на рисунках: колебания
- 4. Условия возникновения механических колебанийНаличие положения устойчивого равновесия,
- 5. Превращение энергии при колебательном движенииmgE=0; v=0E=Eпmaxv=vmaxE=EкmaxE= Eк+
- 6. Параметры колебательного движения1. Смещение х - отклонение
- 7. Гармонические колебанияКолебания, при которых изменения физических величин
- 8. Скорость при гармонических колебаниях. Согласно определению скорости,
- 9. Ускорение при гармонических колебанияхУскорение – это производная
- 10. Свободные колебания математического маятникаМатематический маятник- модель –
- 11. Период колебанияСравним полученное уравнение с уравнением колебательного
- 12. Свободные колебания пружинного маятникаТогда согласно второму законуНьютона,
- 13. Период колебанияТ.к.Сравним полученное уравнение с уравнением колебательного
- 15. Основные понятияВибратор – колеблющееся тело, источник волны.
- 16. Поперечная волна
- 17. Скачать презентацию
- 18. Похожие презентации














Слайд 2 Механические колебания – это движение, которые повторяются через
определенные интервалы времени.
периодически изменяющейся силы.
Слайд 3
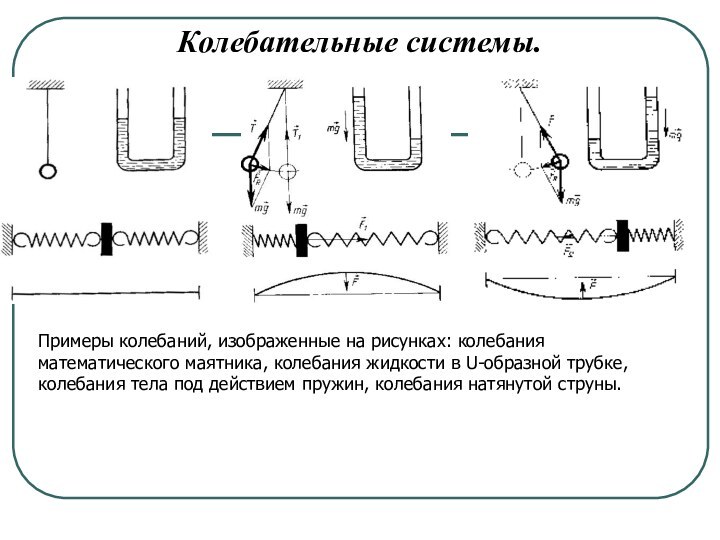
Колебательные системы.
Примеры колебаний, изображенные на рисунках: колебания математического
маятника, колебания жидкости в U-образной трубке, колебания тела под
действием пружин, колебания натянутой струны.
Слайд 4
Условия возникновения механических колебаний
Наличие положения устойчивого равновесия, при
котором равнодействующая равна нулю
Хотя бы одна зависит от координат
Наличие
в колеблющейся материальной точке, избыточной энергииЕсли вывести тело из положения равновесия, то равнодействующая не равна нулю
Сила трения в системе малы
Для возникновения колебания тело необходимо вывести из положения равновесия, сообщив либо кинетическую энергию (удар, толчок), либо – потенциальную (отклонение тела).
Примеры колебательных систем:
1. Нить, груз, Земля.
2. Пружина, груз.
3. Жидкость в U-образной трубке, Земля.
4. Струна.
Слайд 5
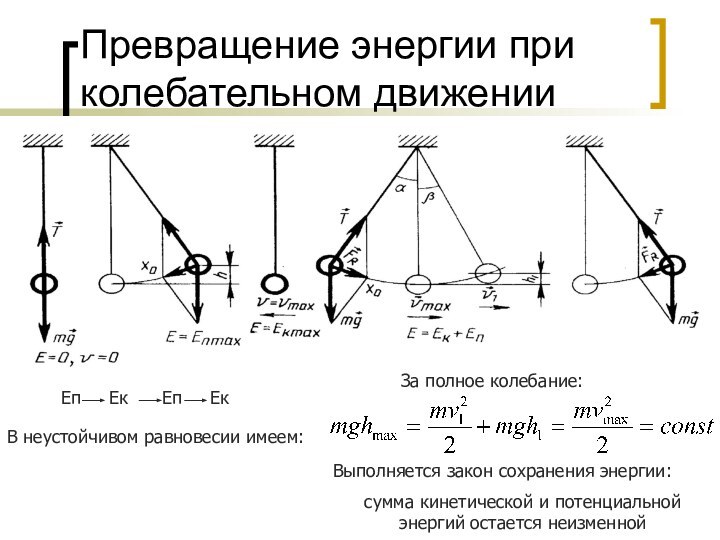
Превращение энергии при колебательном движении
mg
E=0; v=0
E=Eпmax
v=vmax
E=Eкmax
E= Eк+ Eп
В
неустойчивом равновесии имеем:
Eп Eк Eп
EкЗа полное колебание:
Выполняется закон сохранения энергии:
сумма кинетической и потенциальной энергий остается неизменной
Слайд 6
Параметры колебательного движения
1. Смещение х - отклонение колеблющейся
точки от положения равновесия в данный момент времени (м).
2.
Амплитуда хмax - наибольшее смещение от положения равновесия (м). Если колебания незатухающие, то амплитуда постоянна.3. Период Т — время, за которое совершается одно полное колебание. Выражается в секундах (с).
4. Частота — число полных колебаний за единицу времени. В СИ измеряется в герцах (Гц).Частота колебаний равна одному герцу, если за 1 секунду совершается 1 полное колебание. 1 Гц= 1 с-1.
5. Циклической (круговой) частотой периодических колебаний наз. число полных колебаний, которые совершаются за 2 единиц времени (секунд).
Единица измерения – с-1.
6. Фаза колебания - - физическая величина, определяющая смещение x в данный момент времени. Измеряется в радианах (рад).Фаза колебания в начальный момент времени (t=0) называется начальной фазой (0).
Слайд 7
Гармонические колебания
Колебания, при которых изменения физических величин происходят
по закону косинуса или синуса
Выражение, стоящее под знаком
cos или sin, наз. фазой колебания: Фаза колебания измеряется в радианах и определяет значение смещения (колеблющейся величины) в данный момент времени.
Амплитуда колебания зависит только от начального отклонения
Слайд 8
Скорость при гармонических колебаниях.
Согласно определению скорости, скорость
– это производная от координаты по времени
Таким образом,
мы видим, что скорость при гармоническом колебательном движении также изменяется по гармоническому закону, но колебания скорости опережают колебания смещения по фазе на /2. Величина - максимальная скорость колебательного движения (амплитуда колебаний скорости).
Следовательно, для скорости при
гармоническом колебании имеем:
Слайд 9
Ускорение при гармонических колебаниях
Ускорение – это производная от
скорости по времени:
Тогда:
Ускорение при гармоническом колебательном движении также
изменяется по гармоническому закону, но колебания ускорения опережают колебания скорости на /2 и колебания смещения на (говорят, что колебания происходят в противофазе). Величина
- максимальное ускорение
- вторая производная смещения прямо пропорциональна (с противоположным знаком) смещению. Такое уравнение наз. уравнением гармонического колебания
Слайд 10
Свободные колебания математического маятника
Математический маятник- модель – материальная
точка, подвешенная на нерастяжимой невесомой нити.
Выведем маятник из положения
равновесия:Т.к. мал, то
отсюда:
Ускорение материальной точки математического маятника пропорциональна смещению S
Слайд 11
Период колебания
Сравним полученное уравнение
с уравнением колебательного движения
Видно, что
или
- циклическая частота при колебаниях математического
маятника. Период колебаний
или
Период колебаний математического маятника не зависит от массы тела!
Слайд 12
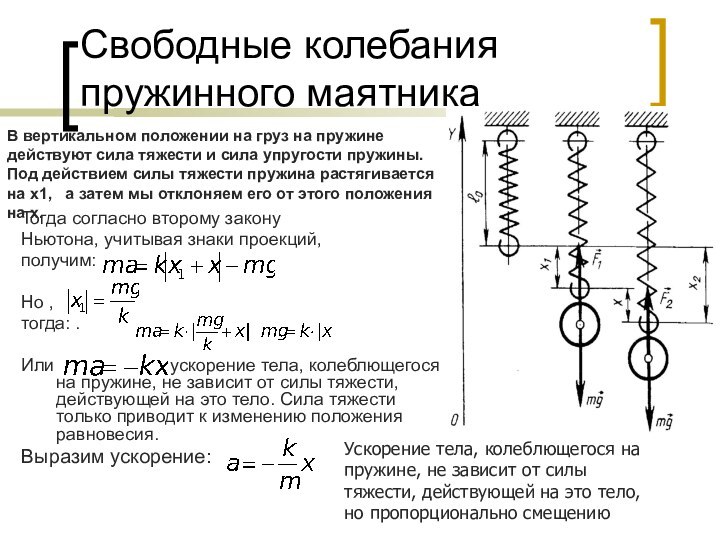
Свободные колебания пружинного маятника
Тогда согласно второму закону
Ньютона, учитывая
знаки проекций,
получим:
Но ,
тогда: .
Или
- ускорение тела, колеблющегося на пружине, не зависит от силы тяжести, действующей на это тело. Сила тяжести только приводит к изменению положения равновесия. Выразим ускорение:
В вертикальном положении на груз на пружине действуют сила тяжести и сила упругости пружины. Под действием силы тяжести пружина растягивается на х1, а затем мы отклоняем его от этого положения на х.
Ускорение тела, колеблющегося на пружине, не зависит от силы тяжести, действующей на это тело, но пропорционально смещению
Слайд 13
Период колебания
Т.к.
Сравним полученное уравнение с уравнением колебательного движения
.
Видно, что
или
- циклическая частота при колебаниях
пружинного маятника. Период колебаний
или