Презентация на тему Оболочечная модель ядра

удерживающих протоны и нейтроны внутри ядра. Общей теории ядерных

сил до сих пор не создано. Экспериментальные данные указывают на отдельные свойства ядерных сил. Часто свойства оказываются противоречивыми, чтобы создать одну модель, учитывающую все характеристики взаимодействия внутри ядра.

Свойства ядерных сил

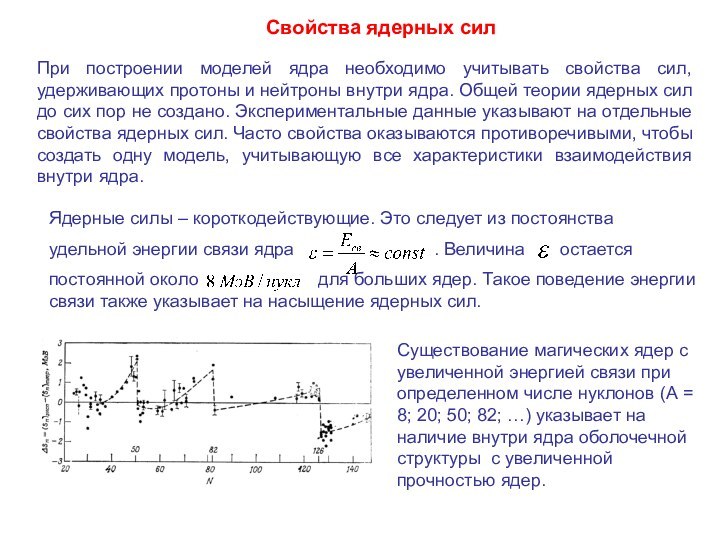
Ядерные силы – короткодействующие. Это следует из постоянства
удельной энергии связи ядра . Величина остается
постоянной около для больших ядер. Такое поведение энергии связи также указывает на насыщение ядерных сил.

Существование магических ядер с увеличенной энергией связи при определенном числе нуклонов (А = 8; 20; 50; 82; …) указывает на наличие внутри ядра оболочечной структуры с увеличенной прочностью ядер.

энергия связи двух нуклонов

за

счет взаимодействия остается практически одинаковой, за вычетом поправки на кулоновское отталкивание.
На это указывает одинаковая структура уровней зеркальных ядер (число протонов одного ядра равно числу нейтронов другого ядра, при
одинаковом массовом числе А: ).

Внутри ядра происходит парное спаривание нуклонов с компенсацией динамических характеристик, таких как спины, магнитные моменты. Для самых тяжелых ядер суммарные моменты (спины) не превышают

Свойства ядерных сил

Ядерные силы имеют сложный тензорный характер (не центральный).

нуклонов. Оказывается, что

- при параллельном направлении спина и момента, энергия связи нуклона оказывается больше.
Ядерные силы носят локальный обменный характер. Переносчиком выступает виртуальный π-мезон с радиусом дальнодействия порядка 1 ферми (~1φ).
Существует симметрия между числом протонов и нейтронов.

Реально, с учетом кулоновского взаимодействия, уменьшающего внутреннюю энергию протонов, получается поднятие “дна” потенциала, что приводит к уменьшению числа протонов для стабильных ядер.

Плотность нуклонов внутри ядра остается практически постоянной – подобно состоянию капли вещества

Свойства ядерных сил

условно разделить на два класса: с сильной связью между

частицами и независимым движением частиц внутри ядра.
К первому классу относится капельная модель, с короткодействующим сильным взаимодействием частиц на маленьких расстояниях r по сравнению с размером самого ядра (r << Rяд). Пробег взаимодействия (L) частиц внутри ядра, также предполагается маленьким (L<< Rяд). Состояние нуклона определяется только нуклонами его ближайшего окружения.
Эта модель объясняют энергетические характеристики ядра: возможность распада, деления, устойчивость ядер, энергию связи и др.
В модели независимых частиц предполагается, что отдельные нуклоны свободно движутся (по оболочкам) в усредненном потенциальном поле, образованном всеми частицами ядра. Пробег взаимодействия частиц получается большим (L>>Rяд). Большой пробег частиц для низкого состояния по энергии обусловлен принципом Паули для фермионов.

Эта модель объясняет динамические характеристики ядра - спин ядра, четность энергетических уровней, магнитный момент.

по сравнению с близлежащими по массе ядрами) указывает на

существование в ядре внутренних замкнутых оболочек.

Модель должна объяснить правила заполнения оболочек, величину спина ядра и четность состояния ядра.

В основу оболочечной модели положены следующие предположения:
Нуклоны движутся по орбитам в центрально-симметричном силовом поле, образованном всеми нуклонами.

2. Для нуклонов существует спин-орбитальная связь, поэтому вектор момента нуклона J = L + S ведет себя как единое целое.

3. Нуклоны, как фермионы, характеризуются четырьмя квантовыми числами (n, L, j, mj). В центрально-симметричном полем существует вырождение энергетических уровней по проекции .

и четность ядра создаются последним непарным нуклоном
5. В простейшем

виде, для потенциала применяется
модель гармонического осциллятора:
6. Решение квантово-механических уравнений дает правило для положения уровней энергии (n0 = 0, 1, 2, 3…)
Уровни энергии получаются эквидистантными
7. Для правильного расположения уровней энергии вводится дополнительное расщепление за счет спин-орбитального взаимодействия отдельных нуклонов.
8. Энергия оказывается больше, если спин и орбитальный момент сонаправлены
Например, для n = 1 и L = 1 получим два вектора
Возникает два подуровня n L j :
первый из которых расположен глубже в потенциальной яме.

представлено заполнение уровней для двух вариантов моделей: без спин-орбитального

взаимодействия (без расщепления), с учетом взаимодействия – c расщеплением уровней.